The photon has a wave nature, which is why we can refract and diffract light. But what sort of a wave nature? When you try to find a picture, a lot of illustrations depict the photon as some kind of wave train. Even Feynman diagrams do this.
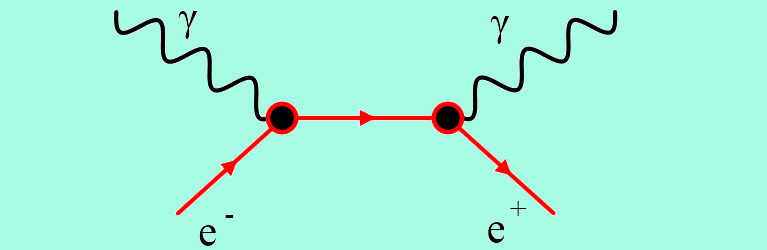 Image by bitwise, see Wikipedia commons
Image by bitwise, see Wikipedia commons
The photon is shown as a squiggly line, sometimes with an arrowhead, something like this: ⇝. That suggests you could split a photon lengthwise and end up with two photons, each with the same wavelength as the original, each with half the energy. That can’t be right. The photon energy E = hc/λ depends on Planck’s constant h and the wavelength lambda λ. Wavelength is inversely related to frequency f via the speed of light c, which is distance over time. Hence we can also write the photon energy as E = hf. But there is nothing in this expression to denote the number of waves in the train. And when you chop a photon in half with a beam splitter to convert it into two photons, each has twice the wavelength as the original. The photon is one of those things where when you chop it in half it’s twice as big. So it isn’t a wave train.
The photon is not a wave packet
Other illustrations depict the photon as a wave packet. You can find articles suggesting that Einstein talked about wave packets in his 1905 photoelectric paper. However he didn’t actually use the phrase, he talked about the light quantum instead. He said light quanta move without dividing and are absorbed or generated only as a whole, and that the simplest picture is one where the light quantum gives its entire energy to a single electron. That fits with the wave-packet idea. But Einstein also said “it must not be excluded that electrons accept the energy of light quanta only partially”. That’s as per Compton scattering, where some of the photon energy is transferred to an electron and the photon wavelength increases. That doesn’t fit with the wave-packet idea. And as far as we know the photon has a single wavelength, not multiple wavelengths. There is no actual evidence that a photon is some infinite set of component sinusoidal waves. On the contrary, the evidence says the photon is a single wave or pulse as per How Long Is a Photon? by Igor Drozdov and Alfons Stahlhofen dating from 2008. There are no observations of any oscillations inside a photon. There is no evidence that a photon is a wave-train like their figure1. Or a lemon-like wave-packet of waves of different amplitudes like figure 2. The evidence says the photon is more like their figure3:
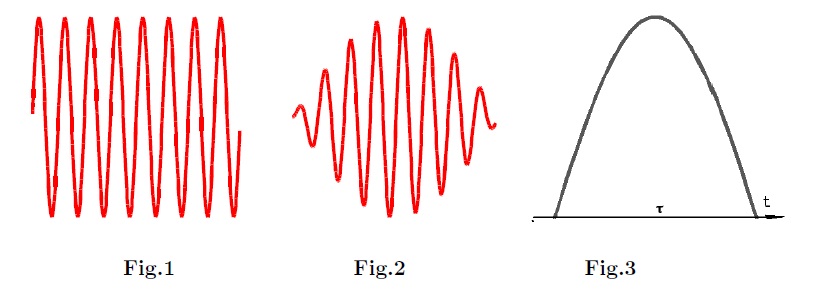 Images from How Long Is a Photon? by Igor Drozdov and Alfons Stahlhofen
Images from How Long Is a Photon? by Igor Drozdov and Alfons Stahlhofen
That’s not to say waves don’t come in trains. We know they do. We’ve seen what happens in an earthquake. But I think it’s better to say a train of light waves is a succession of photons, not a single photon. So I think the photon must be some kind of a singleton soliton light wave. So far so good.
The photon is not an electric wave and a magnetic wave
So, a photon is a singleton soliton light wave. Light waves are electromagnetic waves. Not electric waves and magnetic waves, electromagnetic waves. James Clerk Maxwell unified electricity and magnetism a hundred and fifty years ago. The electromagnetic field is a dual entity, wherein electric and magnetic fields are “better thought of as two parts of a greater whole”. See section 11.10 of John Jackson’s Classical Electrodynamics where he says “one should properly speak of the electromagnetic field Fµv rather than E or B separately”. It’s similar for electromagnetic waves. See the Wikipedia electromagnetic radiation article and note this: “the curl operator on one side of these equations results in first-order spatial derivatives of the wave solution, while the time-derivative on the other side of the equations, which gives the other field, is first order in time”. The orthogonal sinusoidal electric and magnetic waves in the depictions are somewhat misleading. The electric wave is the spatial derivative of a wave of electromagnetic potential, whilst the magnetic wave is the time derivative. For an analogy, imagine you’re in a canoe at sea. Imagine something like an oceanic swell wave or tsunami comes at you. Let’s say it’s a 10m high sinusoidal hump of water without a trough. As the wave approaches, your canoe tilts upward.
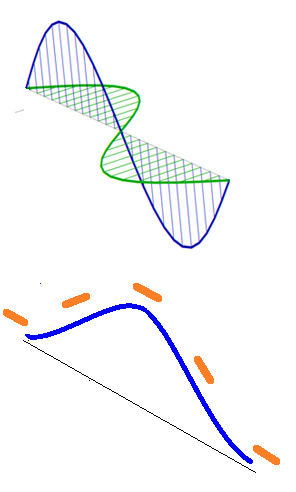 The canoe analogy, E= tilt, B=rate of change of tilt
The canoe analogy, E= tilt, B=rate of change of tilt
The degree of tilt denotes E, whilst the rate of change of tilt denotes B. When you’re momentarily at the top of the wave, your canoe is horizontal and has momentarily stopped tilting, so E and B are zero. Then as you go down the other side, the situation is reversed. The important point to note is that there’s only one wave there. Like Oleg Jefimenko said: “neither Maxwell’s equations nor their solutions indicate an existence of causal links between electric and magnetic fields. Therefore, we must conclude that an electromagnetic field is a dual entity always having an electric and a magnetic component simultaneously created by their common sources: time-variable electric charges and currents”. That’s why E and B are always in phase. Because the current in this canoe analogy is water surging up then down. It displaces you in an upward direction with a tilt and a rotation that increases then decreases. Then it displaces you back down again. Because of this It’s an alternating current rather than a direct current like a river. Note that electrical impedance is resistance to alternating current, and that there’s such a thing as wave impedance and vacuum impedance. Also note that it’s a myth that an E wave generates a B wave which generates an E wave and so on. The people who say this tend to be unaware of electromagnetic unification, and tend to say that this is why light doesn’t need a medium to travel in. It’s an incorrect assertion. We have Faraday’s law, usually written as ∇ × E = − ∂B/∂t, not because changing one field creates the other, or because one circulates round the other. The equals sign is an “is”. The curl of E is the time rate of change of B. Because they’re two aspects of the same thing, the electromagnetic wave.
Potential is more fundamental than field
Or they’re two aspects of an electromagnetic field-variation if you prefer. I prefer the former myself, because I think the photon electromagnetic wave is more fundamental than the electron electromagnetic field. But perhaps neither is ideal, because potential is said to be more fundamental than field. There’s an unattributed remark in the Wikipedia Aharonov-Bohm article: it says Feynman wished he’d been taught electromagnetism from the perspective of electromagnetic potential rather than electromagnetic fields. Yes, there’s an unfortunate ambiguity in that the use of the word fields as opposed to field suggests we’re talking about the electric field and the magnetic field, not the electromagnetic field. And things can get confusing in that electromagnetic four-potential is also described as the gauge field of quantum electrodynamics. But remember that as per the canoe analogy, the orthogonal sinusoidal electric and magnetic waves are the spatial and time derivatives of the real wave. The real wave is the integral of either sine wave. Now think of that hump of water, and the potential is the height of it. It’s there because the water is there. The electromagnetic wave is the exterior derivative of potential, the shape of the hump. The electric field is the slope of the hump at some point, and the magnetic field is the time-rate-of-change of slope. The important point is that without ten metres of extra water underneath you, there would be no hump, no slope, and no change of slope either. That’s why potential is more fundamental than field. However it can be difficult to detect. If you were canoeing on Lake Superior, you might not realise you’re 600ft above sea level. It tends to be a local change in potential that you can readily detect. Like at Niagara Falls.
The photon takes many paths
Mind you, it might not be quite as local as you might think. When you look at the sea, you see waves that are perhaps a metre high. It’s tempting to think that’s the size of them, but it isn’t. If you take a look at wind waves on Wikipedia, you can see what lies beneath. The wave isn’t something that’s a metre high. It extends deep into the ocean:
 GNUFDL image by Kraaiennest, see Wikipedia Commons
GNUFDL image by Kraaiennest, see Wikipedia Commons
If you could pick up the whole ocean and place it upside down on top of another ocean, you would appreciate that a wave running through it isn’t just a metre high. The displacement might be a metre in extent at its maximum, but the wave itself might be much more extensive. It’s similar with a shear wave in a solid. Think of a seismic S-wave travelling West to East from A to B across a plain. It isn’t just the houses sitting on top of the AB line that shake. Houses five miles north and south of the AB line shake, albeit less. Houses ten miles north or south shake too, albeit even less. People can still feel that earthquake a hundred miles away from the AB line. Seismometers can still detect it a thousand miles away. The point to note is that a seismic wave doesn’t just take the direct AB path like it’s some point-particle. Even if it goes straight as a die from A to B it effectively takes many paths. It’s similar for a photon, because it has a wave nature, and that’s what waves are like:
However electromagnetic waves aren’t exactly like water waves on the ocean. Water waves are also known as surface gravity waves, and they’re trochoidal rather than sinusoidal. In addition the speed of an ocean wave depends on wavelength, and the speed of an electromagnetic wave does not. An electromagnetic wave is more like the seismic S-wave in that the speed depends on the medium through which it moves, not on wavelength. But it isn’t exactly like the S-wave. As per Richard Beth’s 1936 paper on the mechanical detection and measurement of the angular momentum of light, the photon’s angular momentum is either ħ or -ħ depending on whether it has a left or right circular polarization. It’s orthogonal to the angular momentum of the trochoidal wave.
The quantum nature of light
See Leonard Susskind talking about Planck’s constant in the YouTube video demystifying the Higgs boson. At 2 minutes 50 seconds he rolls his whiteboard marker round saying angular momentum is quantized. Think like this: ”roll your marker round fast or slow, but roll it round the same circumference, because Planck’s constant of action h is common to all photons regardless of wavelength”. The quantum nature of light isn’t just some slope on a photoelectric graph. It’s something real. As for what, the dimensionality of action can be expressed as energy multiplied by time, or momentum multiplied by distance. As for what distance, take a look at some pictures of the electromagnetic spectrum. Note how the wave height is always the same regardless of wavelength:
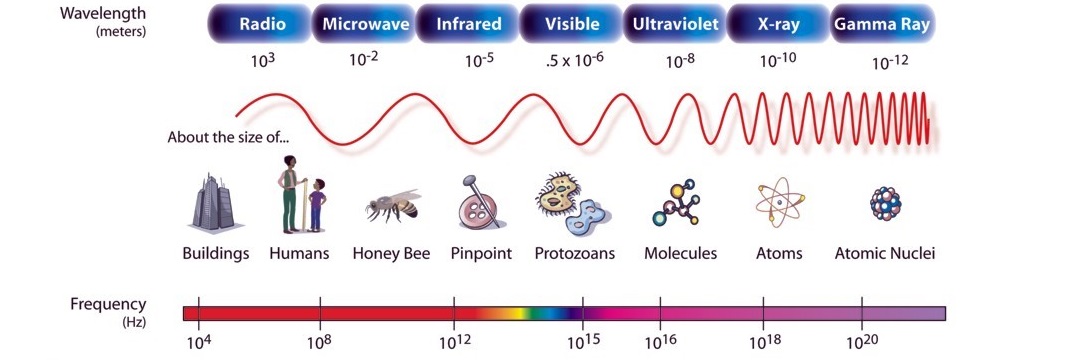 Electromagnetic spectrum image thanks to NASA
Electromagnetic spectrum image thanks to NASA
Yes, it’s only a picture, but I think it’s important, because I think the quantum nature of light is hiding in plain sight. It isn’t anything to do with energy being conveyed in lumps. A photon can have any frequency you like, and therefore any E = hf energy you like. You can vary the energy smoothly, so it isn’t anything to do with quantum lumps. It’s to do with this: the amplitude of all light waves is the same regardless of frequency. What amplitude? The answer to that depends on another question, which is this: what waves? To answer that, we need to ask another question: do you know of any waves where something doesn’t wave? Because I don’t.
Electromagnetic waves travel through space
Electromagnetic waves travel through space, which Einstein said was a something rather than a nothing. He is said to have dispensed with the luminiferous aether, but in his 1920 Leyden Address he referred to space as the ether of general relativity. See the Robert Laughlin quote in the Wikipedia aether theories article: “It is ironic that Einstein’s most creative work, the general theory of relativity, should boil down to conceptualizing space as a medium when his original premise [in special relativity] was that no such medium existed”. That might comes as a surprise, but remember what Cao and Schweber said about the plenum assumption of the bare vacuum – the vacuum isn’t some state of nothingness, it’s a polarizable medium. Hence Schwinger’s 1949 paper quantum electrodynamics II : vacuum polarization and self-energy. The speed of a shear wave is given as c = √(G/ρ), and the speed of a light wave is given as c = 1/√(ε0μ0). I do not believe this similarity is mere coincidence. Particularly since the Maxwell stress tensor is a part of the electromagnetic stress–energy tensor. Particularly since in his 1929 history of field theory Einstein described a field as a state of space. That might sound archaic, but see what Steven Weinberg said on page 25 of Dreams of a Final Theory: “a field like an electric or magnetic field is a sort of stress in space”. Also note that the stress-energy-momentum tensor “describes the density and flux of energy and momentum in spacetime”, and it includes a shear stress term. Shear stress is something that only a solid can sustain. Gases and liquids cannot, which is why there are no transverse waves in the air or the sea. So in a way, the stress-energy-momentum tensor treats space like some kind of gin-clear ghostly elastic solid. It’s not totally unlike the continuum-mechanics Cauchy stress tensor.
Space waves
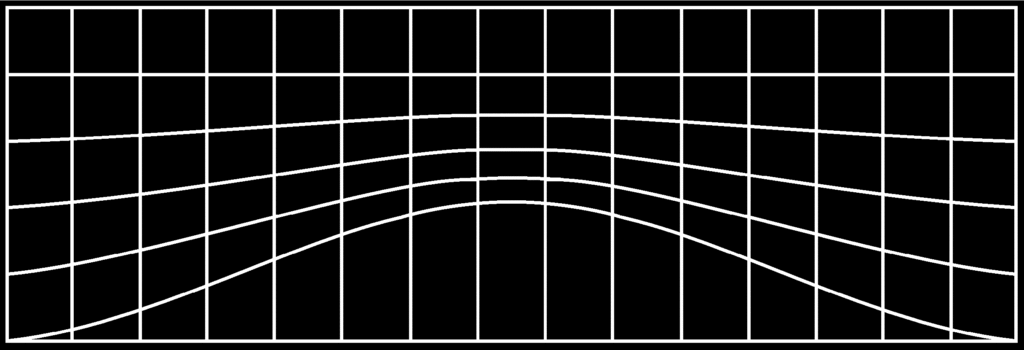
So, when we ask what waves, I think the answer is clear. After all, when an ocean wave moves through the sea, the sea waves. When a seismic wave moves through the ground, the ground waves. So, what waves when a light wave moves through space? There can only be one answer, and that answer must be space. Space waves. Some might dispute that, and say the electromagnetic field waves instead. But if you’ve ever read Einstein trying to unify the electromagnetic and gravitational field I think you would take a different view. Especially if you’ve also read LIGO articles which say “gravitational waves are ‘ripples’ in the fabric of space-time”. Then when you know that gravity is “not the curvature of space, but of spacetime”, you know that a gravitational field is not a place where space is curved. Instead it’s a place where space is inhomogeneous, in a non-linear way. It’s like a spatial-energy density-variation, and it must be the same for a gravitational wave but in a dynamical fashion. A gravitational wave is said to be a quadrupole wave, with alternate transverse and longitudinal compression. To keep it simple I’ll show only the latter:

It’s rather like a sound wave. The grid lines aren’t curved. Space isn’t curved where a gravitational field is, or where a gravitational wave is. So where is it curved? Come with me to a cliff by the sea.
Where space is curved
Imagine you’re standing on a headland overlooking a flat calm sea near an estuary. The water is saltier on the left than on the right. You see a single ocean wave, and notice that its path curves left a little because of the salinity gradient. The sea is an analogy for space. The salinity gradient is an analogy for a gravitational field. The ocean wave is an analogy for a photon. Now look at the surface of the sea where the wave is. It’s curved. It’s curved in a far more dramatic fashion than the curved path of the wave. This observation might sound radical, but see what Percy Hammond said in the 1999 Compumag: “We conclude that the field describes the curvature that characterizes the electromagnetic interaction”. See what Schrödinger said on page 18 of his 1926 paper quantization as a problem of proper values, part II: “classical mechanics fails for very small dimensions of the path and for very great curvature”. Also see what Maxwell said when he was talking about displacement current in 1861: “light consists of transverse undulations in the same medium that is the cause of electric and magnetic phenomena”. Where is space curved? Where the photon is. Because space waves.
Photon spin
Hence I would say a photon is a region of curved space. But I’d also say it’s like when you play classical guitar: you work the fret with your left hand changing the wavelength, but the amplitude of your pluck is always the same. When you do pluck, you make a wave, and the string is then curved. Try plucking a washing line whilst sighting your eye along it to watch the wave race away. Then try plucking in orthogonal directions with two different hands. I say this because we have linearly-polarized light, but we have circular-polarized light too, and the latter is thought to be more fundamental. I don’t know why. It’s as if in space there’s nothing to brace against. As if guitar strings are like infinite washing lines, and you have to pluck your guitar string with two plectrums at once, one vertical, one horizontal, with a linear separation between them. Then there’s a rotation of sorts, we have experimental proof of the spin of the photon. But the photon itself isn’t actually spinning. It has no magnetic dipole moment. The circular-polarized light wave is depicted as two orthogonal 90° out-of-phase electromagnetic waves propagating linearly through space with a combined left-or-right handedness, and so a spin of ħ or ‑ħ. The net electric vector is helical, but the circular-polarized photon isn’t going round and round:
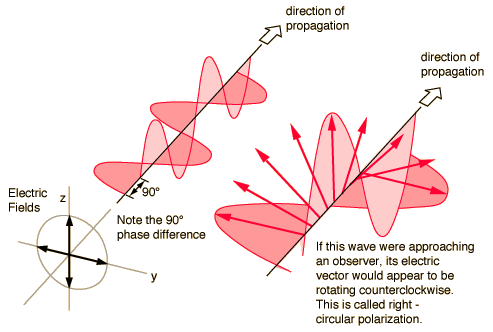 Image courtesy of Rod Nave’s hyperphysics
Image courtesy of Rod Nave’s hyperphysics
It’s like the circular-polarized photon is an arrow with one set of flights set behind the other. But this arrow isn’t spinning like a bullet. Your washing line isn’t spinning on its long axis like some drive shaft. For a better picture imagine you could lean out of an upstairs window with a whip in your hand. Move the handle quickly in a growing circle that then diminishes to make a wave that corkscrews down the whip, something like this:
I think the photon is something like this. Like you, it’s left handed or right handed, just like a screw thread. Because of the screw nature of electromagnetism, associated with the right hand rule. We’ll come on to that later.
What a photon is
But for now a picture is emerging. A picture that’s doubtless imperfect, but better than no picture at all. A picture of a photon that is a singleton soliton electromagnetic wave. A wave like half a length-wise lemon, with a twist. A corkscrew soliton in space, with a common amplitude that underlies Planck’s constant h. As to why we have this common amplitude, I’m afraid I don’t know. Perhaps I’ll have to settle for that’s the way space is. Perhaps animations of waves in a lattice will tell us something about it. And about solitons, and how they deform the lattice and alter the motion of solitons through the lattice. But for now, I think of the quantization of electromagnetic change written in 1994 by Robert Kemp. That’s the quantization of electromagnetic change, not charge. Kemp talks about saturation and maximum upper and lower potentials, and about the photon having a maximum electromagnetic amplitude in space, such that electromagnetic saturation is the cause of Planck’s constant. He also says this is what Vernon Brown predicted in his photon theory: “Brown predicted that the electromagnetic amplitude or saturation constant would be a constant from which Planck’s constant derives”. It’s as if space has an elastic nature described by permittivity and permeability, and an elastic limit, and so acts like its own waveguide. Because space is not nothing. It’s a polarizable medium, like some kind of ghostly gin-clear elastic. When an ocean wave moves through the sea, the sea waves. When a seismic wave moves through the ground, the ground waves. When an electromagnetic wave moves through space, space waves. And because of this, space is curved wherever that wave is. Not just in one dimension, but in two, because of the circular polarization. So space is curled, like your whip. Are Feynman’s wavy little arrows really corkscrews, showing this curvature? I don’t think so. But I do think that this says something about how pair production works. Because what does a 511keV photon do in gamma-gamma pair production? Or to put it another way: what does a hedgehog do when threatened?
 Hedgehog image ©
Hedgehog image ©
Cracking article John. I shall leave some constructive comments when I have more time. I like your insight that photons are not wave trains. You can turn that around and say that the wave trains idea arises from us observing collections of photons . The train is multiple photons end to end. Split any individual photon in a given train and a photon twice the length will leave, but also, the gap will be precisely filled by the increase to twice the length of the remaining photon. Split the photon by introducing a photon in antiphase to the original that cancels one half of the photons energy and you now have an experiment I would like to see.
Thanks Andy. But I don’t think that experiment is doable, because the photon is a soliton wave of 4-potential. In the middle of it E and B are zero, but the potential is at a maximum. The energy isn’t cancelled at all, it’s just not so obvious any more. But it isn’t totally hidden. Take a whole lot of photons and add a whole lot more in antiphase, and what you’ve got is a gravitational field. Look at the lattice cells up the centre of “>this picture and compare them with
“>this picture and compare them with  rel=”nofollow”>this. PS: try rotating the lattice cells and think spin 1 and spin 2.
rel=”nofollow”>this. PS: try rotating the lattice cells and think spin 1 and spin 2.
“Take a whole lot of photons and add a whole lot more in antiphase, and what you’ve got is a gravitational field.”
This is very intriguing – could you expand on what you mean by this statement?
See this depiction of a gravitational field?

 “>
“>

 “>
“>
.
.
Then remembering the canoe analogy, see this depiction of a photon?
.
.
Look up the middle. That’s where both E and B are zero. But there’s a still a field there. A gravitational field. Electromagnetism is where the cells are twisted. Gravity is where they’re flattened. A twisted square has a spin-1 symmetry. A flattened square has a spin-2 symmetry. The twisted squares are also flattened, but you don’t notice that so much. If you had a whole load of out-of-phase photons displaced to the left and right of the above by 1, 2, 3, 4, etc cells, the twist would disappear, but the flattening wouldn’t.
I shall have to look up the 4-potential soliton. Not something I have studied. However, just one point regarding you pointing out that all electromagnetic waves have the same potential magnitude. i.e. all photons have the same voltage magnitude. From a lecture at Manchester on my electrical engineering course I seem to remember the voltage of an EM wave being quoted as 3^.5/c or sqrt(3)/c. I have never found a reference to that anywhere else. I just wondered if you have. It is a number I have found useful.
It doesn’t ring a bell Andy. But it sounds like a golden nugget, because it chimes with the guitar analogy where the amplitude of your pluck is always the same. I’ll look into this. Many thanks. E=hf, E=Fs, and E=VQ for a reason.
.
PS: I googled on “voltage of a light wave” and found The Duality of Matter and Waves by Frank Znidarsic which led me to the Z theory of everything where I can see The elastic limit of space and the quantum condition. Unfortunately he says the gravitational force establishes the quantum condition.
I would like to point out that [u]photons never oscillate[/u]. This is a well known “novice” mistake. because of the nonsense taught in schools nowadays, any BS is “acceptable” in that place to discipline the kids… but we adults can know a lot better than that. Oscillation is what oscillators do, such as cavity oscillators or by way of spontaneous emission (atomic light) from which photons may be generated, one by one or many at a time.
A wave on the ocean “rolls”…. just think… the wave is the crest and the trough of a rolling progressive surface, it’s shape over time is always the same, you can follow this “form” away from the source, the longer the wave (spatially continuous) the more perfectly sinusoidal it is. This form “propagates” into the distance obeying the Inverse square law, plus an attenuation factor due to friction, sometimes the wind aids in regenerating the form, the “wave” retains this “form” until it finally breaks at an interface (the shore or a barrier).
The common surface wave in water is about the worst example of a propagating wave because of the awful frictional dissipation, there is a better example of a progressive “wave”… eg: the Modon. [url=https://en.wikipedia.org/wiki/Modon_(fluid_dynamics)]Modon (fluid dynamics) Wikipedia[/url], it is a special kind of soliton which is only known to exist in the Southern Ocean and can propagate virtually unaltered for [u]many months[/u] over distances of at least a couple of thousand kilometers, at a walking pace, and each end, which may be hundreds of kilometers apart, which is the “[u]granddaddy of a Falaco Soliton[/u]”, can propagate retaining it’s ability to move entrapped bubbles along it’s length to the remote end virtually in a neo-frictionless state beneath the ocean surface as a vortex. Exactly the same structures can be made using”photons”.
But while the propagation through space of this repeated form at the 2D surface of water is occurring, this “spatial harmonic” form is retained, the crests are like a moving boxcar on a train composed only of boxcars… the boxcars on a train “move past an observer” and appear to allow a light through it’s box and gap profile (with the backdrop of a setting sun or a street light shining from behind it, would seemingly show as “flashing motion”, but the “boxes” on the train are entirely stationary relative to the rest of the train and the other boxes and flashes are coming from different boxes at different spacing along the train. Nothing is moving on this “train of boxcars” excepting the wheels, and never will until it “breaks” at an “interface” (the train-stop) where there is a “crashing” of the line of boxes one against another). The boxes are the crests and the gaps between the cars (couplings) are the troughs. Yes… the train “moves” relative to a stationary observer using “wheels”. But as a “wave” this train is an analogy. In optics, repeating “wavelets” might be summed into continuous waves and visa versa… a train of wavelets can be broken up into a sequence of shorter wavelets.
Unlike an ocean wave which is an “irregular continuous phenomenon” like that produced by a continuously moving paddle, the individual photon is a single “impulse”. Think of a large lake on a still and breathless night. The surface is entirely flat. Then drop a single droplet of water into the surface at it’s exact center… there is a rapidly expanding circular wave, and it’s crests and troughs propagate away at the speed of waves in the surface of water while still all being confined to a narrow band in the direction of propagation. However this temporal disturbance as a band is confined to a “group” whose influence perpendicular to the circular wavefront is limited “spatially” to about twice the wavelength (that is twice the distance between the top of the crest and the bottom of the trough. On careful observation the leading and lagging limits of this impulse have a slightly higher frequency content of undulation than the central part… this is due to “truncation”. Once again the waves move but in water, which is a highly dissipative media, sometimes these higher frequencies may appear to be moving… like the leading turbulence at the front of a wave going up a tidal bore. You can even surf on that as it is subject to breaking. Unfortunately this wavelet system is undergoing a lot of frictional loss, and this generates that leading and lagging edge “temporal instability”. Before (leading) and after (lagging) this disturbance, the wave leaves the greater part of the ‘still” surface of the lake “more or less” undisturbed once more, even while the pulse is still propagating towards the edge of the lake. As in the first case this wave is expanding along the surface of a circle which is increasing and this decreases the amplitude of the wave as an inverse square law. That is a separate phenomenon to that of frictional dissipation since ISL spreading is only energy spreading not energy dissipation.
This overall outwardly propagating circular shape is a product of the way in which the droplet “strikes the surface” and in the way the source is “confined”. If the wave was “generated” using a special “pushing mechanism” in a box with an open end like an open ended bike pump, the strangely shaped wave will propagate in a closely defined mode in the direction of the “push”. This is a feature of the cavity and there can be oscillation in a cavity which is a much bigger subject… suffice to say the energy in cavities can be made to oscillate the fluid. There are some “side-lobes” generated” (wave spreading) but that is because it is not an ideally designed “pusher”. There are many “modes” by which a photon could be created. One special “pusher” for photons is the one-shot LASER. A wave passes down along tube of specially “doped” atoms whose energy states are “primed” in population inversion and can be triggered to be “fired” as a single wave and propagate along the length of the cavity. This waves “orchestrates” the push and the side-lobes are almost entirely perfectly attenuated. hence you have a pencil laser beam that begins and ends. A laser pulse.
Sorry Good Elf, your comment went into the spam folder, and I’ve been otherwise engaged. That’s interesting stuff about the modon. Did I say photons oscillate? I think of a photon as a single soliton pulse, where space acts as a wave guide. Maybe I need to tweak this article.
Wowsers! I just started reading the Physics Detective and am totally immersed into reading more. All of the math and much of the science is way over my head, but at least I have learned more about ” what makes things tick ” in several days than the previous 63 years of life ! Keep up the great writing Sir !
Many thanks Greg. I feel honoured. Comments like yours make it all worthwhile.
Is it possible that photon does not exist in physical world, it is just a math model for EM wave, heard from someone that we don’t have to invent photon, the pure wave can explain many things better.
I think the photon is the pure wave, Charles. Light exists, and it’s made up of electromagnetic waves. Each wave is a soliton, in that it doesn’t disperse. It’s a “light soliton”. I think of “photon” as a “light soliton”. Not a billiard-ball particle.
Thanks for replying, as you said, if photon is something like light soliton, will there be non-soliton light? Or EM wave always appear as solitons?
Light as we know it consists of photons, Charles, and as far as I know, photons are solitons.
.
Another type of electromagnetic wave is the evanescent wave, which is a standing wave.
What is the value of the Electromagnetic amplitude? If we do not know this, why?
Lu: as far as I know it’s 3.86 x 10ˉ¹³ m. Darn, I thought I’d said that. I say it in how pair priduction works.
Thanks for that. It is quite a flat wave. I try to visualize that and I see a streak of energy a wavelength long, too thin for me to see. I appreciate your write-ups, they are quite informative and understandable.
My pleasure Lu. But IMHO it isn’t so much a streak of energy as a wave in space. I think of it as something like a seismic wave, but in space rather than in the ground. I also think of it as an action rather than an actual thing. So I’m not sure that the word “thin” is apt here. I’m not sure whether it’s flat either. Maybe it’s twisted. Maybe we’ll have a better idea of that if somebody does some computer modelling, and says only a wave like THIS propagates as a soliton. The photon is where it all starts, but nobody can say with absolute clarity exactly what it is. Including me.
Thanks, John, definitely thought-provoking.
There is the thing that I don’t get though: If it is the space that waves, wouldn’t that mean that there is a preferenced inertial frame? In other words, how is that description of yours is in agree with the postulate that the speed of light is the same for all observers?
Yes, I think there is preferred inertial frame of sorts – the CMB reference frame. It isn’t an absolute reference frame in the strict sense, but it’s the reference frame of the universe, and the universe is as absolute as it gets. The measured speed of light is the same for all observers because of the wave nature of matter. See The Other Meaning of Special Relativity. by Robert Close. He uses a sonar analogy, and explains it really well. I referred to him in https://physicsdetective.com/the-nature-of-time/. He’s a good bloke is Robert.
I’m so very glad to see this query into the nature of light energy. I’m just beginning to read it, but already believe I have found a kindred spirit: https://ethicsblackhole.blogspot.com/2017/08/photon.html
Noted, David. I also note the final paragraph:
.
Einstein said: ‘All the fifty years of conscious brooding have brought me no closer to answer the question, “What are light quanta?” Of course today every rascal thinks he knows the answer, but he is deluding himself.’
According to my experimental evidence-based hypothesis, photon is made of two sub-quantum particles:
https://quantumantigravity.wordpress.com/hopfotrino/
Great article, except for your use of the term ‘soliton’, which refers to a non-linear wave phenomenon in normal usage.
Thanks John, and noted. I’ll have a look at that and see if I should fix it. Hmmn, I searched on “a wave that does not dissipate” and only one article turned up. It was a 1979 Sci-Am article called Solitons by Claudio Rebbi. It includes this in the abstract: A recent finding is that solitons may appear as massive elementary particles.
To me it made total sense, a soliton is a wave that keeps together as it travels, just like a photon does, just like the picture you have (fig 2 at the top) or a single wave in space, that’s a soliton. Sure, the sin and cos waves are ‘linear’ and solitons are non-linear, but lots of waves are non-linear. Example, in the ocean, you can approximate a long train of waves by sin and cos, but a single wave traveling along the ocean, with no other waves near it, can’t be, because sin and cos don’t stop ever, they stay as sin or cos all the way to the boundaries. So single waves traveling across the ocean are solitons which are non-linear which just means they have more complex formulas and you can’t do simple linear approximations to get sin and cos.
.
If you knew the soliton equations for a photon, perhaps you wouldn’t need quantum mechanics and you’d get a nobel prize. The linear waves (radio waves) are solutions for Maxwell’s equations which you get by assuming the electric field is cos(kx-wt) all the way to the boundaries. So a photon has to be a soliton, since it’s localized, and soliton solutions are non-linear, which is why it’s hard to figure it out.
Thanks Doug. I have a hunch we’ll find out via simulations of waves in a stiff cubic lattice. Or an actual demonstration of actual waves in a stiff cubic lattice. What do you have to do to make a wave that propagates linearly through that lattice? What does the lattice looks like as the wave is passing through? Does have to be something other than a cubic lattice? I have half a mind to try it out on my workbench, but I am just run off my feet these days.
Hi.
I think that your perspective on magnetism is interesting. I am not a science guy.
I found this on the internet:
Magnetism is a dielectric field, the loss of the energy or inertia manifests this three dimensional force vector in full extrapolation of which makes up the toroidal geometry of the magnetic field.
Magnetism is centrifugal force in motion.
Geometry of a hyperboloid towards counter space of increasing inertia and acceleration.
Maybe you can take a look at this: https://www.youtube.com/watch?v=nkIIdRJZybw
I would like to know your opinion on this.
Thank you.
I’ll have to get back to you Adam. It’s past bedtime, and I don’t want to wake the wife. A magnetic field is in essence a “rotor field”. That’s why people use the word “rot”. But I’m not sure it’s right to talk about a three dimensional force vector. If you put am electron in a magnetic field it will go round in circles, as will a positron. However the positron goes round the other way. The rotational force is the result of the electron or positron interacting with the magnetic field. Anyhow, I’ll take a look at the video.
“See the Wikipedia electromagnetic radiation article and note this: “the curl operator on one side of these equations results in first-order spatial derivatives of the wave solution, while the time-derivative on the other side of the equations, which gives the other field, is first order in time”. The orthogonal sinusoidal electric and magnetic waves in the depictions are somewhat misleading. The electric wave is the spatial derivative of the electromagnetic wave, whilst the magnetic wave is the time derivative”
I believe you’re misunderstanding what the equations are telling us. Maxwell’s equations have 2 wave solutions, one for each field, in the form of 2 differential equations. Their solution are functions that give the amplitude of the respective field. I’m not aware of any master wave equation that is also a solution and that has both E and B terms in it.
For the electric wave equation, we have
$$\nabla^2 \mathbf{E} = \mu_0 \varepsilon_0 \frac{\partial^2 \mathbf{E}}{\partial t^2}$$
(hope your site supports LaTeX)
The magnetic wave equation is analogous.
The corresponding solution is
$$\mathbf{E} = \mathbf{E}_0 f{\left( \hat{\mathbf{k}} \cdot \mathbf{x} – c_0 t \right)}$$
Applying the curl on this function is basically taking the spacial derivative, and as per maxwell’s equations this is also equal to the time derivative of the magnetic field. But we could have just as well taken the curl of the magnetic wave solution, ending up with an electric time derivative. E is NOT the tilt, it’s an amplitude! You get the tilt by applying the spacial derivative on E. B is NOT equal to rate of change of tilt, but rather the rate of change of B = tilt.
But we could have just as well said the same, switching places of B and E.
Sandra, you can do Latex by putting two dollar symbols before the expression, and two dollar symbols after. I’ve done it for you. See https://thimpress.com/add-latex-wordpress-website-learnpress-course-content/
.
In gravity we have a gravitational potential, and the gravitational field is the derivative of potential. The slope, as it were. In electromagnetism, we also have a potential A, and the electric field is the derivative of potential. The slope as it were. It’s A that relates to the amplitude. We also have magnetism, the real field is the electromagnetic field, so things are more complicated. But not so complicated that we can’t understand them. You might like to take a look at https://physicsdetective.com/the-screw-nature-of-electromagnetism/ where I talk about twist and turn. Or https://physicsdetective.com/the-theory-of-everything/ where I talk about spin 1 and spin 2 and relate electromagnetism to gravity.
I have no issue with the electric field being the derivative of the electric potential. It’s just that the quote you’re taking from Wikipedia does not talk about that. The derivatives are of the electric and magnetic fields, not their potential.
I believe talking about the derivative of the 4-potential would be more correct for your argument.
Sandra: the problem with what you’re saying is that the derivative of a sine is a cosine, which would mean E and B are out of phase, and they aren’t. Hence the relevance of the space and time derivatives of electromagnetic 4-potential. As for whether I’ve misquoted Wikipedia, the page has changed an awful lot. It’s as if some Wikipedia war has been waging. I’m not sure the authors appreciate the “screw nature of electromagnetism”, which both Maxwell and Minkowski talked about: “a motion of translation along an axis cannot produce a rotation about that axis unless it meets with some special mechanism, like that of a screw”. Like I said, it’s all about twist and turn. Twist is the spatial derivative of potential, turn is the time derivative. There is more than one way to skin Schrödinger’s cat.
Sandra: I’ve changed the post to alter this:
.
The electric wave is the spatial derivative of the electromagnetic wave, whilst the magnetic wave is the time derivative.
.
to this:
.
The electric wave is the spatial derivative of a wave of electromagnetic potential, whilst the magnetic wave is the time derivative.
Hi again Sandra: ” I’m not aware of any master wave equation that is also a solution and that has both E and B terms in it.”
.
Exactly, we need to find the master wave equation, then perhaps a proper description of photons and electrons, etc can be found. The E/B photon description doesn’t provide QM anyway, so we know it’s just an approximation for large amounts of photons (i.e. radiowaves). I don’t think we will find analytical solutions but rather it will be ‘discovered’ by running 3d simulations.
.
The way to do it would be to reduce E and B to a single field (I will call it E). The restoring force for the wave is quite confusing, you hit space soft, you get a long wavelength (e.g. radiowave), and the restoring force is very low because it takes a long time (low freq). You hit space really hard, you get gamma rays, now the restoring force is much higher, since the freq. is higher. Either way there’s a constant of ‘h’, which in some sense is the constant amplitude (i.e. photoelectric effect) talked about here. It must be related to the fact that the restoring force acts like a non-newtonian fluid, weak for long waves, very hard for short waves.
Doug: I see it as something like a guitar string. Put your left hand on the fret, press hard, and pluck. Now move your left hand half way down the neck of the guitar. Press hard and pluck again. Make sure the amplitude of the pluck is the same.
.
Only people say photons have a circular polarization, which means they aren’t straight up and down transverse waves. Hence my penultimate picture above.
Very interesting analogy, thanks for making it clearer!
.
After reading your stuff on Maxwell’s equations, in that B doesn’t create a curl in E, since the “=” sign isn’t a “create” sign, it’s equal. Or a circular current doesn’t create a magnetic field, it is literally equal…. so now I’ve started to try to just think about everything in terms of E. Idk if it’s possible.
My pleasure Doug. I think that canoe analogy is important. The photon is an electromagnetic wave, and an electromagnetic wave is not comprised of an electric wave and an orthogonal magnetic wave. The electromagnetic wave is the simplest example of electromagnetism. Things start to get more complicated when you start dealing with waves in a closed path and charged particles.
According the Big Bang model of the universe, the expansion of space stretches the wavelength of a traveling photon over time, causing its redshift. For example, an observed CMB photon freed during the recombination era has its wavelength stretched 1090 times to change from infrared to microwave. I am interested in your thoughts on this idea and whether ‘the photon must be some kind of a singleton soliton light’ changes anything.
Jim, apologies, your comment was in the spam folder for some reason.
.
I think the CMB photon is like the ascending photon, the wavelength doesn’t increase. See the last section of https://physicsdetective.com/the-big-bang/ where I refer to the Tamara Davis SciAm article Is the Universe leaking energy? (https://kaiserscience.files.wordpress.com/2015/08/is-the-universe-leaking-energy-law-conservation.pdf). The answer would seem to be no.
I like to come back once in a while to reread the articles, and everytime I find something new to question.
You say that h (units of momentum x distance) indicates that all photons have the same amplitude (please correct me if this is not what you meant). So let’s take two laser beams, each at a different frequency v1 and v2, but both composed of the same number of photons per unit time. We know that I (intensity) is proportional to the square of the amplitude, so A ~ √I.
Since E = hv, the intensity is proportional to the number of photons (multiplied by velocity of propagation of the energy, c): I ~ n*E*c = n*h*v*c.
Joining the relations above, we get A~√n*h*v*c. If n is the same for both beams, it follows that at different v1 and v2 they have a different amplitude. How can this be if all photons share the same amplitude?
On a side note, I still think you misunderstood my comment on the derivatives. You’re ascribing, in the blogpost, the tilt to the derivatives of the fields, not the potentials, because in Maxwell equations the terms E and B refer to the fields, not the potentials. But then in your last answer you talk about the tilt being the derivative of the potential, which is correct, but then it has nothing to do with Maxwell equations. You’re mixing things up I’m afraid.
Sandra, I have to dash, but in brief: yes, I meant to say that h (units of momentum x distance) indicates that all photons have the same amplitude. I also meant to say that this amplitude is a real physical distance. As for the laser, increasing the laser amplitude is associated with cramming more photons into the beam, not with changing the photon amplitude. I’ll check what I’ve said in the article and comments, but my intent was to say there is only one potential, and the E field is the spatial derivative of it, whilst the B field is the time derivative of it. I don’t know if you’ve read https://physicsdetective.com/the-theory-of-everything/ yet, but perhaps it might help. I’ll get back to you properly when I can.
Don’t worry about how fast you can answer, it’s your blog, your time.
Read better what I wrote please. If we cram the same number of photons in the two beams (same n), the resultant amplitude depends only on the frequency of the photons, i.e. if photons have all the same base amplitude the total amplitude of the beam is NOT the sum of that of all photons, rather it’s different for each beam at different frequency. It’s very simple math, I just put together the relations a) I = E*c,
b) I ~ A^2 and c) E= hv.
It might be simple math Sandra, but it’s apples and pears. Yes, beam intensity I = Ec ~ A² where A is amplitude. But this amplitude is not the same thing as photon amplitude. I’m saying the latter is an actual wave amplitude for a singleton soliton electromagnetic wave. A distance implicit within the momentum x distance of action h within the statement energy E = hf = hc/λ. It’s like you pluck a guitar, and the amplitude of your pluck is always the same regardless of the wavelength, which is determined by the position of your other hand on the frets.
.
The beam amplitude is something else. See for example this article. It says “the amplitude is the maximum field strength of the electric and magnetic fields”. Note that I said electric field E is the spatial derivative of potential. That means electric field E, and hence beam amplitude, is associated with the slope of the photon wave. Not the height. This means you can increase your beam intensity and “amplitude” by crowding your photons together, but you aren’t changing the photon amplitude.
Firstly ,thank you for your exciting blog. I couldn’t stop reading and missed half a nights sleep.
I don’t quite understand your criticism of the wave packet. If the photon had an exact energy E without any uncertainty dE, wouldn’t that imply, from simple fourier analysis, that the wave train would be temporally infinite?
Thanks Avishai. As far as I know the photon has energy E=hc/λ, and conservation of energy says the energy doesn’t vary. Hence the wavelength λ doesn’t vary either. That wavelength is the wavelength of the photon, which seems to me to be a single “soliton” wave rather than a wave train. Whilst we often see wave trains in nature, such as in the ocean, we don’t think of a succession of ocean waves as one wave. I think of the photon in a similar fashion. But having said all that, I’m still not 100% sure of the exact nature of the photon. I would like to see computer modelling in some kind of lattice, which might tell us something. However I haven’t had the time to do it.
It is hilarious that some folks at the PhysicsForums actually think this image shows that the electric fields and magnetic fields are perpendicular to each other by saying “Those fields are perpendicular. You can see that from the 1:4 relationship between the offset and pitch of the helices.” I don’t understand the comment at all.
shows that the electric fields and magnetic fields are perpendicular to each other by saying “Those fields are perpendicular. You can see that from the 1:4 relationship between the offset and pitch of the helices.” I don’t understand the comment at all.
Another article also said the circular polarized EM field to be orthogonal which I find strange, the following excerpts from the article are “Fig. 3.1 shows three cases of plane waves defined by the following electric fields: Figure 3.1. Plane waves with 1) linear, 2) circular, and 3) elliptic polarizations where 1) corresponds to linear polarization, 2) to circular polarization and 3) to elliptic polarization. It is clearly seen that the E and the H fields are orthogonal and equal in strength at each time instance”. and this is the picture of the circular polarized EM field . The only EM field that is perpendicular there is the typical linear polarized EM field, unless if we interpret the elliptic polarized EM field as something that is also orthogonal.
. The only EM field that is perpendicular there is the typical linear polarized EM field, unless if we interpret the elliptic polarized EM field as something that is also orthogonal.
I still find it very confusing on why they are insisting the circular polarized EM field as something that is orthogonal.
Mohamed: that sort of thing annoys me. It’s the electromagnetic field. Sometimes I feel as if Maxwell’s unification never happened. Physics Forums should not be teaching such lies to children.
Any thoughts about that, John Duffield? “Those fields are perpendicular. You can see that from the 1:4 relationship between the offset and pitch of the helices”, what does that mean? Sorry, English isn’t my native language.
Like I said that sort of thing annoys me. It’s the electromagnetic field. It’s an electromagnetic wave. Not an electric waves and a perpendicular magnetic wave. Physics Forums should not be teaching lies to children, but sadly it’s more interested in being mainstream than being honest.
‘When you chop a photon in half with a beam splitter to convert it into two photons, each has twice the wavelength as the original’
I’m a bit confused by this statement.
Dave: It’s just E=hc/λ and conservation of energy. If you convert one photon with energy E into two photons, each photon has an energy that is half that of the original photon. In similar vein each photon has a wavelength that is twice that of the original.
I think you could add this idea to the picture.
Normal, plane waves exhibit damping after going through a slit and start spreading in all directions, because of the r^2 rule.
.
But photons, even of we consider them single waves, don’t. When they hit an obstacle, the full energy of the original photon before the slit is transferred to the obstacle, it doesn’t damp down with distance. And yet, we still notice a probability distribution that resembles that of a damped wave, only we need many many photons to notice this. How can we explain this phenomenon?
.
We’re not taking into account a very fundamental property that photons have. Spin.
.
Photons are a direct result of the interaction between matter and the EM field; they represent an energy exchange. When the electron bound to an atom transitions between different modes of vibration, how does that transition occur? Standard QM teaches that it happens instantaneously, but obviously that is just sweeping it under the carpet. In vibrations on a string the transition happens by emission (or absorption) of a BEAT FREQUENCY. But electrons, contrary to elastic strings, also have orbital angular momentum (the wave itself is rotating), so by virtue of angular momentum conservation when the transition happens the beat frequency must also carry away this angular momentum. Guess what is the momentum difference between adjacent energy levels on the hydrogen atom? hbar.
.
The fact that photons are SPINNING is what’s preventing them from damping out, and keeps them localized! Think of the liquid in a cup of tea, and spin it vigorously. You’ll notice how the faster it’s spinning, the more squashed up towards the center the vortex will be. The photon gets “squashed up” in a similar way, and a photon is spinning extremely fast! For this reason, I believe it is incorrect to assume all photons have a common amplitude. What they have in common is the same angular momentum. By saying “rolling your marker fast or slow, but along the same circumference” we are not conserving angular momentum. We should think about it as “roll your marker around different circumferences, all at different speeds”. Just like ice-skaters, they go faster when they pull their arms in. Because of angular momentum conservation. And hbar relates to angular momentum, not amplitude.
.
I can show you why this must be the case:
angular momentum is L= h/2π = MVR, where R is the radius of the orbit. A photon moves at C, so v=c. For the mass we just take the Einstein relation E=mc^2, and for energy we use E=hc/lambda. With a bit of algebra, we get to R/lambda = 1/2π. You can clearly see that the radius (=amplitude) of the photon decreases if the wavelength increases.
.
.
How do we relate all this to the slit experiment? When the photon goes through the slit it needs to conserve angular momentum, but that angular momentum is quantized: this means it can’t spread out, otherwise each part of the wave would have a smaller amount of angular momentum. The result is the wavepacket is deflected in a particular direction according to local interactions that depend on the phase of the wavepacket.
.
To understand this, imagine the photon as a point moving on a circle. The point represents the phase of the photon. When the photon goes through the slit it will have a certain phase. If the slit is visualized as 2 walls, and the photon is rigid, the plane of the circle representing the photon will tilt according to which wall the point is touching. I might add a comment below with links to images, to show this better.
Here’s the image: https://imgur.com/TznsTfb
The nature of the “interaction” is the same as that of refraction: the walls slow down the photon on one side, causing it to curve. Since the amount of interaction depends on the overlap between the phase and the wall, the following photon distribution on a following detector will look like a normal distribution.
I’m still thinking about how to understand the double slit experiment under this view.
I must correct some typos here.
.
“We should think about it as “roll your marker around different circumferences, all at different speeds””
.
I actually meant “We should think about it as “roll your marker around different circumferences, all at the same tangential speed, and different angular speed”
.
.
“You can clearly see that the radius (=amplitude) of the photon decreases if the wavelength increases.”
.
I meant to say “radius of the photon increases if the wavelength increases”
Leon, I’m sorry I haven’t replied sooner. You are in italics:
.
Photons are a direct result of the interaction between matter and the EM field; they represent an energy exchange.
.
They do, but I would add that IMHO matter is just a knot in the EM field. The electron is a trivial knot, the proton is a trefoil knot, the positron and the antiproton have the opposite chiralities, and there are no other stable matter particles.
.
When the electron bound to an atom transitions between different modes of vibration, how does that transition occur? Standard QM teaches that it happens instantaneously, but obviously that is just sweeping it under the carpet. In vibrations on a string the transition happens by emission (or absorption) of a BEAT FREQUENCY….
.
Yes, I thought that video with the strings and loudspeaker coils was great stuff.
.
The fact that photons are SPINNING is what’s preventing them from damping out, and keeps them localized! Think of the liquid in a cup of tea, and spin it vigorously. You’ll notice how the faster it’s spinning, the more squashed up towards the center the vortex will be. The photon gets “squashed up” in a similar way, and a photon is spinning extremely fast! For this reason, I believe it is incorrect to assume all photons have a common amplitude. What they have in common is the same angular momentum. By saying “rolling your marker fast or slow, but along the same circumference” we are not conserving angular momentum. We should think about it as “roll your marker around different circumferences, all at different speeds”. Just like ice-skaters, they go faster when they pull their arms in. Because of angular momentum conservation. And hbar relates to angular momentum, not amplitude.
.
Interesting stuff Leon, but note that Plank’s constant h is a constant of action, and the dimensionality of action can be expressed as either momentum x distance or energy x time. In addition we typically write photon energy as E=hc/λ. The c is a conversion factor between distance and time, such that photon momentum p=h/λ. Then photon momentum is inversely proportional to wavelength. Since ћ=h/2π, I’m not seeing the same angular momentum for all photons.
.
I can show you why this must be the case: angular momentum is L= h/2π = MVR, where R is the radius of the orbit. A photon moves at C, so v=c. For the mass we just take the Einstein relation E=mc^2, and for energy we use E=hc/lambda. With a bit of algebra, we get to R/lambda = 1/2π. You can clearly see that the radius (=amplitude) of the photon decreases if the wavelength increases.
.
There’s a couple of issues here, in that all photons moves linearly at c, and photons don’t have mass, so using L=MVR and E=mc² is a problem. For example, you said “roll your marker around different circumferences, all at different speeds” but then you used a speed of c. Not only that, but the ice skater analogy is backwards. Don’t get me wrong, I do think photons have a spin, but I’d like to see experimental proof rather than a mathematical proof.
.
How do we relate all this to the slit experiment? When the photon goes through the slit it needs to conserve angular momentum, but that angular momentum is quantized: this means it can’t spread out, otherwise each part of the wave would have a smaller amount of angular momentum. The result is the wavepacket is deflected in a particular direction according to local interactions that depend on the phase of the wavepacket.
.
The problem with that is that you can split a photon into two. That’s what the later quantum entanglement experiments do via spontaneous parametric down-conversion
.
To understand this, imagine the photon as a point moving on a circle. The point represents the phase of the photon. When the photon goes through the slit it will have a certain phase. If the slit is visualized as 2 walls, and the photon is rigid, the plane of the circle representing the photon will tilt according to which wall the point is touching. I might add a comment below with links to images, to show this better. Here’s the image: https://imgur.com/TznsTfb. The nature of the “interaction” is the same as that of refraction: the walls slow down the photon on one side, causing it to curve. Since the amount of interaction depends on the overlap between the phase and the wall, the following photon distribution on a following detector will look like a normal distribution. I’m still thinking about how to understand the double slit experiment under this view.
.
I think you’re on the right track with that. Can I just say that I don’t like the use of points. The photon has a phase because it has a wave nature. That’s why it gets refracted. Moving on to your further comments:
.
I actually meant “We should think about it as “roll your marker around different circumferences, all at the same tangential speed, and different angular speed”
.
Good one.
.
I meant to say “radius of the photon increases if the wavelength increases”.
.
Another good one. That makes me think of the bullwhip. When you lean out of the upstairs window and rotate the handle fast you have a tight spiral wave moving down the bullwhip. When you rotate it slow you have a looser spiral wave moving down the bullwhip, and you could rotate it round a wider circle. But a wave in space isn’t the same as a bullwhip, a better analogy would be to grab a part of a stiff lattice and move it like the handle of the bullwhip. The disturbance that then propagates through the lattice has a rotation to it, but it doesn’t have a radius as such. In similar vein a seismic wave might move your fridge back and forth by 1 metre, but the seismic wave is not a metre wide.
.
An animation or simulation might help with this sort of thing. Maybe the guy who did the beat frequency experiment could help with that. Darn, I can’t find it.
Leon, I love the skater analogy, also tea cup vortices. One important aspect of John’s writings that I was made aware of and often gets overlooked is the actual mechanical/physical aspect of EM, with energy and the tranfer of said movements. That chirallity,spin,vortices,dipoles,ect….are all three dimensional, physically performing mechanical-like work states ?
Also: would your tea cup scenario work for why black holes have jets ? I agree with John about : 1. The frozen star theory 2. That too much matter & quantum particles are getting sucked in too quickly and can’t be decompressed/cooled-down/correlated all at once and therfore sone has to go back out, all in a very old-fashioned mechanical manner.
It’s really hard to think in 3D. Generally, it’s easier to think about models in 2D and then expand that to 3D. But doing so comes with the cost of not being able to model more complex behaviour, like rotational motion coupled to a linear motion.
In this image https://imgur.com/a/MZJXO1s I’ve made a thorough description of the math involved. It’s really easy stuff. I wonder if there is anything wrong with this, it looks too easy for noone to have thought about it before.
Relativistic jets do look like that for a similar reason. Close to the event horizon the angular momentum becomes so big that all matter and radiation is funneled along the axis of rotation, and then gets ejected due to the immense pressure building up. But obviously that’s not the whole story: black holes are extremely complex bodies, and this is probably not the only cause of the jets. From wikipedia:
.
“Because of the enormous amount of energy needed to launch a relativistic jet, some jets are possibly powered by spinning black holes. However, the frequency of high-energy astrophysical sources with jets suggest combinations of different mechanisms indirectly identified with the energy within the associated accretion disk and X-ray emissions from the generating source. Two early theories have been used to explain how energy can be transferred from a black hole into an astrophysical jet:
.
Blandford–Znajek process. This theory explains the extraction of energy from magnetic fields around an accretion disk, which are dragged and twisted by the spin of the black hole. Relativistic material is then feasibly launched by the tightening of the field lines.
.
Penrose mechanism. Here energy is extracted from a rotating black hole by frame dragging, which was later theoretically proven by Reva Kay Williams to be able to extract relativistic particle energy and momentum, and subsequently shown to be a possible mechanism for jet formation. This effect includes using general relativistic gravitomagnetism.”
All graphics are greatly appreciated by my old, slow ass. As a scientific layman, even I could immediately recognize one of the top illustrations as the gamma ray high end of the EM spectrum. The long radio waves of the bottom graphic.
Pingback: Left Vs Right – Reject 5G
FUN FACT : We humans are scientifically defined by CHIRALITY as well when it refers to us being right or left handed.
As a natural southpaw I fully admit to being throughly evil and completely destructive ; therefore worthy of banishment from the Physics Detective if found necessary.
I also am going to start my own blog furthering the most neglected story of long suffering 👈 leftys the world over ! And combine this cause along with the dire need to stop 6 & 7 G from MASERing Humanity into smithereens…………..or an even more paranoid state of minds !
“As a natural southpaw I fully admit to being throughly evil and completely destructive ; therefore worthy of banishment from the Physics Detective if found necessary.”
.
I am, of course, left-handed.
Of course! Now it all make sense !
Poor John’s Almanac will survive to infinity and beyond……
http://exvacuo.free.fr/div/Sciences/Dossiers/QM/Juliana%20Brooks%20Mortenson/Juliana%20Brooks%20Mortenson%20-%20Hidden%20Variables,%20The%20Elementary%20Quantum%20of%20Light.pdf
Hidden variables in Plancks constant – see also a reanalyses of Planks constant by Lori Gardi using dimensional analysis.
Eric Reiter comes to the same conclusions based on his beam splitting of gamma rays.
Thanks for that Andrew. That looks like good detective work by Juliana Brooks:
.
”Although the photon has long been held to be the elementary quantum of light, that understanding must be re- examined. It appears to have arisen from limitations in Planck’s abbreviated quantum formula. The hidden time variable in Planck’s condensed quantum formula was fixed at a value of one second. The photon was subsequently interpreted as a packet of light, with its energy defined by Planck’s quantum formula, E = hv. Use of this condensed quantum formula to calculate photon energies, inadvertently defined the photon as an increment of light of one second’s duration. The photon energies to which we are all accustomed, are thus the amount of energy in a one second measurement of light, regardless of the light’s frequency or wavelength. The unsatisfying result of this definition was a fundamental particle of light whose energy was infinitely variable. Dissatisfaction with prior interpretations of the “photon” as an indivisible and elementary quantum of light appear to have been well-founded. An arbitrary, one second measurement of energy cannot be a truly indivisible and elementary particle of nature…. Accordingly, the single electromagnetic wave or oscillation is the true elementary particle of light”.
.
I will look into this further. Tsk, it dates from 2009, and there’s only 7 citations: https://www.semanticscholar.org/paper/Hidden-variables%3A-the-elementary-quantum-of-light-Brooks/c61c64e28018a8adde005701c8b5868152ce0c80
.
I’ll look at what Lori Gardi says too: https://www.researchgate.net/publication/325462944_Planck%27s_Constant_and_the_Nature_of_Light
I imagined being a photon and here are some of my thoughts. I am solo
I am legion. I am Alpha and Omega I’m complex in the beginning I spiral out never ending
I come and go from the electron who is me in a confined collection
You can’t see me as I travel, only when I have arrived
Make haste and never catch me
If we resonate you will accept me, if not you redirect me.
If you can see me we I will not hurt you
If not I may desert you
This is only a small part of me
You will never completely see me
“the amplitude of all light waves is the same regardless of frequency”
You introduce this but never justify it. So what were you getting at, John.
Dave: I was saying photons are transverse waves in space, where space literally waves. I was also saying Planck’s constant of action h is common to all photons, and the dimensionality of action can be expressed as momentum x distance. So my claim is that the amplitude of the transverse wave in space is the same for all photons, regardless of wavelength, like we see in the depictions of the electromagnetic spectrum.
The photon does have a spin, such that the transverse wave is twisted. Hence ”roll your marker round fast or slow, but roll it round the same circumference, because Planck’s constant of action h is common to all photons regardless of wavelength”.
Everytime I read such articles written by PD, it is like first birth again – all those decades of guessing about charm, quarks, quantum computers, all that nonsense crashed by John and like. Looking forward, amazed.
Thank you Tony. The more I’ve learned, the more I’ve thought that fundamental physics is simpler than people think. I think it all comes back to William Kingdon Clifford’s space theory of matter: https://en.wikisource.org/wiki/On_the_Space-Theory_of_Matter. A photon is a wave in space. A 511keV photon can get stuck in its own curvature, whereupon we call it an electron. And so on.
T hanks.
Surely, the half wave shown in Figure 3 would carry a charge. The wave would have to encompass a complete cycle to remain neutral.
No. Charge is what you get when you wrap up the wave, which is a field variation, into a twisted double loop. The result appears to be a standing field, but it isn’t really motionless. Take the spatial and time derivatives of the “half wave” to yield the E and B waves that are usually depicted:
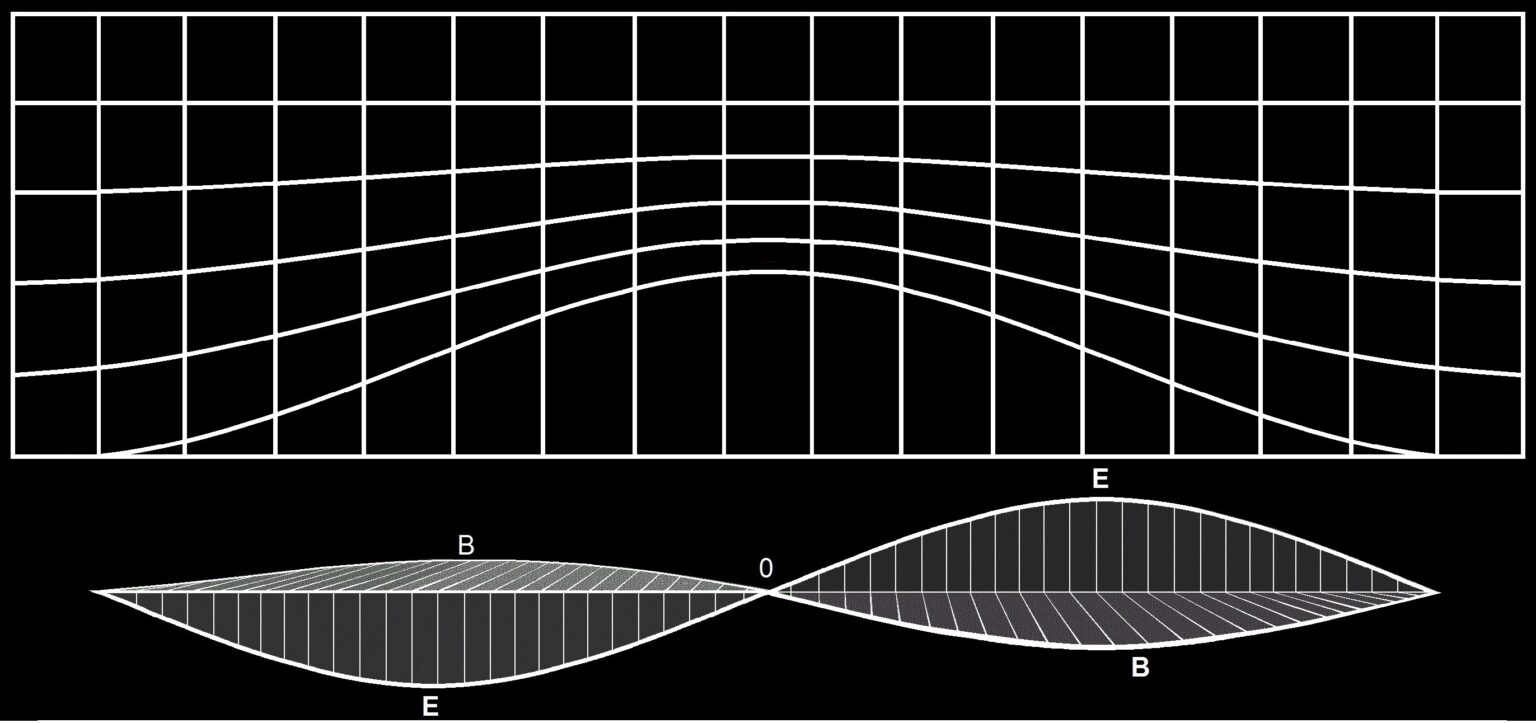
See https://physicsdetective.com/guidance-notes-for-simulations/ for more on the subject.
Sir Detective,
I linked to this article because a lot of researchers need to “get up to speed” (so to speak) on photons (The Photon Current – 22).
My spam meter is on the move, Dredd. Please keep your comments relevant to the article.
Sir Detective,
Ok. Quantum oceanography is going to new photon concepts. For example photon transitioning [“empty hybrid mode from a ‘virtual-free’ photon mode”] (Journal of Physics Communications)..
Note that the bottom of the oceans on Earth are less mapped than the surface of the moon or Mars (negligence).
I am just pointing out that the photon is becoming more of a factor in some of the science disciplines that haven’t focused on it enough.
Your assistance leading to a better understanding for those laboring in those disciplines would prove fruitful IMO.
“…exit spectral intensities at equilibrium temperature T carry quantum information on the energy density of matter excitations coupled to photons…”
Sorry Dredd, but this is climate change pseudoscience. Look, I’m all for free speech in science, but any more comments like this, on this article about the nature of the photon, and I will delete your comments. Quantum information my arse.
I completely agree that these articles have changed my entire concept of energy and matter. I now find my self laughing out loud about the complete ridiculousness of almost anything related to quantum mechanics. I was never ever a believer in entanglement, but since almost every source said it was the truth and “proven” it has taken me so long to finally see through the complete BS.
Quantum physicists are still grasping with the age old joke “If a tree falls in a forest and nobody hears it does it make a sound?” With the whole conscious observer, and how a measurement supposedly collapses the wave function, and does it need to be conscious, and quark colors, and gravitons and parallel universes! What the hell is all that crap?!
Look I think things got totally derailed when trying to determine the location of an electron, it was just moving too fast for us to measure and so we knew the shape of the cloud that it was in, but we couldn’t measure where it was exactly so then it was just assumed it MIGHT be anywhere, and then a whole probabilistic theory and quantum model was build around that. QM models probabilities, but it is not actual. 1) The electron is only in 1 place at 1 time, so there is NO Quantum superposition. 2) There is also no entanglement, no spooky or instantaneous action at a distance, and no collapse of the wave function at the opposite end of the universe when a “measurement” is made. Since these two central premises are not true, the rest of quantum mechanisms just falls apart.
I love physics, studied hard core physics, and have always love physics but have been completely turned off by quantum mechanics for over 25 years. This site has re-energized me and brought the love back and I have been thinking about things that I haven’t thought about is so long. It also makes so much sense! Thank you John.
A thousand thanks Andy, I really appreciate it. Comments like yours make it all worthwhile. Keep on rockin’!
Andy: “since these two premises are not true the rest just falls apart”
.
Since eggs clearly are not laid two at a time chickens can’t be real. That’s what you are saying. How can you so confidently have such an opinionated belief without even understand what an operator is? Because I bet you don’t, since the detective never talks about it. He never talks about the actual content of the theory, only of his vision of them through popular science books and articles. That’s why he never delves into the actual math, and never replies to math arguments.
.
For the last time, I suggest you take your information from other sources as well.
Oh Sandra… you laid out such a great argument here. “Since eggs clearly are not laid two at a time chickens can’t be real.” Lets analyze that shall we? How about we use one of your favorite models – quantum mechanics, a model that you yourself apparently don’t fully ascribe to, since you said you don’t believe in one of its central tenants (Entanglement), but that you seem to continue to be defending despite your disbelief (kind of like you have some physics stockholm syndrome?)
– So a chicken lays an egg, the egg lands in a nest, and everything is good right? Well, welcome to quantum mechanics, where your assumptions go to die. Lets ‘lay’ out the model: The Chicken is the Quantum system. The number of eggs or ‘egg states’ is the observable quantity (discrete eigenvalues). Laying an egg is a Quantum transition, and you counting the eggs is the actual measurement (collapse of the wavefunction).
– So according to your position operator, an egg doesn’t just get laid somewhere, it exists in a smeared-out wave across all possible nesting locations. In fact, there’s a perfectly legitimate chance according to quantum mechanics that the egg could end up on the roof of the barn, or phased halfway into a fence post, because, in quantum terms, the egg isn’t anywhere until you look! You know speaking of your operators Sandra, I love how even something as simple as a momentum in quantum mechanics requires the use of imaginary numbers to make the math work out.
– But we’re just getting started. Meet the number operator N, which in theory tells us how many eggs have been laid. Seems simple, right? Until quantum mechanics rolls up and predicts that the chicken might have laid 1 egg, or 100, or a negative one. Yes, quantum physics allows for the mathematical possibility of an unlaid egg, an egg that exists only as a subtraction from the platonic ideal of eggness. Before you open the coop, the chicken is in a superposition of all possible egg counts. That is literally what quantum mechanics is predicting.
Now meet your complex Hamiltonian operator, the god-operator of energy that decides how this cosmic egg show unfolds in time. It governs everything from the chicken’s velocity to the potential barriers in the coop, including that solid wooden wall between the chicken and the nest. What great things does the Hamiltonian operator predict: Well it predicts that your chicken might just quantum tunnel straight through the wall and lay her egg on the other side like it was nothing. Even better: through quantum teleportation, the chicken’s egg-laying state could be transmitted instantly across space, meaning the egg could “appear” in another coop hundreds of miles away. Except don’t worry, that doesn’t break all the known laws of physics since it’s not really the egg, it’s just the ‘quantum information’ of the egg-laying event, reconstructed from entangled feathers and statistical despair. Ahh, all makes sense right? But don’t worry sleep well, the top physics people have sorted this all out for you. Don’t think too deeply about it, just trust them, because they have some blips on a chart that proves it all! If someone does find an inconsistency, then boop! a new particle is created to come to the rescue!
– Anyway, Sandra I have no clue why you responded to my post and insulted me. I do get my information from multiple sources, so lay the F off. While knot theory in math goes back a long way it was not really until the 80’s and 90’s when people really starting working it. Similarly a soliton wave is quite complex to model mathematically over a continuum, and obviously cannot be modeled by your simple sin and cos functions which you love to quote and get yourself all in a ruffle about.
.. and by unlaid egg, I mean an egg that is laid and is then unlaid as in it goes back inside the chicken after it is laid, this is the magic of quantum transitions! A particle is here then it is there, then it is nowhere, then it is everywhere at once! Again like a cheap magic trick.. this superposition is the central principle of quantum mechanics. Insane purely probabilistic theory taken to ridiculous extremes by mathematical constructions which are then claimed to be ‘proven’ by dubious science, believers wanting and needing to believe, and whack logic arguments. So tired of talking about all this quantum BS. It is a cult.
Andy: you clearly have no idea what you are talking about. You probably looked up on chatGPT the name of some operators without understanding what they actually represent. An Hamiltonian operator is simply the energy of a system, kinetic + potential, it’s purely a classical concept. It has nothing to do with tunneling. The imaginary units in QM are there to represent a phase, you know, like in the Euler identity e^itheta = costheta + isin(theta)? Which traces a circle? Or in the Pauli matrices, where it has the function of a volume element?
.
“and obviously cannot be modeled by your simple sin and cos functions which you love to quote” so you’re agreeing that Malus law does not work. Good. That’s all I wanted to get in your head.
.
You seem to despise statistical theories in general. Well, thermodynamics is a statistical theory. Guess that also is pure bullshit. Nevermind!
.
You think I’m contradicting myself when I say spooky action is wrong, despite me clearly saying how that is not the case. That is all one needs to understand that you truly have no idea what you are talking about. That would not be a big deal of you actually had the self awareness to understand when you don’t understand something. You know what? Stay in your fantasyland where all scientists in the world are out to lie to you for personal gain. Must be a very nice place.
Andy: I’m sorry, I believe in free speech in science, but sometimes there are… issues with that.
I do so wish that people would refrain from insult and abuse. But they don’t. Especially when they have some kind of conviction in something. Such as higher dimensions. Or instantaneous spooky action at a distance. For which there is no evidential support. People just want to believe, Andy. In heaven and hell and sweet baby Jesus. In 72 virgins in paradise. In time travel, in the path to the parallel antiverse, and so on. I recommend that you have a read of the psychology of belief.
You too Sandra. Sorry again.
No need to be sorry Boss.
If I can refrain from all Ad Homien attacks, then all other much younger adults should be able too. I constanly need to remind myself to be an ethos/logos based student first, a pathos based expert dead last……….
Sandra, I don’t claim to be an expert in Quantum mechanics, but unfortunately it is quite sad that you are very wrong again and don’t appear to understand some of the basics. No ChatGPT was used in my response. A quick google search should have led you to articles explaining the Hamiltonian in more detail if you chose to read them and not an AI summary.
.
You stated in your response: “An Hamiltonian operator is simply the energy of a system, kinetic + potential, it’s purely a classical concept. It has nothing to do with tunneling.”
.
Your statement is incorrect, the Hamiltonian is not purely a classical concept.
.
In classical mechanics, the Hamiltonian is a function that describes the total energy of a system, including both kinetic and potential energy. In quantum mechanics, the Hamiltonian becomes a mathematical operator, known as the Hamiltonian operator, which acts on a system’s wave function to describe its energy and behavior. The Hamiltonian operator is used to solve the Schrödinger equation, which determines the probability distribution of a particle in a given potential field and is critical to predicting Quantum Tunneling.
.
Here is a direct quote from Chapter 3, Neutron Scatter Physics and Differential Cross Sections by Jay Theodore Cremer, Jr. (https://www.sciencedirect.com/science/article/pii/B9780123969699000033)
.
“The Hamiltonian operator Hψ=Eψ, extracts eigenvalue E from eigenfunction ψ, in which ψ represents the state of a system and E its energy. The expression Hψ=Eψ is Schrodinger’s time-independent equation.”
.
Here is another direct quote from Chapter 8 – Quantum Optics by Avijit Lahiri. (https://www.sciencedirect.com/science/article/pii/B9780128053577000083)
.
“In general, the state of a quantum system changes, or evolves, with time as in the case of a classical system, where this time evolution constitutes the dynamics of the system. As in the classical case, the dynamics of a closed quantum system is governed by its Hamiltonian, where the Hamiltonian is an operator corresponding to its energy, as indicated in Section 8.3.8. Let us consider a closed system with Hamiltonian Ĥ whose state at time t, assumed to be a pure one, is described by the vector |ψ(t)〉of unit norm. Then the time evolution of the state is governed by the equation (8.52) ihd/dt |ψ(t)⟩ = H|ψ(t)⟩, where d/dt |ψ(t)⟩ gives the rate of change of the state vector at time t. This is a first-order differential equation in the Hilbert space, which on integration gives the state at any time t in terms of the state at any initial time t0, and is referred to as the Schrödinger equation for the system under consideration. The time evolution is of a trivial nature if the initial state |ψ(t0)〉 is an energy eigenstate of the system—that is, if it satisfies H|ψ(t0)⟩ = E|ψ(t0)⟩, (8.53) where E is an eigenvalue of the Hamiltonian.”
.
I don’t know if all the equations will come through accurately in this chat posting system but you can lookup the articles and the equations are there.
.
So I hope you can see and anyone reading our little posts can see that you are the one who is misinformed and it is you that “clearly have no idea what you are talking about”.
.
Interestingly, I think a good response from you would have been to point out that quantum tunneling actually has some real applications and is not just a theoretical phenomenon and plays a role in things like Flash memory and Scanning Tunneling Microscopy. So predicting the ability or probability of an electron to make it to an unlikely place has utility.
.
In any case, I don’t think there is much use to continuing this conversation. It is totally fine if we disagree, and I hope you see that this post is not insulting you as your posts insulted me. I wish you the best.
John, after your wonderful work here, I somehow noted intriguing incentives to wake up every morning with thought of new discovery in micro-world or rediscovery of forgotten discoveries by those who are no longer with us – we are mortal, you know. So, making long story short, idea is to widen R&D in this field of physics. While we isolated geographicaly and resources are concentrated in main stream institutions, curiocity still works and delivers. So far, what I consider my understanding of the theory (that you kindliy introduced), while I delve into more deep R&D, is this (thanks to poe.com for free of charge ai assistance):
1. Space as an Elastic Solid.
Elastic Medium: space as a ghostly elastic solid, where the fabric of space can stretch and deform. This medium supports wave-like phenomena, allowing for the propagation of energy and information.
Photon as Solitons: In this model, photons are considered solitons of pulses of fabric of space traveling through this elastic space.
2. Photon Collisions and Pair Production.
High-Energy Collisions: When two high-energy photons collide within this elastic medium, they can interact in a way that produces electron-positron pairs. This process can be visualized as the elastic medium responding to the energy of the photons, creating disturbances that manifest as new particle pairs.
Knot-like Standing Waves: The resulting electron and positron could be imagined as a knot-like standing wave in the elastic medium. This standing wave reflects the topological properties of the space, where the energy of the photons creates stable configurations.
3. Electromagnetic Field as a Manifestation.
EM Field Representation: The electromagnetic (EM) field can be viewed as the collective behavior of these knot-like solitons. As photons interact and form pairs, the resulting structure in the elastic medium gives rise to electromagnetic phenomena.
Field Dynamics: The dynamics of the EM field could be described by the interactions of these solitonic structures, where the behavior of light, charge, and other electromagnetic interactions emerge from the underlying elastic medium’s properties.
4. Topological Aspects.
Knots and Topology: The knot-like configurations imply a topological structure in the field. This can lead to different particle states and interactions based on the nature of the knots formed by the solitons.
Quantum States: The stability of these knots might correspond to quantized states of the electromagnetic field, aligning with the concept of quantized energy levels in quantum mechanics.
5. Implications for Particle Physics.
Particle Interaction: This model opens up new ways to think about particle interactions, where the elasticity of space and the knot-like nature of particles influence scattering processes and decay mechanisms.
Emergent Phenomena: Just as solitons can arise from nonlinear interactions, complex phenomena such as mass, charge, and force could emerge from the interactions of these fundamental solitonic structures.
6 Conclusion.
This framework of an elastic medium where photons are solitons and interacting photons produce knot-like standing waves offers a rich ground for exploring the micro-world. Such ideas inspire new directions in theoretical physics and deepen our understanding of the universe.
Tony, I am very very interested in hearing John’s responses to your “take” on his writings re the underlying nature of things. I feel like your summation has helped me understand John’s ideas more clearly, but maybe John has clarifications to make? Yours is a recent post that I hope the Physics Detective sees soon and replies to.
Michael/Tony: utmost apologies. I somehow missed this. I will respond in detail tomorrow.
Thanks Tony.
1.Space as an Elastic Solid. Yes, I think space is an elastic solid. But maybe it has some non-Newtonian fluid properties too. For example a photon is a soliton pulse, but if a zillion photons converge at one location, the result will be a gravitational field, which I think of as a density gradient in space. That means the photon somehow conveys space. You will appreciate from What energy is that at the fundamental level, I can’t distinguish space and energy.
2. Photon Collisions and Pair Production. I would put it more simply, in that pair production is where two photons on linear paths are converted into two photons on curved closed paths. The only stable massive particles are electrons and protons plus their antiparticles. So the curved closed path can be in the form of a chiral trivial knot or a chiral trefoil knot. Yes, these look like standing waves. Standing wave, standing field. Annihilation is the opposite of pair production, wherein two opposite knots cancel and the photons are released. Things like pions may be released instead, but these are short-lived configurations which decay to photons, electrons, and neutrinos.
3. Electromagnetic Field as a Manifestation. I’d say the important point about the electromagnetic field is that it is frame-dragged space. Or twisted space if you prefer. A particle like an electron is an optical-vortex “spinor” structure, part of which is twisted space extending outwards. It will move towards and around another optical-vortex spinor with the opposite chirality – a positron. If however the other spinor has the same chirality, the two particles move apart. It’s like this: counter rotating vortices attract, co-rotating vortices repel. PS: I’m putting together some PowerPoint slides on electromagnetism and will post it up on Wednesday.
4. Topological Aspects. I’d go a little further and say a topological structure in space is what a field is. I’d also say the knots are stable, and the quantized states are related to gear-like motions of opposite structures that are attracted towards one another but can’t annihilate because they aren’t exactly opposite. The simplest case is the hydrogen atom. The electron and the proton are attracted to one another, but there’s no lock-and-key fit to result in annihilation.
5. Implications for Particle Physics.Yes, I think this concept opens up new ways to think about particle interactions. Especially since messenger particles do not exist. See Cathryn Carson’s papers for details. Yes, mass and charge are emergent. Mass is just resistance to acceleration for a wave in a closed path. Charge is just the topological result of wrapping the sinusoidal electromagnetic wave into a spin ½ spinor configuration. Do try it with sinusoidal paper strips. Force is not some magical mysterious action at a distance; in for example a gravitational field, the electron drives itself downwards due to a downward refraction of the horizontal component of the wave in a closed path.
6 Conclusion. Agreed. Can I add that a neutrino seems to be more like a photon than an electron. It’s like a photon with no transverse component. Can I also add that the neutron seems to be a close-couple electron-proton combination like Rutherford said. There’s a neutrino twist in the spin statistics, but otherwise electron capture does what it says on the tin. Beta decay is the opposite, which means W bosons are superfluous. I’m happy to talk on Zoom etc if you wish.
John, based on your corrections, I think at least it will help make animated visualizations – visualizations is what is possible to do with little or no funds. At large, John, your work should be introduced to big pockets for investments in examples of proof of the theory. I look forward to enjoy your success and ours success as well
A thousand thanks Tony..