There’s a lot of articles about magnetic monopoles. See this for example: the hunt for magnetism’s elementary particle begins. It dates from 2016, and it’s by Avaneesh Pandey. He says this: “magnets, for reasons we still do not understand, seem to exist only in the form of dipoles – ones with a north and a south end. Break a bar of magnet into two, and you still do not get a magnetic monopole. Instead, you now have two smaller magnets, each with its north and south pole”. There’s a link to the paper on the arXiv with an impressive list of contributors, and very nice picture to help with the visualization:
 Image credit : Daniel Dominguez of the CERN media lab
Image credit : Daniel Dominguez of the CERN media lab
Pandey says electricity has its positive and negative charged particles, and asks how scientists can isolate “magnetism’s elementary particles – the monopoles”. He says they’ve remained infuriatingly elusive. You can find other articles such as mysterious monopole remains elusive. It dates from 2013, and it’s by Devin Powell. He says more or less the same thing: “In standard electromagnetic theory, isolated positive and negative electric charges exist, but magnetic poles always come in pairs”. He says to fix this asymmetry, Paul Dirac proposed the existence of magnetic monopoles. Another article is the hunt for the truest north. It dates from 2016, and it’s by Matthew Francis. He gives this quote: “The electric and magnetic forces are exactly the same force,” says Wendy Taylor of Canada’s York University. “Everything would be totally symmetric if there existed a magnetic monopole. There is a strong motivation by the beauty of the symmetry to expect that this particle exists”.
Symmetry
You see repeated references to symmetry when you read about monopoles. Search the Wikipedia monopoles article for symmetry or symmetric, and there’s 22 matches. The article refers to Maxwell’s equations, saying they provide for electric charges but not magnetic charges. And that except for this difference, the equations are “symmetric under the interchange of the electric and magnetic fields”. It then says you can write fully-symmetric Maxwell’s equations if you allow for the possibility of magnetic charges. This desire for symmetry drives physicists to search for magnetic monopoles. They say things like the existence of monopoles is “one of the safest bets that one can make about physics not yet seen”. There’s just one little problem: magnetic monopoles do not exist. Yes, you can contrive a very long solenoid, so that the other pole is out of sight and out of mind. And you can do something similar in condensed matter physics to create an effective magnetic monopole. But that’s not a real magnetic monopole. It isn’t what particle physicists have been hunting for with no success. I think that when you look closely at electromagnetism, you can appreciate why there’s been no success. Let’s start with a bar magnet.
The bar magnet
A bar magnet consists of a North pole and a South pole. It’s a dipole, not a monopole. At first glance one might think that breaking a magnet in half will yield two monopoles. But it won’t. In 1822 Ampère said magnetism was the result of electric currents circulating in planes perpendicular to the axis of the magnet. He said each particle of the magnet would be surrounded by a circular current. There’s a modern picture of such Ampèrian currents on Ampère and the history of electricity. It’s by Gérard Germain, from Physique Terminale C dating from 1983:
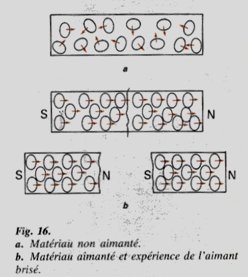 Image by Gérard Germain
Image by Gérard Germain
He depicted a non-magnetic material where the circulating currents – let’s call them “spinors” – are aligned in a variety of different directions. Underneath is a bar magnet where the spinors are all aligned the same way. Because of this there’s a North pole at one end and a South pole at the other. Hence when you break the magnet in half, each half still has a North pole at one end and a South pole at the other. Breaking the magnet doesn’t yield two monopoles. That’s because the North pole is merely the end from which the spin looks clockwise, and the South pole is merely the end from which the spin looks anticlockwise. Each half still has a North pole and a South pole, because the North pole is just looking at all the rotation from one direction, and the South pole is just looking at it from the other. To look at this more closely, let’s replace the bar magnet with a solenoid.
The solenoid
A solenoid has a magnetic field much like a bar magnet. Ampère invented the word solenoid in 1820. He said “if the spirals acted like magnets, it was because magnets owe their magnetism to electric currents in planes perpendicular to their axes”.
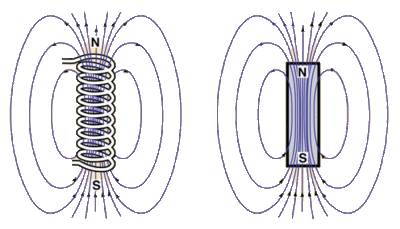 Image from Rod Nave’s hyperphysics
Image from Rod Nave’s hyperphysics
Of course a solenoid isn’t exactly the same as a bar magnet. A bar magnet doesn’t feature a helical current of electrons flowing around and around. But aligned electron spin produces the same result as the macroscopic motion of electrons, namely a magnetic dipole field. When you cut the solenoid in half then reinstate the current, it’s like breaking the bar magnet in half. You now have a shorter solenoid, with a North pole at one end and a South pole at the other. When you repeat this, you have an even shorter solenoid, still with a North pole at one end and a South pole at the other. Keep on repeating, and you end up with a single loop of wire.
The current loop
When you pass a current through a loop of wire, the result is a fairly simple magnetic field. It’s a dipole field. When the current’s going clockwise, we call the region above the loop the North pole, and we call the region below the loop the South pole:
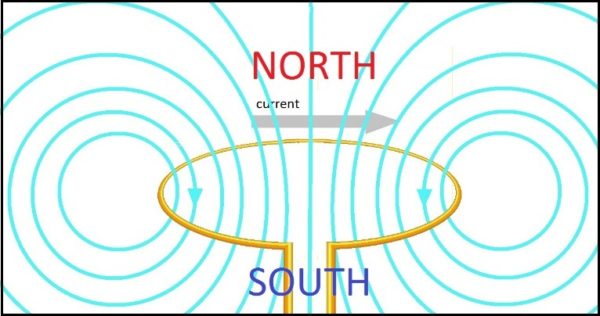
But note that the poles aren’t in the centre of the concentric circles. The poles are orthogonal to the concentric circles, because those circles are only depicting a slice through the magnetic field, which is toroidal. The poles are above and below the torus, in the middle of the loop. And just as there are no one-sided coins, there are no one-sided loops. There are no torii which have an above but no below. Slicing the loop in half horizontally won’t separate those poles. It will merely give you two sets of poles, like breaking the bar magnet in half. You don’t end up with a monopole. And nor do you end up with a monopole when you straighten the loop out.
The wire is not a monopole
At first glance the current-in-the-wire looks something like a magnetic monopole. It doesn’t have a dipole field. You depict it with just one set of concentric circles, using the right-hand rule. The field is actually cylindrical, but we typically depict a slice through it like so:
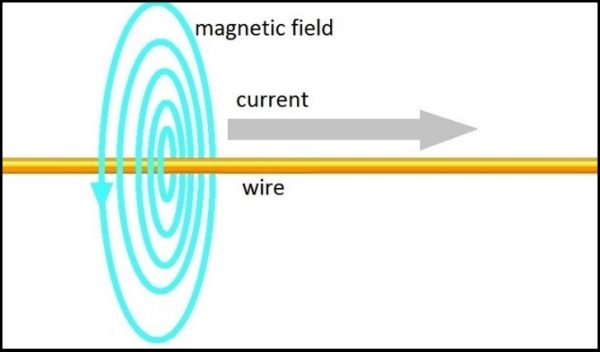
Note though that there is no pole at the centre of the concentric circles. Also note that you can’t point to a pole that’s orthogonal to the concentric circles. There is no place you can point to and say this is the North pole. Or the South pole. And yet we still have magnetism. Two wires with currents flowing the same way will attract one another. When they do, you might be tempted to say one’s a North pole and one’s a South pole. But the two wires are the same, and two North poles repel, they don’t attract. Ditto for two South poles. You only get repulsion when the two wires have currents flowing in the opposite directions. To achieve that you rotate one of the wires lengthwise through 180 degrees. That’s like flipping a bar magnet over lengthwise, swapping the North and South poles over. So it’s like one wire is a North pole and the other’s a South pole. But now the two wires repel. This is breaking the rules of North poles and South poles. We still have magnetism, all we’ve done is straightened out the current loop. But whilst the wire loop has a North pole and a South pole, a straight wire doesn’t have either. It’s more of a nopole than a monopole. So you won’t find a monopole here. Or anywhere else. To look at this more closely, I think the best thing to do is zoom in on the wire, and look at what it’s made of: charged particles.
The charged particles in the wire
The wire is made of copper. We have electrons that move and we have copper ions that don’t. Whilst a copper ion is far more complicated than an electron, it’s made of protons and neutrons. Since a free neutron will decay into a proton plus other things, let’s simplify the copper ions down to protons. Our wire is effectively a cylinder of electrons and protons, with the electrons moving from left to right. Each electron has a magnetic dipole field, as does each proton. Neither the electron nor the proton has a monopole field, for a very simple reason.
The electron
The electron can be likened to a tiny bar magnet, or a current loop. Obviously this is not conduction current, which is typically the macroscopic motion of electrons. Instead it’s displacement current, and it’s associated with a very real angular momentum, as evidenced by the Einstein-de Haas effect. As Feynman said: “If you look at the energy flow, you find that it just circulates around and around”. He was talking about the Poynting vector, in an example in which an electric charge and a magnet are at rest near each other:
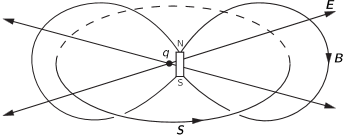 Figure 27-6 from The Feynman Lectures by Michael A Gottlieb and Rudolf Pfeiffer
Figure 27-6 from The Feynman Lectures by Michael A Gottlieb and Rudolf Pfeiffer
But what he didn’t say is that the electron itself is like the electric charge and the magnet. Or that the electron doesn’t have an electric field and a magnetic field. Instead it has an electromagnetic field. Maxwell unified electricity and magnetism. The field we’re dealing with is the electromagnetic field. It’s not totally unlike the gravitomagnetic field. I think you can best think of it as a “twist” field. Then when you move through it or it moves through you, it starts to look like a “turn” field. We don’t talk of rot for nothing, and rot isn’t short for rotor for nothing. Maxwell didn’t say this for nothing either: “a motion of translation along an axis cannot produce a rotation about that axis unless it meets with some special mechanism, like that of a screw”. He said it because the electromagnetic field has a “screw” nature. That’s why electromagnetic field interactions result in linear force and rotational force. When we only see linear force we talk of an electric field, and when we only see rotational force we talk of a magnetic field. But these are merely two aspects of the greater whole that is the electromagnetic field. To visualize it you have to combine radial electric field lines with concentric magnetic field lines, like this:
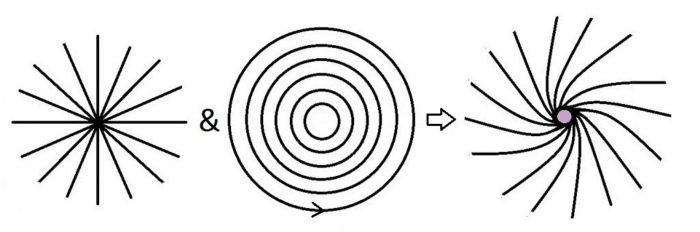
Only then do you get a sense of the electromagnetic field, which for some strange reason is never depicted. Only then do you get a sense of spinors and why electrons move the way that they do, and how a magnet works. Only then do you appreciate what Maxwell was saying in 1871: “electric currents are regarded as a species of translation, and magnetic force as depending on rotation”. And “when there is both convergence and curl, it will point in a spiral”:
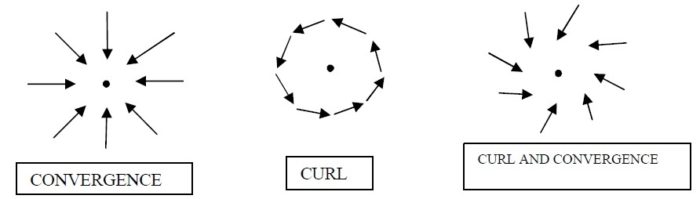 Image by James Clerk Maxwell
Image by James Clerk Maxwell
Then you appreciate why there are no magnetic monopoles. Because it takes two to tango, and linear electric force and rotational magnetic force is what you see when two “spinors” interact like counter-rotating vortices. If they have no initial relative motion, they move directly towards another. But if you throw one past the other, they move towards one another and around one another. Hence you cannot take the magnetic aspect away from the electron’s electromagnetic field to leave it with an electric field only. You cannot take the electric aspect away from the electron’s electromagnetic field to leave it with a magnetic field only. So the phrase electric charge is a misnomer, one that misses the whole point of Maxwell’s unification.
Why there are no magnetic monopoles
The electron doesn’t have an electric field, it has an electromagnetic field. So it doesn’t have an electric charge, it has an electromagnetic charge. So the whole idea of magnetic charge is misguided. It’s the wrong symmetry, a desire for beauty borne from a total lack of understanding of electromagnetism. It’s a castle in the air with no foundations. Hence hunting for magnetic monopoles is a waste of time. It’s a wild goose chase. It’s a fool’s errand. There are no magnetic monopoles because of the screw nature of electromagnetism, which is all about twist and turn. To make an electromagnetic field you twist space, and then you can move through it such that it looks like space is turning. Or it moves through you. Either way the result is a “rotor” field, with a North pole and a South pole, because the North pole is just looking at the rotation from one direction, and the South pole is just looking at it from the other. There are no one-sided coins, and there are no regions of space turning round and round like a ball in a socket. That’s what you’d need for a true magnetic monopole. There are no discontinuous spheres of rotating space, because space isn’t like that. Because it’s a continuum, like a gin-clear ghostly elastic solid that sustains transverse waves which can get wrapped and trapped in a closed spin ½ path. Instead there’s something akin to frame-dragging going on, where space is twisted, only in three dimensions, with curl and chirality. If there wasn’t, particles wouldn’t be charged particles. Magnetic monopoles do not exist, because if they did, there would be no such thing as charge.
PS: As a neutrino passes you by it’s a momentary magnetic monopole. But it isn’t a real magnetic monopole. A magnetic field is a “rotor” field, and there’s no continuous ongoing rotation.
PPS: if the whole universe was rotating, that would constitute a magnetic monopole of sorts. But as far as we can tell, it isn’t.
Never say never – what if every electric charge itself is magnetic monopole of sort, huh?
The darkest place is just under candlestick…
https://arxiv.org/ftp/physics/papers/0512/0512265.pdf
http://www.cybsoc.org/electron.pdf
Magnetic monopoles cannot exist within flat space-time only. But the space-time inside particles wouldn’t be quite flat…
Hi Zephir. I refer to those two papers in https://physicsdetective.com/the-electron/. Also see https://physicsdetective.com/the-photon/ where I talk about electromagnetism in terms of spatial curvature. The electron’s electromagnetic field is effectively a “twist” field. But if you moved through it, you might claim it to be a “turn” field – check out curl rot and rotor. But there are no regions of space that are actually rotating. That’s what you need for a magnetic monopole. So you won’t be finding any magnetic monopoles any time soon.
One-dimensional things (particles) should always look like mobius strip if you think about it https://imgur.com/HGdhceH
Iron is magnetic because its nucleus has two rings of 12 protons.
http://ferronuclear.blogspot.com/2017/06/iron-has-nucleus-with-two-loops-of.html
That looks interesting Alan. But some of the models have a lot of protons next to one another, and a lot of neutrons next to one another. That doesn’t feel right. See my article on the nuclear force.
John, iron itself is not allready magnetized, so what does happen to a piece of iron or similar metal that allows it to gain and then hold an elctromagnetic field/charge thus turning it into a magnet ? Remember, I am just a larger, hairier version of your granny.
You just get all the electron spins to line up. See https://physicsdetective.com/the-electron/ where I refer to the Barnett effect. You rotate an unmagnetized soft iron cylinder to magnetize it.
As a student under Luis Alvarez at UCB he convinced me to search. He got me 50,000manganese nodukes from the ocean, i flew a lead plate spark chamber on a westher balloon, after a while it dawned on i could do this forever. Went and got an MBA got rich instead.
Good for you Pete. Luis Alvarez did some good stuff. But I guess he was an experimentalist first and foremost, not some theory guy who knew all the fundamental physics. And hey, if you can get some student to look for free as it were, that’s maybe a good idea. Who is Nick Athens?
nice and good
Uh oh, I think I’ve been spammed!
Amazing, this is almost similar to what I’ve been thinking for some time too. I don’t think electromagnetic waves look like something with two-dimensional wavy “things” that run perpendicular or at 90 degree angle to each other but instead something like 3D lines that are spiraling or something like one of those individual double strand “ropes” that are viewed from their cross sections.
Mohamed, you might like What is a photon? and The photon?. I’m not sure that my description of an electromagnetic wave is totally correct, but I am sure that the orthogonal electric and magnetic wave description is totally incorrect.
Sorry what I mean by “something like one of those individual double strand “ropes” that are viewed from their cross sections” is this picture
When I originally commented I clicked the “Notify me when new comments are added” checkbox and now each time a comment is added
I get three emails with the same comment. Is there any way
you can remove people from that service? Many thanks!
Please use the contact form to tell me more.