Quantum Information Supremacy

Scott Aaronson is a Computer Science professor at the University of Texas at Austin. See his Wikipedia entry, which says he’s the founding director of UT Austin’s new Quantum Information Center. Aaronson is into quantum computing in a big way, and is a famous blogger on the subject. His blog is called Shtetl-Optimized, and one of his recent posts was called Quantum Information Supremacy. I take an interest in this sort of thing because I have a Computer Science degree, and I know a thing or two about fundamental physics. Hence I thought I’d take a look.

Demonstrating an unconditional separation between quantum and classical information resources

Aaronson’s Quantum Information Supremacy post is about a paper he co-wrote with ten other authors. It’s called Demonstrating an unconditional separation between quantum and classical information resources. Aaronson said he was thrilled about it, and that it’s based on a collaboration between UT Austin and a corporation called Quantinuum. He thanked his Austin colleagues William Kretschmer, Nick Hunter-Jones, and Sabee Grewal, saying Kretschmer led the theory and wrote much of the code, and Hunter-Jones and Sabee Grewal made important contributions too. He also thanked the team at Quantinuum “for recognizing a unique opportunity to test and showcase their cutting-edge hardware, and collaborating with us wild-eyed theorists to make it happen”. It would seem that Aaronson and his UT colleagues did the theoretical stuff, and the Quantinuum guys did the practical stuff. Whatever, Aaronson then gave the abstract of the paper:

Screenshot from the arXiv, see https://arxiv.org/abs/2509.07255

The abstract started by saying a longstanding goal in quantum information science is to demonstrate quantum computations that “cannot be feasibly reproduced on a classical computer”. It referred to this as called quantum advantage, saying such demonstrations mark major milestones. It also said said quantum advantage has previously been demonstrated through Bell tests and sampling experiments. However it qualified this by saying the Bell tests are not computationally difficult, and the “hardness” of the sampling experiments is unproven. It went on to say the current paper is about a better demonstration of quantum advantage realized on Quantinuum’s H1-1 trapped-ion quantum computer “operating at a median two-qubit partial-entangler fidelity of 99.941(7)%”. The abstract said the team constructed a task which would need between 62 and 382 bits of classical memory, and solved it using only 12 qubits. It then said this was the most direct evidence yet that quantum processors “can generate and manipulate entangled states of sufficient complexity to access the exponentiality of Hilbert space”. The abstract finished up saying “this form of quantum advantage – which we call quantum information supremacy – represents a new benchmark in quantum computing”. Aaronson then finished up his blog post saying he’d be happy to field questions about the paper in the comments section. There were 160 comments, which is good. What’s not so good is that many of them concerned the Many Worlds Interpretation which says we live in a multiverse, and superdeterminism which says we have no free will. Personally I find it strange that some people seem to prefer myth and mysticism to empirical science, but such is life.

A Hilbert space is an abstract mathematical space which is flat and Euclidean, but has more than three dimensions

The paper itself looks daunting, because it’s 42 pages long with 97 references. However as Aaronson pointed out to me in his comments, the main part of the paper is only 5 pages long, and the rest is supplementary material. Page 1 started by saying quantum theory postulates that “a system of n particles is represented by a vector in Hilbert space with exponentially many continuous parameters”. I should explain that a Hilbert space is an abstract mathematical space which is flat and Euclidean, but has more than three dimensions. In quantum computing a Hilbert space is said to have 2ⁿ dimensions where n is the number of qubits. The idea is that if you add one qubit you double the number of dimensions. The paper then said the goal of quantum computing is “to determine when and how this exponentiality can be harnessed to perform computations that are infeasible for classical computers”. It referred to Shor’s algorithm, which dates from 1994, and said skeptics think the exponential speedup it’s supposed to offer is not be achievable in practice.

Explanation of Shor’s algorithm by minno, see Reddit

It also said at the heart of the skepticism is the belief that “physically realizable quantum systems cannot be engineered to exploit the exponential dimensionality of Hilbert space”. It added that reasons for this skepticism range from minor issues of decoherence and error accumulation, to the major issue of whether quantum mechanics is complete. The latter strikes a chord with me. The paper also said the question of whether Hilbert space is physical has been debated since the early days of quantum mechanics. As per the abstract, it then referred to Bell tests and sampling experiments, and then asked two questions: whether it’s possible to experimentally demonstrate an unconditional quantum advantage, and “whether a quantum device can perform a computation that establishes the exponential dimensionality of Hilbert space as a physically accessible resource”. It then said the answer to both questions of these questions was yes. I was surprised at that myself. I think it’s one thing to say qubits offer an advantage over bits, but something else to say it’s because Hilbert space is real.

This yields an unconditional separation between quantum and classical information resources

But no matter. On page 2 the paper said the team used “the tools of one-way communication complexity” to formulate a computational task for which a classical algorithm requires at least 62 bits of memory. It went on to say the team solved the task with only 12 qubits, and that “this yields an unconditional separation between quantum and classical information resources”. It also said “our result provides direct evidence that today’s quantum hardware can prepare quantum states of sufficient complexity to access the exponentiality of Hilbert space”. Again, there’s that claim that Hilbert space is somehow real. I’m all for thinking outside the box and breaking the rules. For example I think there’s a way to get round conservation of charge. So I’m all for solving tasks in novel ways. For example if you had a tea tray with two sliding sides, you could pour 400 ball bearings on to the tray, then you could jiggle and slide to find that 20 is a factor of 400:

Slide-side tray factoring depiction by me

This would be an analogue computer of sorts, and if you could contrive it via trapped-ion electronics to emulate Shor’s theorem, that’s great. Then since quantum means how much, I’m happy if you want to call it a a Quantum Processing Unit (QPU) or a quantum computer. But please don’t bullshit me with infinite-dimensional Hilbert space. I wasn’t born yesterday.

From Communication Complexity to Quantum Information Supremacy

The paper then talked about a “one-way communication task” wherein Alice and Bob “wish to jointly compute a function on their inputs”. Alice receives an input string x whilst Bob receives an input string y. Then Alice sends message mₓ to Bob, who performs a computation to output a correct result f(x, y) = z. The goal is to minimize the length of mₓ. The paper said the challenge “is to identify tasks for which the communication required is significantly smaller than the input size” and “the use of a quantum message |ψₓ⟩ can provably reduce the amount of communication required by an exponential factor”. To paraphrase, Alice could pass her full input string to Bob, but that’s akin to classical computing. The idea is that a shorter message demonstrates a quantum advantage.

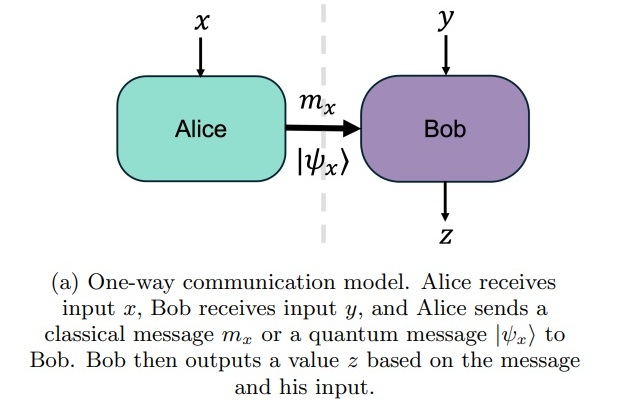Figure 1 part (a) from Demonstrating an unconditional separation between quantum and classical information resources

However the paper then changed tack to say instead of Alice and Bob separated in space, they’re in the same place at two different times t₀ and t₁. It said “in this analogy, the communication bottleneck between Alice and Bob becomes a limitation on the amount of information that the device can transmit across the temporal boundary”. My brow furrowed at that, because I’ve previously done some detective work on time. If I have some information right now, I don’t have to transmit it to myself across some “temporal boundary”. There is no temporal boundary. I already have the information. I just sit and wait. Or maybe I don’t wait at all.

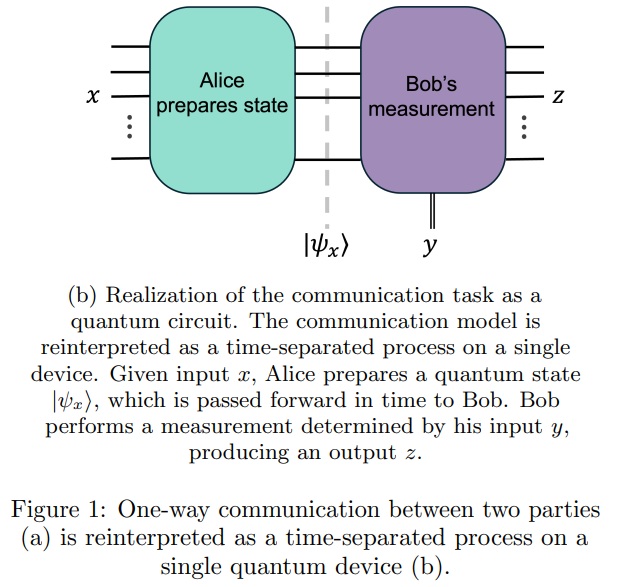 Figure 1 part (a) from Demonstrating an unconditional separation between quantum and classical information resources

The paper asserts that “the basic premise of quantum information supremacy is to recast a quantum advantage in communication as an advantage in storage”. The trouble with that is that now there is no Alice and Bob. It’s just Alice. Alice receives string x, prepares message |ψₓ⟩, then combines it with a second string y to produce result z. Nevertheless, the idea is that a “quantum resource” needs n qubits to store the message, whilst a “classical resource” needs exponentially more bits. For an analogy, consider the trinary bit, also known as a trit. It can have three states -1, 0, or 1. If you stored your message in trits instead of bits, you’d need fewer trits than bits. And so on.

Improved Quantum-Classical Separations

Rather surprisingly the paper then backtracked from storage to communication. It said quantum advantage in one-way communication has long been known, but “separations are insufficiently strong to achieve nontrivial quantum information supremacy”. I don’t buy that. A spatial separation is a damn sight stronger than a non-existent “temporal boundary”. The paper then said “to remedy this, our chief theoretical contribution is a new one-way communication problem that can be solved using n qubits of quantum communication”. That’s as opposed to circa 2ⁿ bits of digital communication. The paper described this new problem as “a distributed version of linear cross-entropy benchmarking (XEB)”. Look it up. XEB is not some real world problem related to factoring or cryptography. It’s “a method for assessing the performance of quantum processors”. That’s not good. Also note that it “has been used as a test for procedures simulating quantum circuits”. Simulating quantum circuits isn’t good either.

A linear cross-entropy benchmarking fidelity is a metric used to evaluate the performance of quantum circuit simulators

On page 3 the paper said “the task asks Alice, who holds a quantum state, and Bob, who holds a quantum measurement, to work together to produce bit strings that are high-probability outputs of Bob’s measurement on Alice’s state”. High probability? What happened to the correct result? The paper then said Alice’s input x is a classical description of some n-qubit quantum state |ψₓ⟩, and Bob’s input y, which is really Alice’s second input, is “a description of an n-qubit measurement in the form of a circuit Uᵧ”. The task is to produce length-n bit strings z “whose distribution, over many repetitions of the problem, achieves high linear cross-entropy benchmarking fidelity”. So Alice gets a digital input, turns it into qubit states, then since there is no Bob, Alice combines that with another digital input to produces a digital output. This is then repeated many times to yield a “high linear cross-entropy benchmarking fidelity”. Which can be spoofed. And is a metric used to evaluate the performance of quantum circuit simulators. Not only that, but the proof is not some clear-cut demonstration like me wiring up a minitron with fewer DILICS than Tom Kilburn thought possible. It’s statistical.

Let Alice’s state be sampled from the Haar measure over n-qubit states

Hence my eyes narrowed as I read on. And I quote: “The quantum protocol for this task is simple: Alice’s message to Bob is |ψₓ⟩, and Bob processes the state by applying Uᵧ and measuring in the computational basis. Assuming that the state |ψₓ⟩ and circuit Uᵧ exhibit sufficiently strong anticoncentration, the FXEB achieved by implementation on a quantum device is well-approximated by the fidelity of the device”. A quantum protocol is a set of rules and methods used in quantum communication. A computational basis refers to the set of standard states used to represent qubits in quantum computing. An anticoncentration refers to how evenly a quantum state spreads across all possible outcomes. Do keep up boys and girls. There’s then a reference to a 7-page 2019 Nature paper Quantum supremacy using a programmable superconducting processor, and to a 3-page appendix H2:

Screenshot from page 34 of Demonstrating an unconditional separation between quantum and classical information resources

Then there’s this: “Theorem 1: Let Alice’s state be sampled from the Haar measure over n-qubit states, and let Bob’s measurement be sampled independently from the uniform distribution over n-qubit Clifford measurements. Any classical protocol that achieves average FXEB ≥ ε with respect to this input distribution must use at least min{Ω(ε²2ⁿ), ε2^n−O(√n)} bits of information”. I’m sure you all understand that, don’t you boys and girls? Ah, I see you’re all nodding. Right then, you boy, Powell, step up here and explain it to the rest of the class. LOL, I know where this is going. Anyway, after that there’s then a reference to the 7-page appendix E4, a reference to the 3-page appendix G, and just as I expected, a graph:

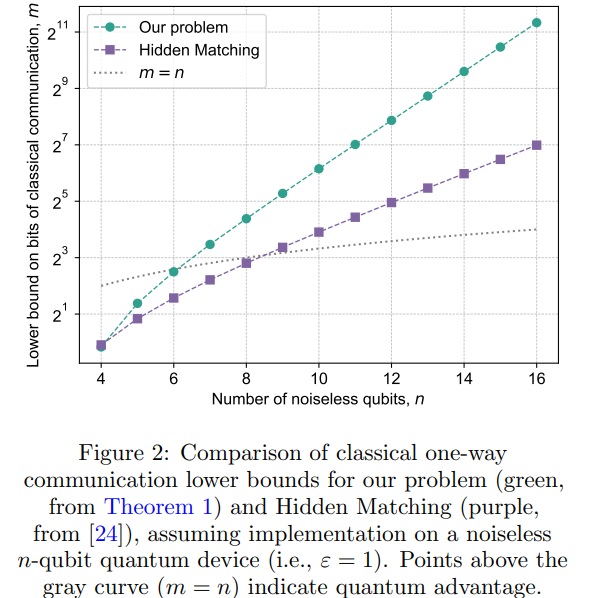Figure 2 from Demonstrating an unconditional separation between quantum and classical information resources

For the cherry on top, the paper said theorem 1 “witnesses a quantum advantage with as few as n = 7 qubits, compared to n = 9 for the best previously-known separation”. That’s fewer than the number of terms in the theorem 1 expression. But don’t worry boys and girls, because complementing theorem 1, a classical protocol would need circa ε2ⁿ/ln(2)²n bits, and it’s all explained in the 5-page appendix F. What’s not to like?

Implementation and Experimental Results

After that, the paper talked about the implementation and the results. It said they used the Quantinuum H1-1 quantum computer “which provides 20 fully connected trapped-ion qubits”. It referred to Quantum Charge Coupled Device (QCCD) architecture. This is said to be analogous to a CCD camera. The CCD camera “stores and processes imaging information as movable electrical charges in coupled pixels”. The QCCD “stores quantum information in the internal state of ions that are transported between different processing zones using dynamic electromagnetic fields”. See the Wikipedia article on trapped-ion computers for background information. Also see appendix H where you can read about Ytterbium qubit ions and Barium coolant ions, plus hyperfine states along with Bloch sphere rotations and fluorescence measurement. The moot point is that the Quantinuum H1-1 quantum computer has 20 qubits. Meanwhile there are 256 gigabytes of storage on my Samsung A35 phone. That’s over 2 trillion bits. Spot the difference.

Generating exact Haar-random states is infeasible

The paper talked about the H1-1 two-qubit gates being a source of errors, along with memory errors incurred during qubit idling, transport, and cooling. There are of course no such issues in digital computers. The paper also talked about noise, then Haar-random states derived from a Haar measure. It said generating exact Haar-random states is infeasible on near term quantum hardware, so they “variationally train a parameterized quantum circuit to approximate Alice’s Haar-random message”. The paper then it talked about “brickwork ansatz” circuit consisting of one-qubit gates and two-qubit gates, with 86 two-qubit layers in total. The one-qubit gates are purple, the two-qubit gates are green:

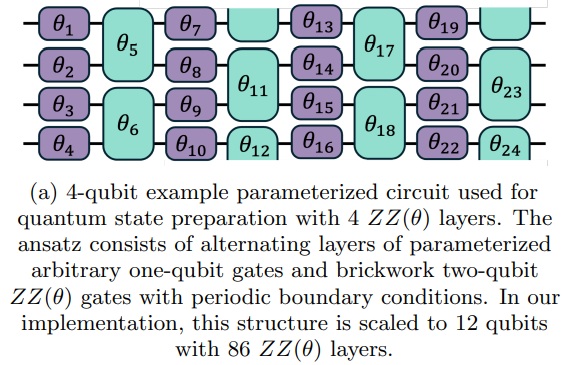Figure 3 part (a) from Demonstrating an unconditional separation between quantum and classical information resources

It then talks about Clifford measurement. As I’m sure you all known that’s a type of randomized quantum measurement that uses a circuit of Clifford gates to estimate properties of a quantum system. The paper also talks about classical control bits used by a field-programmable gate array (FPGA), which is a classical processor. This uses the classical control bits to trigger QPU gate operations via RF-modulated laser pulses routed through optical fibres.

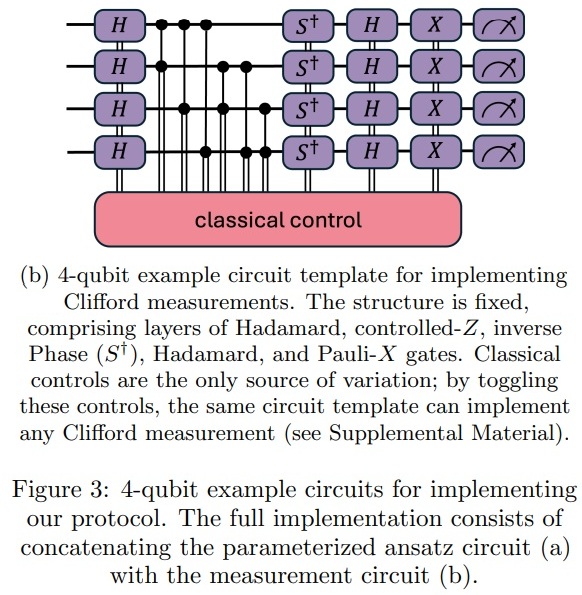Figure 3 part (b) from Demonstrating an unconditional separation between quantum and classical information resources

As Craig Gidney pointed out in the comments, these control bits are not included in the 7-qubit count, and it’s impossible to build a quantum computer without a control system. He also pointed out that 5 bits of storage is sufficient to evaluate complex functions by using enormously long sequences of instructions. But never mind such minutiae, the paper then said the experiment requires a source of true randomness to generate inputs x and y, otherwise theorem 1 doesn’t hold. This doesn’t sit well with what they said about training “a parameterized quantum circuit to approximate Alice’s Haar-random message”. The paper also said the experiment achieved an XEB fidelity ε of 0.427 computed from 10,000 independent trials. It then said “applying theorem 1 with n = 12 and ε = 0.427 implies that any classical protocol achieving the same average score would require at least 78 bits of memory”. The paper then talks about five standard errors, which is similar to the fabulous Higgs boson’s famous five sigma. It said if this was applied, then 62 bits would be needed.

Discussion and Future Work

The final section of the paper is a round-up. The authors said “we performed a task using 12 qubits on Quantinuum’s H1-1 trapped-ion quantum computer, for which any classical protocol achieving comparable performance provably requires at least 62 bits of memory”. They said this establishes “an unconditional experimental separation between quantum and classical information resources”. They also said their results are provable and permanent, and that their competitors have not properly demonstrated quantum advantage. They also referred to the first Bell test experiments, saying they contained loopholes that were only closed in later experiments. Then they said “our experiment is subject to similar caveats that future work may address or eliminate”. They went on to say a skeptic could say that the experiment “did not maintain a true temporal separation between Alice and Bob’s inputs”. Or challenge whether the QPU truly realizes a 12-qubit Hilbert space. Or whether a highly-entangled 12-qubit state is a low-entanglement state in a larger space.

The Emperor’s New Clothes.

What they didn’t say is that a skeptic would point out that the abstract says the team constructed a task and solved it using only 12 qubits, but that’s not actually what they did. Or that a skeptic would point out that there is no Bob, so there is no communication. But there are lies, damn lies, and then there are statistics. And that a 20-qubit experiment should provide scientific evidence, and should not rely upon a mathematical “proof”. Especially when the latter is comprised of five theorems concreted together into a 20-page Westeros wall of defensive mathematical handwaving:

Screenshot from page 19 of Demonstrating an unconditional separation between quantum and classical information resources

A skeptic would point out that there are such things as blarney, bullshit, sophistry, obscurantism, and moonshine. A skeptic would take you through the history and point out that Bell cooked up up a smoke-and-mirrors mathematical “proof” using probabilities adding up to one, then used this to claim that classical physics must yield a straight-line result rather than a cosine curve. A skeptic would point out that the cos² θ is there because Malus’s Law applies when you send photons through polarizers A and B regardless of whether the light goes through them like →→ or like this ←→. A skeptic would point out that the Nobel Bell tests performed by Clauser and Freedman and by Aspect et al, used cascade photons that were emitted at different times, and so were not entangled at all. Hence a skeptic would point out that there is no quantum entanglement. Then he’d tell you a horror story about quantum computing and the quantum quacks, and fairy tales about quantum echoes and The Emperor’s New Clothes. All together now boys and girls: the king is in the altogether, the altogether, the altogether, he’s altogether as naked as the day that he was born.