In physics, there is something called Malus’s law. It’s named after Étienne-Louis Malus, whose name is one of 72 names on the Eiffel Tower. It dates from way back, to 1809, and it gives the intensity of polarized light passing through an ideal polarizer:
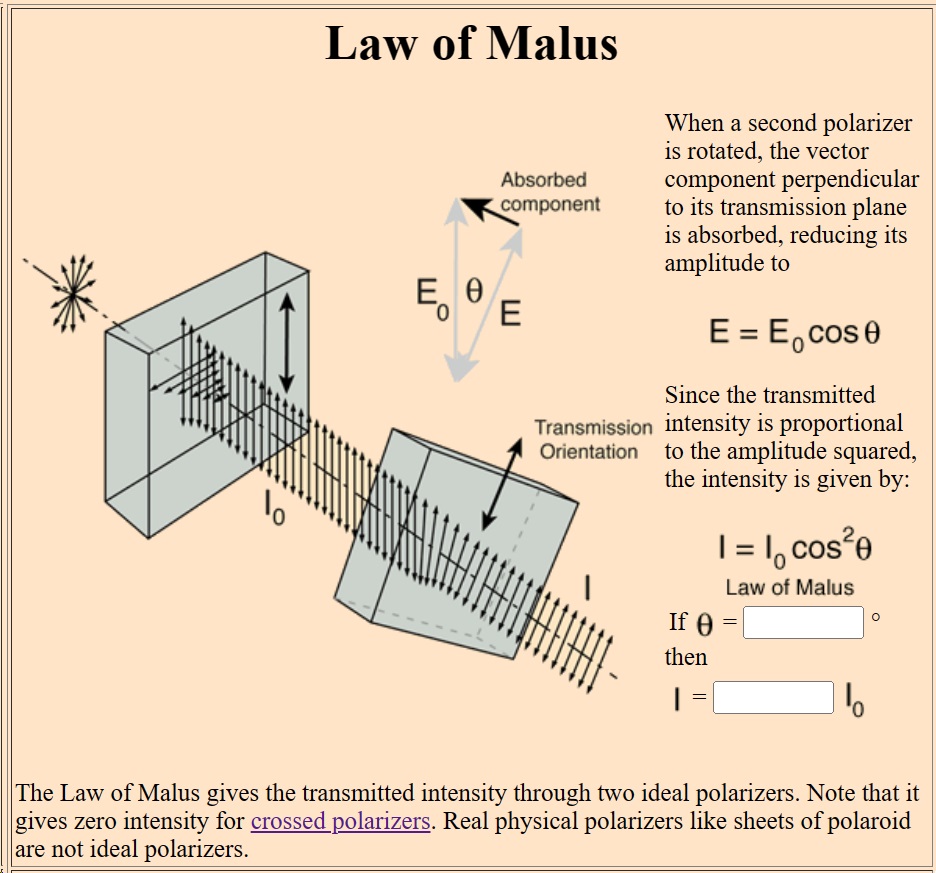 Malus’s law image from Rod Nave’s most excellent hyperphysics website
Malus’s law image from Rod Nave’s most excellent hyperphysics website
This intensity is given as I = I₀ cos² θ, where I₀ is the intensity of the light that has passed through an initial polarizer, and θ is the angle between the initial polarizer and the second polarizer. If you had a pair of perfect polarizers at your disposal, you could conduct experiments to measure the transmitted light for a variety of angles as follows:
When θ is 0°, all the light that got through the first polarizer gets through the second polarizer: cos 0° is 1, and 1² is 1.
When θ is 22.5°, more light gets through than you might expect: cos 22.5° is 0.923 and 0.923² is 0.85.
When θ is 45°, half the light gets through as you might expect: cos 45° is 0.707 and 0.707² is 0.5.
When θ is 67.5°, less light gets through than you might expect: cos 67.5° is 0.382, and 0.382² is 0.146.
When θ is 90°, none of the light gets through: cos 90° is 0, and 0² is 0.
You can rotate the second polarizer by intermediate angles to get more data points, and you can then rotate it the other way to get a set of data points for negative angles. Then you could plot a curve like this:
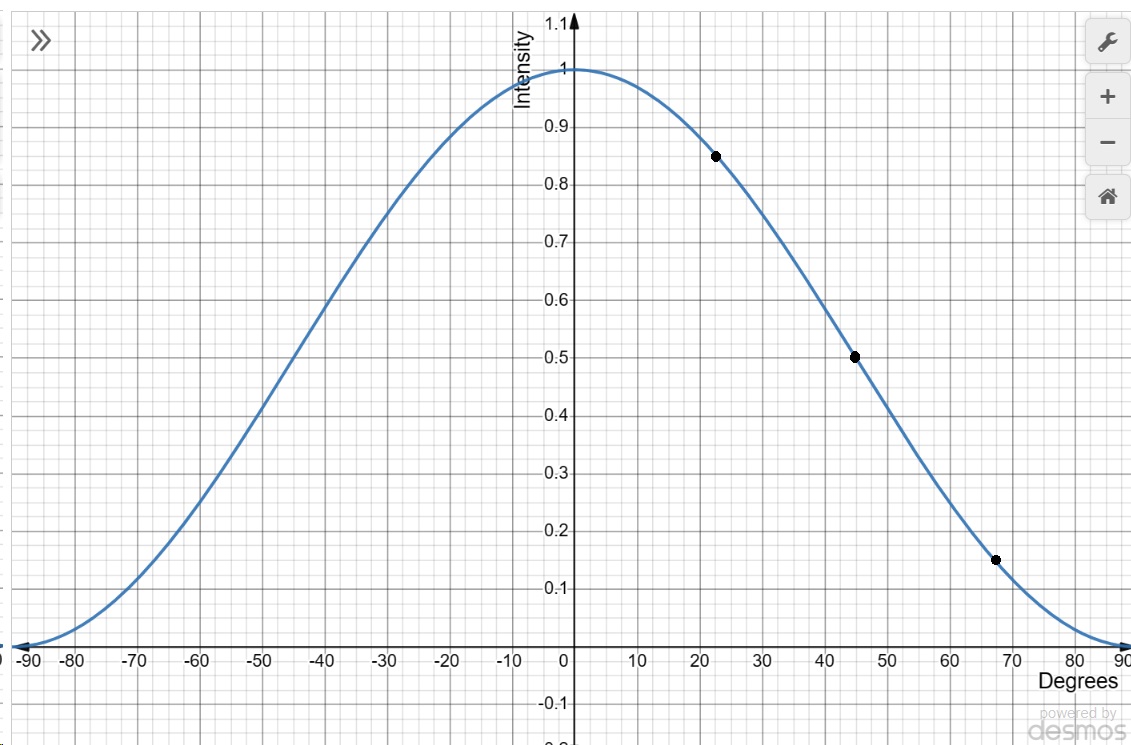 Graph plotted by me using Graph Plotter (transum.org), thank you John Tranter
Graph plotted by me using Graph Plotter (transum.org), thank you John Tranter
It’s not a straight line, it’s a cosine-like curve. As to why, it’s because a polarizing filter isn’t just a filter. We know this from the three-polarizer “paradox” which is sometimes described as a creepy quantum effect. Or as something wonderful and mysterious and spooky that illustrates Dirac’s 1930 explanation of the quantum superposition of states. It isn’t a paradox, and nor is it in any way creepy or quantum or wonderful. Or mysterious or spooky. It’s simple physics. A polarizing filter doesn’t just filter, it also rotates the light passing through it. When you have two polarizers at 90° to one another, none of the light gets through. But when you put a third polarizer between them at 45° to the first, it lets half the light through and rotates it. Then the third polarizer is at 45° to the second, and that lets half the light through again, and rotates it again:
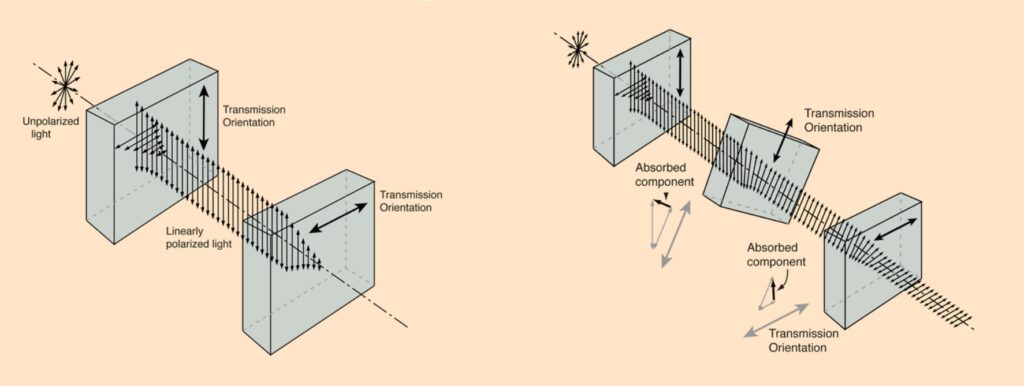 Crossed polarizer images from Rod Nave’s hyperphysics
Crossed polarizer images from Rod Nave’s hyperphysics
Note that light consists of individual photons. These have an energy of E=hc/λ, where h is Planck’s constant, c is the speed of light, and λ is the photon wavelength. Photons have a wavelength because they are waves, not billiard-ball particles. They have a “soliton” nature in that they don’t spread out or dissipate, and they can be detected and therefore counted. If a photon made it through the first polarizer, then the likelihood of detecting that photon passing through the second polarizer is related to the transmitted intensity I = I₀ cos² θ. Also note that it doesn’t matter which way the photon goes through the polarizer. What that means is that you could place your light source to the left of polarizers A and B and count the photons that go through both polarizers, or you place your light source in between polarizers A and B and count the photons that go through both polarizers:
 Simple image drawn by me showing the Malus’s Law scenario on the left and the Bell Test scenario on the right
Simple image drawn by me showing the Malus’s Law scenario on the left and the Bell Test scenario on the right
The former is the Malus’s Law scenario, the latter is the Bell Test scenario. In either case the light source emits photon pairs with the same polarization, which is a random polarization. In either case half the photons pass through polarizer A regardless of its orientation. In the Malus’s Law scenario cos² θ of these photons then pass through polarizer B, which means ½ cos² θ photons pass through both A and B. In the Bell Test scenario we also have half the photons passing through polarizer B regardless of its orientation. However the coincidence between A and B diminishes as we increase the angular difference θ between A and B. By how much?
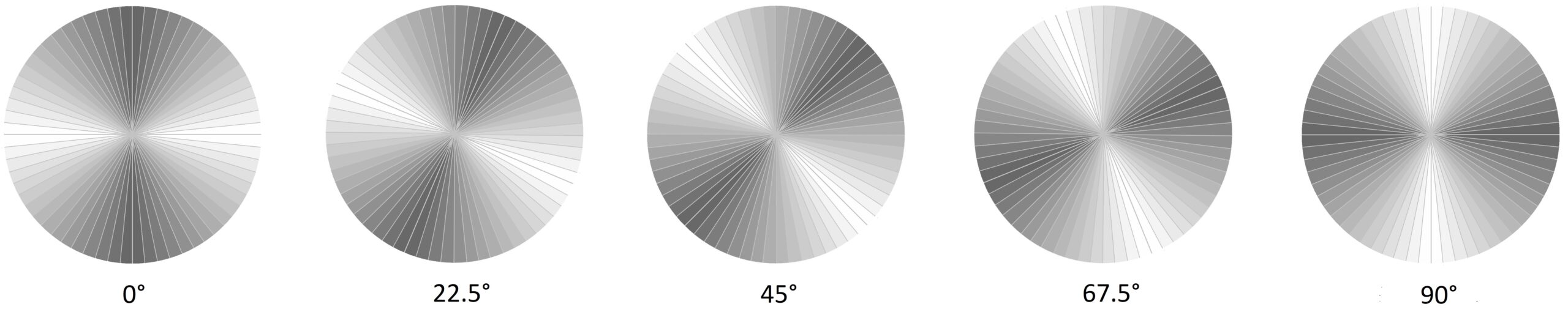 Shaded polygons by me based on a 32-sided polygon at Englishbix
Shaded polygons by me based on a 32-sided polygon at Englishbix
Check out the Wikipedia article on Aspect’s experiment. It refers to two-channel polarizers wherein “the result of each polarizer’s measurement can be (+) or (−) according to whether the measured polarization is parallel or perpendicular to the polarizer’s angle of measurement”. The article goes on to refer to two polarizers oriented at angles α and β, and then says that in quantum mechanics P++(α, β) = P–(α, β) = ½ cos²(α – β). It’s the same as the Malus Law scenario. There’s a picture of it on page 27 of Alain Aspect’s 2004 paper Bell’s Theorem: The Naive View of an Experimentalist:
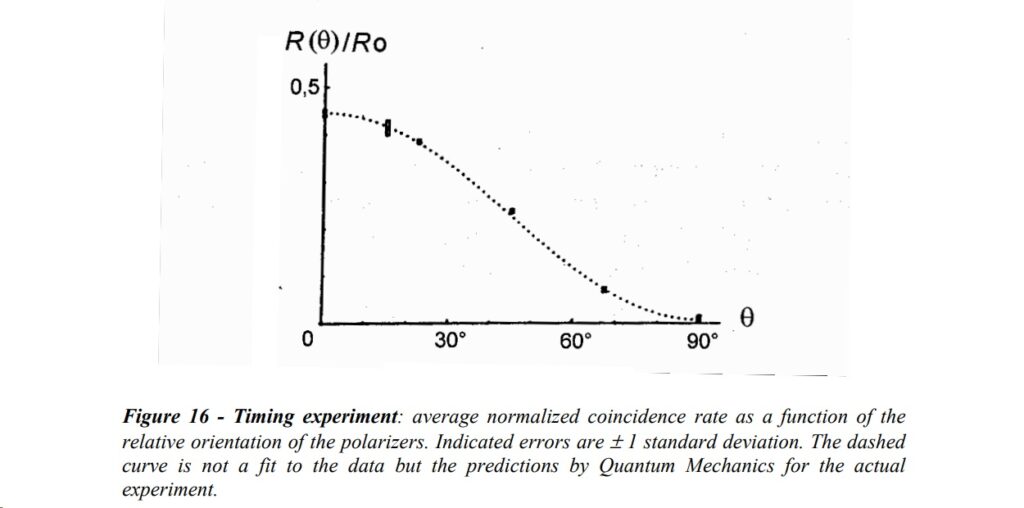 Image by Alain Aspect
Image by Alain Aspect
The Bell Test experiment was first performed by John Clauser and the late Stuart Freedman in 1972. Clauser shared the 2022 Nobel prize in physics for what is said to be the first experimental demonstration of quantum entanglement. The other prize winners were of course Alain Aspect and Anton Zeilinger, who performed further experiments which are said to have closed off “loopholes”, and demonstrated that spooky action at a distance indeed occurs. The idea is that when you measure the polarization of local photon A, you instantly collapse the polarization state of remote photon B, which was previously indeterminate. This is regardless of the distance between A and B.
 Image from Tech Explorist, see a new method for generating quantum-entangled photons
Image from Tech Explorist, see a new method for generating quantum-entangled photons
To recap, quantum entanglement began in 1935 with the EPR paper. That’s where Albert Einstein, Boris Podolsky, and Nathan Rosen said quantum mechanics must be incomplete because it predicts a system in two different states at the same time. Later that year Niels Bohr replied saying spooky action at a distance could occur. Then Erwin Schrödinger came up with a paper where he talked of entanglement, a paper where he used his famous cat to ridicule the two-state situation, and a paper saying he found spooky action at a distance to be repugnant. He and people like Einstein preferred the idea of “hidden variables”, which meant there was something we didn’t know. Nothing much happened after that until 1952 when David Bohm came up with two hidden variables papers which talked about the spooky action at a distance. He also came up with the EPRB experiment in 1957. Then in 1964 John Stuart Bell came up with papers On the Problem of Hidden Variables in Quantum Mechanics and On the Einstein Podolsky Rosen Paradox. Bell said the issue was resolved in the way Einstein would have liked least, via a difficult-to-follow mathematical “proof” which is usually called Bell’s theorem. The nub of it is a probability expression called Bell’s inequality. It’s given in different forms, but in his EPR paper Bell gave it as:
![]()
Here a, b, and c refer to polarization angle vectors, and P denotes “expectation values” which represent probabilities for angular differences. It says 1 plus a bc term must be greater than or equal to an ab term minus an ac term. It sounds reasonable, because in mathematics and physics, probabilities add up to 1. I can draw it for you like this:
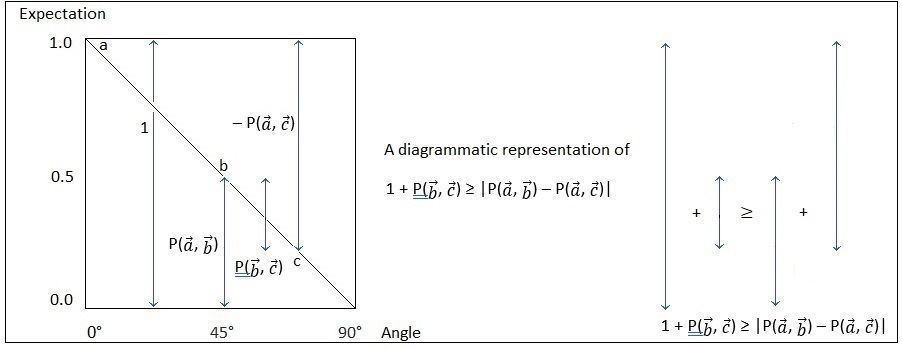
When you understand it, you can see that it’s a fairly simple statement about the sum of probabilities. But then you understand that it isn’t reasonable at all. You realise that it’s deliberately confusing, and deliberately misleading. It’s the mathematical equivalent of smoke-and-mirrors. Bell used this to make the grand claim that a “classical prediction” yields a straight-line hidden-variables result. Then, despite Malus’s law, he made the even grander claim that if polarizer experiments did not match this, they would prove that there are no hidden variables, and that instantaneous spooky action at a distance must be occurring. This is why Bell’s inequality is usually illustrated with a picture like the one below by on page 9 of Alain Aspect’s 2004 paper::
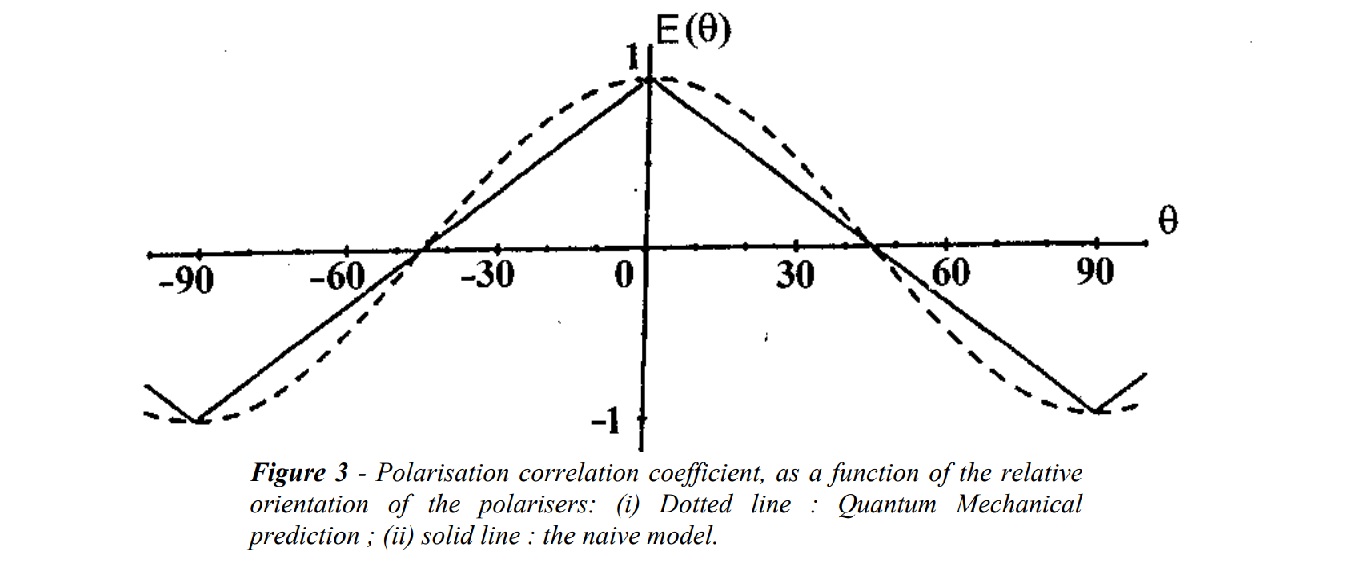 Image by Alain Aspect
Image by Alain Aspect
Classical physics is said to predict the straight-line result, and the cosine-like curve is said to be proof positive of spooky action at a distance. It’s the same cosine-like curve as the Malus’s law curve above, albeit with a different y axis. The curve is there because the local polarizer alters the polarization of the local photon, not the remote photon. Don’t think Aspect made a mistake with this. He even referred to Malus’s law in his 2004 paper. The Wikipedia article on Bell’s theorem featured a similar straight-line depiction by Richard Gill. There’s also a Stanford article which says this: “In Bell’s toy model, correlations fall off linearly with the angle between the device axes”. On top of that, you can see essentially the same thing in the Wikipedia article on Bell’s theorem:

What that says is that vectors a and b are at 90° to one another, vector c is at a 45° angle to both of them, and P is a correlation. When you correlate a and b, you get a result that’s zero. That’s cos 90°. Correlate a and c, or b and c, and you get a result that’s –√2/2, which is –0.707. That’s cos 45°. The claim is then that 0.707 is not less than or equal to 1 – 0.707 = 0.293, and therefore “there is no local hidden variable model that can reproduce the predictions of quantum mechanics”. But this is what we see with polarizing filters and Malus’s law. Not only that, but Clauser and Freedman’s photons were “cascade” photons emitted 5 nanoseconds apart with wavelengths of 581 nanometres and 406 nanometres. A photon travels 1.5 metres in 5 nanoseconds. By the time the second photon was emitted, the first photon was through the polarizer. Those photons weren’t even entangled. Aspect used the same cascade, so his photons weren’t entangled either. This is why Al Kracklauer was talking about Malus’s law twenty years ago. And why Dean L Mamas wrote a paper in 2021 called Bell tests explained by classical optics without quantum entanglement. He said “The observed cosine dependence in the data is commonly attributed to quantum mechanics; however, the cosine behavior can be attributed simply to the geometry of classical optics with no need for quantum mechanics”. It’s true. The inconvenient truth is that the cosine-like experimental results that are said to prove the existence of quantum entanglement, are simply the results of polarizers that rotate the photons passing through. It’s similar for spin ½ particles where the so-called entanglement is said to be measured by Stern-Gerlach magnets. Bell accidently revealed this in his 1980 paper on Bertlmann’s Socks And The Nature Of Reality. His figure 6 depicted the rotation:
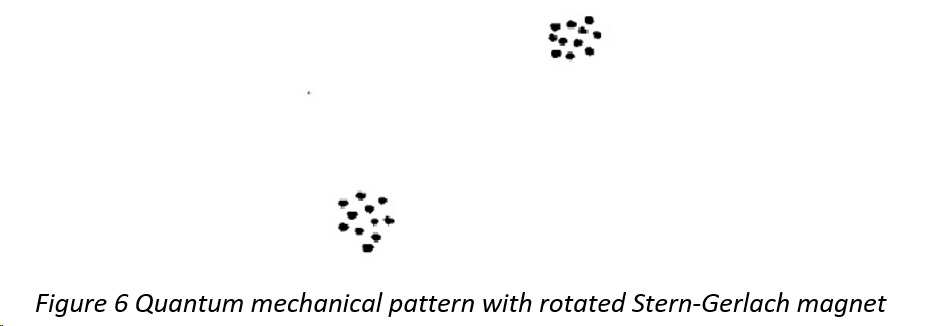
Bell worked at CERN. It’s just not credible that nobody at CERN knew about Malus’s law. It’s just not credible that nobody in contemporary quantum physics knows about Malus’s law. Ditto for the Nobel committee. They all know about Malus’s law. They’re all academics, the sort of people who stamp on free speech and who censor anything they don’t like. The sort of people who wallow in wokery and antisemitism. The sort of people who live a life of ease on the public purse whilst morphing their business model from education to immigration. They all know about Malus’s Law, but they continue to peddle the myth and mystery of quantum entanglement because it brings in the funding for quantum computing. That’s the quantum computing that has never ever delivered anything, and never ever will. Such is the sorry state of academia today.
“What that means is that you could place your light source to the left of polarizers A and B and count the photons that go through both polarizers, or you place your light source in between polarizers A and B and count the photons that go through both polarizers”
.
This is obviously not true. In the left picture you’re rotating each photon twice, while in the right picture you’re rotating each photon only once. Given two angles A and B with B>=A, and given the same photon with polarization θ, the probability of going through both polarizers in the first case is cos² (A-θ) cos² (B-A), while in the second case it is cos² (A-θ) cos² (B-θ). The two probabilities are the same only if B-A=B-θ or A=θ, that is filter A is aligned with the photon and does nothing on it. In every other case the two probabilities are different. Unfortunately in experiments the probability always depends on B-A, irrespective of the initial polarization θ.
That’s not right I’m afraid Sandra. Take a look at the first image. Malus’s Law features one absorbed component. Not a component absorbed by the first polarizer followed by a component absorbed by the second polariser. The first polarizer is merely giving you a set of photons with the same polarization at the centre point of the left image. In the right image you start with two photons with the same polarization at the centre point. In either situation your plot of results gives a cosine-like curve. Not a straight line. Bell, Clauser, Aspect, and Zeilinger must surely have known this. Aspect even referred to Malus’s Law in https://arxiv.org/abs/quant-ph/0402001.
“ Malus’s Law features one absorbed component.”
.
One for each polarizer, yes. Consecutive polarizers have a multiplicative effect, as you can see in Rod Nave’s image.
.
“The first polarizer is merely giving you a set of photons with the same polarization at the centre point of the left image.”
.
So you’re saying A sets the angle θ for the photon in the left image, and we consider only photons from this point, hence the final probability only depends on B? This means you’re effectively considering only 1 polarizer. Why not start with a polarized beam in the first place? What does this have to do with entanglement experiments?
.
“In the right image you start with two photons with the same polarization at the centre point.”
.
You’re then comparing a system with only 1 significant polarizer (left image) with one with 2 indipendent polarizer (right image). Alternatively, you’re saying A influences θ in both cases, which obviously implies spooky action.
Sandra, you’re in italics:
.
One for each polarizer, yes. Consecutive polarizers have a multiplicative effect, as you can see in Rod Nave’s image.
.
That’s true, but note that I₀ is determined after the light has passed through the first polarizer A.
.
So you’re saying A sets the angle θ for the photon in the left image, and we consider only photons from this point, hence the final probability only depends on B?
.
Not quite. In the left image some of the emitted photons will not get through A, but we don’t know about them, and can’t include them in our probability. So we have to start after the photons have made it through A. Then we use Malus’s law to say I = I₀ cos² θ, which gives us a probability for the photons that passed through A passing through B. We plot this as a cosine-like curve.
.
This means you’re effectively considering only 1 polarizer. Why not start with a polarized beam in the first place?
.
I think it might clarify matters to start with a polarized beam. Imagine we have vertically-polarized photons as per Rod Nave’s “Law of Malus” drawing. We emit two photons A and B in opposite directions, one towards polarizer A, the other towards polarizer B. Polarizer A stays vertical, so the A photon always gets through. We alter the angle of B, such that the chances of the B photon getting through varies with Malus’s law. The detection rate is proportional to the intensity I = I₀ cos² θ, so for coincident detections we plot a cosine-like curve. Now rotate polarizer A by 45°. The chance of photon A getting through polarizer A is now half what it was. We alter the angle of B, such that the chances of the B photon getting through varies with Malus’s law. The detection rate is proportional to the intensity I = I₀ cos² θ, so for coincident detections we plot the same cosine-like curve. We were never going to plot a straight-line slope as we varied the angles between the polarizers.
.
What does this have to do with entanglement experiments?
.
The experiments yield cosine-like curves because a polarizer rotates a photon’s polarization. When you “measure” the local photon you are altering the polarization of the local photon, not the remote photon. As for entanglement experiments, Clauser and Freedman’s photons were not entangled, they were emitted 5 nanoseconds apart. They merely had the same polarization, and we have one polarizer at each end of their experiment. It was the same for Aspect et al, who initially used the same calcium cascade.
.
You’re then comparing a system with only 1 significant polarizer (left image) with one with 2 independent polarizer (right image). Alternatively, you’re saying A influences θ in both cases, which obviously implies spooky action.
.
I’m saying A influences θ for the A photon, and B influences θ for the B photon. I’m saying A does not influence θ for the B photon, and B does not influence θ for the A photon. I’ve made some amendments to the article to try to make this clearer.
Sandra states that the probabilities won’t add up to one while the Detective says those won’t be detected because of the way classical polarizers work. This reminds me of the fair sampling loophole that has been closed using electron spin, https://arxiv.org/abs/1508.05949, clearly showing that the first measured spin is actually instantly (spookily) transferred to the other electron.
.
This of course was already all shown a long time ago via the CSHS game experiments, for which there are no local hidden variable possibilities for.
.
I think of this for electron spins, take two gamma rays and make an electron-positron pair. Assume one gamma ray goes to create an electron and the other created a positron (and it was the collision that initiated this change). However, sometimes its half of each gamma ray that creates an electron and half of each creates a positron, but the halves are still connected. Yes, now we have a magical nonlocal instant connection even if the electron and positron get separated. Now when you measure the spin of one, that connection instantly makes the other the opposite. And this is what entanglement is, if you believe in realism.
Doug, please have a read of my articles on the electron and the positron. The electron and the positron have the opposite spin. That’s why one is an electron and one is a positron. If their spins were the same, they’d both be electrons, or they’d both be positrons. I’ll reply later on the CHSH game and the paper. And to other comments. As ever I am pushed for time.
Doug: I read the paper at https://arxiv.org/abs/1508.05949. To summarize, they used optical pumping to “initialize” the spins of two electrons in two different locations A and B. Each electron emits photons. Then when “two photons from A and B arrive simultaneously at location C” and they’re indistinguishable, they say the two electrons are entangled via entanglement swapping. Then “a fast switch transmits only one out of two different microwave pulses” to the electrons, and they have an optical spin read-out for each along the ±Z-axis or along the ±X-axis. So they fire photons at electrons which emit photons. Then when the electrons are emitting photons with the same characteristics, they quickly fire further photons at the electrons which emit further photons used for a spin readout. Then there’s a correlation between the spin readout results which violates the CHSH-Bell inequality with S = 2.30. I’m sorry Doug, but this is a long way removed from the photons going through polarizers, and let’s face it, those electrons have never met. They are said to be entangled via the photons they emitted, but that’s a whole new can of worms. And surely, one would expect electrons emitting photons with similar characteristics to have similar spins? I’m sorry, but I see no conclusive evidence for instantaneous action at a distance here. And I’m sorry, I’ve run out of time. I will have to comment on the CHSH game, which involves 0s and 1s and ANDs and XORs, another day.
Interesting, I should have read it more thoroughly myself. I do find the entanglement with particles that have never met to be quite odd. Thanks for taking the time to go through it, I think you will find the CSHS game more interesting and convincing!
Cheers,
Doug
Doug: re the CHSH game, I think Scott Aaronson gave a fair explanation of it here. IMHO the important line is this: “Given that Alice measured her qubit already, Bob’s qubit collapsed to the |0> state”. That’s indirectly sending information, which isn’t supposed to happen via quantum entanglement. See https://sci-hub.st/10.1038/4661053a. There’s more about the game on stack exchange in Proof of optimality for CHSH game classical strategy. That gives S = A₁B₁ + A₁B₂ + A₂B₁ − A₂B₂, and says |⟨S⟩|≤2|. But there’s https://arxiv.org/abs/1901.07050 where Robert B Griffiths said (like Joy Christian) that A and B don’t commute, hence ⟨S⟩ = 2√2, “in obvious violation of the inequality”. So I’d say winning the game doesn’t prove the spooky action at a distance. I searched the internet on CHSH fake “loophole” and found there’s plenty of debate about all this. Sorry this isn’t a great reply, but I’m pushed for time at the moment.
“Half the photons headed towards A pass through A. Half the photons headed towards B pass through B. But as you increase θ, you reduce the probability of both photons in a pair passing through their respective polarizers”
.
Assuming any initial polarization of the photon, what is the chance both go through when θ (the angle between detectors) is zero, for a single pair? What is the average chance over multiple pairs (say, 360, one pair for each degree)?
What if instead the angle θ is 90°?
.
You could add the answer to these simple questions to your article to prove your point.
.
.
“The scenarios are so similar that it just doesn’t leave room for spooky action at a distance.”
.
They are not similar at all, and I’ve already explained why in detail. It is your own suggestion that leaves only room for spooky action, it is not a model I adopted. Since I don’t believe in spooky action, that means as it is I also believe your suggestion to be wrong.
.
.
As for other articles, I think I’d be interested in your take about the Hubble tension, the recent developments and the DESI controversy. For a fast review, https://youtu.be/yKmPJmaeP8A?si=zO_JvKRM_RhRBjQl
Sandra,
.
How can you not believe in the spooky action at a distance?
If it’s higher dimensional, the action still occurs over a distance does it not?
.
I would be very interested how your idea could get rid of the spooky action.
Doug: i dont think it is higher dimensional. The result of measurements depends exclusively on local effects. I do think though that the properties of the space we live in are not what they look at first glance, like an ant thinking the surface of a balloon is flat. I’ve already made a reply with a more thorough explanation.
Thanks for the reply, still super interesting stuff, alas, I also have work and did not have time to delve too much into all these different debates/viewpoints. However, I don’t the buy people saying they can beat the game (>75%) classically (no spookiness), because then, you could make a simulation of it, or show how to do it. .
.
It is exchanging information, just random information that cannot be validated until both people send their bits back to a judge via normal speed of light, so you still can’t transmit FTL.
.
Apparently there’s even a bound (Tsirelson’s bound) that says if you beat the game by just a few more percent, then you could do FTL communication, .. but alas, nobody has done that yet. So no FTL yet.
All interesting stuff, Doug. As somebody who has a computer science degree and has watched the excellent progress in computing over the years, the word “yet” strikes a chord. My phone has more computer power than NASA had when they put a man on the moon. But despite the fact that people have been talking about quantum computers for over forty years, they still haven’t delivered. I think they never will, because there is no quantum entanglement. I would be very interested to hear what somebody like Scott Aaronson thought about that. Perhaps you could ask him about it? I doubt that you would get a clear evidential answer, he was extremely unpleasant to Joy Christian about it. See this article.
.
Can I add that I don’t see a big issue with FTL communication. I say that because seismic waves give us an example of longitudinal waves propagating faster than transverse waves, and light waves are transverse waves. However I don’t think such FTL communication would be instant. It might be twice the speed of light, but not a million times faster.
“We were never going to plot a straight-line slope as we varied the angles between the polarizers.”
.
I think this needs further discussion to clear up some misconceptions. The straight line curve is just one of the possible classical hidden variable models you can build, specifically so that the results give you the same answer for angles 0, angles 45 and angles 180 as the quantum prediction. You can build other hidden variable models that give you more cosine-like curves, but they will always be different from the quantum prediction, for example by their amplitude: instead of going up to probability 1 at 0°, it might go up to 0.5 (meaning when the two polarizers are at the same angle they will both pass or both not pass only 50% of the time instead of 100%). Another thing I really want to point out is that real experiment done with polarizers include two beams instead of one, one vertical and one horizontal: this is necessary because we are not able to detect photons that didn’t make it through with only one beam. Though this doesn’t necessarily change how we discuss the problem, it’s just a nitpick.
.
“We emit two photons A and B in opposite directions, one towards polarizer A, the other towards polarizer B. Polarizer A stays vertical, so the A photon always gets through. We alter the angle of B, such that the chances of the B photon getting through varies with Malus’s law.”
.
Sure, but here we are specifically assuming that the emitted photon’s polarization is aligned with A, that is vertical. No problem so far.
.
“Now rotate polarizer A by 45°. The chance of photon A getting through polarizer A is now half what it was.”
.
Don’t forget that we are calculating coincidence counts. Now the chance to go through A is 0.5 instead of 1; this multiplies the chance of going through B, which follows malus law. The chance now is proportional to 0.5*cos² θ, if we keep assuming a vertically polarized photon. Note how when we have A at 45° and rotate B also at 45° (meaning they are now at the same angle) the total chance is 0.5*0.5 = 0.25, which is different from 1: 100% coincidence rate is always the actual result for same-angle measurements. The total curve you obtain in this setup is cosine-like, but it doesn’t reach the correct values for certain angles. It is not a curve that depends on the angle difference between A and B, but instead one that depends on each angle’s deviation from the vertical. Since the system is rotational symmetric, you can start with any direction of polarization for the initial photon and it will give you always this result.
Sandra, again you’re in italics:
.
I think this needs further discussion to clear up some misconceptions. The straight line curve is just one of the possible classical hidden variable models you can build
.
It’s what Bell’s inequality predicted. Bell did not predict one cosine-like curve for the classical prediction, and another cosine-like for the quantum prediction. To be blunt, he tried to persuade his audience that we were dealing with straight-line probabilities adding up to 1 as opposed to those cosine-like curves. Do you dispute this?
.
specifically so that the results give you the same answer for angles 0, angles 45 and angles 180 as the quantum prediction. You can build other hidden variable models that give you more cosine-like curves, but they will always be different from the quantum prediction, for example by their amplitude: instead of going up to probability 1 at 0°, it might go up to 0.5
.
As per my 45° scenario in the previous comment, if you fire vertically-polarized photons at a polarizer angled at 45° to that vertical, half of them will make it through the polarizer. This will happen whether the polarizer is the A polarizer to the left, or the B polarizer to the right.
.
(meaning when the two polarizers are at the same angle they will both pass or both not pass only 50% of the time instead of 100%).
.
Again as per my previous comment, if they don’t both pass through, there is no coincident detection, so we don’t know about them.
.
Another thing I really want to point out is that real experiment done with polarizers include two beams instead of one, one vertical and one horizontal: this is necessary because we are not able to detect photons that didn’t make it through with only one beam. Though this doesn’t necessarily change how we discuss the problem, it’s just a nitpick.
.
Noted, no problem.
.
Don’t forget that we are calculating coincidence counts. Now the chance to go through A is 0.5 instead of 1; this multiplies the chance of going through B, which follows malus law. The chance now is proportional to 0.5*cos² θ, if we keep assuming a vertically polarized photon. Note how when we have A at 45° and rotate B also at 45° (meaning they are now at the same angle) the total chance is 0.5*0.5 = 0.25, which is different from 1: 100% coincidence rate is always the actual result for same-angle measurements.
.
As above. If they don’t both pass through there is no coincident detection, so we don’t know about them.
.
The total curve you obtain in this setup is cosine-like, but it doesn’t reach the correct values for certain angles. It is not a curve that depends on the angle difference between A and B, but instead one that depends on each angle’s deviation from the vertical. Since the system is rotational symmetric, you can start with any direction of polarization for the initial photon and it will give you always this result.
.
The moot point is this: if you send vertically-polarized photons towards A and B at say 1 photon per second, and then if you vary the angles of A and B, then at both A and B you will observe that Malus’s law applies. You will not see that it does not. You will see cosine curves for both A and B. What then is your evidence that what happens at A alters what happens at B? Some “symmetry of coincidence”, for want of a better phrase, is not enough. If a photon makes it through A, then its mirror-image photon will make it through B.
The long range weather forecast for Monday, April 8th Eclipse is : 70°F., partly cloudy. Got my ancient VHS video camera together, other cameras, tracking plots, and especially proper PPE eye protection all together. Next to-do are stocking up on beer, snacks, and music play lists.
Let’s hope for favorable photo conditions. PARTY ON JOHN !
Have fun Greg. I have an electronic welding helmet that I’d be wearing for something like that. By the by, thinking of those dancing motherships I was telling you about, in addition to the beer, perhaps you could bung some biscuits, beans, and bacon in the boot of your car. And a couple of other bits and pieces, if you catch my drift. Just in case it turns into a situation like this: https://www.youtube.com/watch?v=cEGZhDzy4G4. LOL!
LOL ! As an retired bus driver, the racing of the family Volvo in reverse hit especially close to home! Like most of us, I’ve read or watched literally dozens upon dozens of first contact stories. So, my best guess is : there is at least a 50/50 chance of hostile invasion. Better mathematical minds such as Sandra or Doug should be able to come up with a better betting line? Talk about probabilities and statistical analysis.
🙂 I prefer a stick shift awd subie, but maybe a Volvo would fair better.
.
Far as I can tell there is basically no data at all on any of the parameters needed to calculate any of this stuff (chance of aliens existing and building spaceships). I find the first hand accounts convincing, but, no data and there are cameras everywhere… Maybe Avi Loeb’s new detection array (Galileo project) will pick up something interesting. Or maybe project Starshot will get some data if it actually gets launched and hits alpha centauri, .. or if the NASA solar gravitational lens telescope idea actually is deployed and works, we could image the exoplanets at high resolution and see a city.
.
Until then, if I had some money I would bet that there won’t be first contact in ‘x’ years, and then if there isn’t I get the money. While if there is first contact, the new tech we get from aliens will make the bet meaningless, if you even remember to ask me for it while there will be more interesting things like aliens to think about
.
😉
“It’s what Bell’s inequality predicted. Bell did not predict one cosine-like curve for the classical prediction, and another cosine-like for the quantum prediction.”
.
Bell’s inequality is specifically a statement about the best we can do with the type of hidden variable theory Bell envisioned. That is, the best you can do is make the theory perfectly agree at 3 angles, and the resulting plot is a straight line. He never implied other “less efficient” options did not exist. As I said, you can come up with something (within the simple assumptions Bell made) that plots a cosine curve: the resulting plot will in general agree less with the quantum prediction than the straight line. This is what the <= in the inequality means. Your proposal of simply using Malus' law is exactly of this kind.
.
This might be a bit convoluted for a text answer, but here's a concrete example: let's say we calculate the coincidence rate for polarizers A at 22.5° off the vertical, and B at 45° off the vertical. The test photon is assumed to be vertically polarized as a hidden variable. In the straight-line model, we expect 75% chance for it to go through A, and 50% for B, amounting to a total chance of around 38%. In the cosine model, you have 85% for A and still 50 for B, for a total of 43%. Still far from the experimental 85%, but it sure looks like cosine is better right? Well, remember this is only for the vertical photon case. If you change up the polarization of the photon and average out the results, the straight line is actually a better predictor. For example, rotating the photon by 30° would make angle A 52.5° and B 75°, whose respective chances are 42% and 17% (it follows from a simple linear proportion). In the straight-line model the chance has now gone down to (0.42*0.17)=~7% while the cosine plot has gone to cos^2(52.5)*cos^2(75)=~2%, now worse than the straight-line model. This is basically a manual version of the R^2 fit function you find in excel.
.
If you want an imperfect visual picture, it's a bit like imagining that straight line to be a string: you can relax the string and curve it to try and fit it with the quantum cosine curve, but doing that will necessarily compromise the overall % agreement.
.
.
"As above. If they don’t both pass through there is no coincident detection, so we don’t know about them."
.
You can easily have occurrences where only one passes. If the polarizers are at the same angle and you see a photon in B, when you check A and find no photon has passed you violate the 100% coincidence rate (bar detection loopholes, which have also been ruled out by experiments in 2015 if I'm not mistaken). I mentioned 25% of both passing through just for convenience; the same % applies to both being blocked, A being blocked with B passing, and A passing with B being blocked. The four options add up to 1, as they should. The problem is, this is not what occurs in experiments: we NEVER see one going through and the other not for same-angle polarizers (again, bar detection loopholes).
Sandra, apologies for the delay. I’m pushed for time at the moment. Again you’re in italics:
.
Bell’s inequality is specifically a statement about the best we can do with the type of hidden variable theory Bell envisioned. That is, the best you can do is make the theory perfectly agree at 3 angles, and the resulting plot is a straight line. He never implied other “less efficient” options did not exist.
.
Perhaps not. But I think he worked very hard to frame his argument using probabilities, knowing that they sum to 1 in a straight-line fashion, in order to rule out any option other than spooky action at a distance. I’d say he was trying to make a name for himself by saying “Einstein was wrong”, and I cannot believe that nobody at CERN told him about Malus’s law or the three-polarizer puzzle.
.
As I said, you can come up with something (within the simple assumptions Bell made) that plots a cosine curve: the resulting plot will in general agree less with the quantum prediction than the straight line. This is what the <= in the inequality means. Your proposal of simply using Malus' law is exactly of this kind.
.
The point remains that we repeatedly see the claim that a cosine-like curve is proof positive of spooky action at a distance, when it isn’t.
.
This might be a bit convoluted for a text answer, but here’s a concrete example: let’s say we calculate the coincidence rate for polarizers A at 22.5° off the vertical, and B at 45° off the vertical. The test photon is assumed to be vertically polarized as a hidden variable. In the straight-line model, we expect 75% chance for it to go through A, and 50% for B, amounting to a total chance of around 38%. In the cosine model, you have 85% for A and still 50 for B, for a total of 43%. Still far from the experimental 85%, but it sure looks like cosine is better right?
.
Yes, the cosine is better, but do note that there’s an issue with your experimental 85% in that it contradicts Malus’s law. If you split a million vertically-polarized photons each into two, and send one half toward polarizer A at 22.5° off the vertical, and the other half toward polarizer B at 45° off the vertical, you will not get 850,000 coincidences.
.
Well, remember this is only for the vertical photon case. If you change up the polarization of the photon and average out the results, the straight line is actually a better predictor. For example, rotating the photon by 30° would make angle A 52.5° and B 75°, whose respective chances are 42% and 17% (it follows from a simple linear proportion). In the straight-line model the chance has now gone down to (0.42*0.17)=~7% while the cosine plot has gone to cos^2(52.5)*cos^2(75)=~2%, now worse than the straight-line model. This is basically a manual version of the R^2 fit function you find in excel.
.
Again the above applies. You will not send photons through polarizer A and find that Malus’s law is not holding because you have another polarizer at B.
.
If you want an imperfect visual picture, it’s a bit like imagining that straight line to be a string: you can relax the string and curve it to try and fit it with the quantum cosine curve, but doing that will necessarily compromise the overall % agreement.
.
Noted.
.
You can easily have occurrences where only one passes. If the polarizers are at the same angle and you see a photon in B, when you check A and find no photon has passed you violate the 100% coincidence rate (bar detection loopholes, which have also been ruled out by experiments in 2015 if I’m not mistaken). I mentioned 25% of both passing through just for convenience; the same % applies to both being blocked, A being blocked with B passing, and A passing with B being blocked. The four options add up to 1, as they should. The problem is, this is not what occurs in experiments: we NEVER see one going through and the other not for same-angle polarizers (again, bar detection loopholes).
.
Please give a reference for the detection loopholes being ruled out by experiments in 2015. It sounds as if this is important for our conversation.
“Please give a reference for the detection loopholes being ruled out by experiments in 2015”
.
https://arxiv.org/abs/1508.05949
.
This was followed by other 2 experiments according to Wikipedia,
.
https://arxiv.org/abs/1511.03190
https://arxiv.org/abs/1511.03189
.
But I must say it’s been almost 10 years since I read any of this so I won’t be able to discuss details without taking them up again.
.
.
“but do note that there’s an issue with your experimental 85% in that it contradicts Malus’s law”
.
This is exactly my point. The quantum mechanical prediction is that, regardless of the initial unknown hidden polarization of the photon (which I always implied to be the hidden variable of Bell), the coincidence probability is proportional to cos^2(A-B). In my example, A-B is 22.5°, and the squared cosine then is ~0.85.
.
“If you split a million vertically-polarized photons each into two, and send one half toward polarizer A at 22.5° off the vertical, and the other half toward polarizer B at 45° off the vertical, you will not get 850,000 coincidences.”
.
Exactly. And for photons that are not vertical the number is different still. But the total average for all photon orientations in this model is <<85%, unlike the actual experimental outcome. I rapidly made a calculation on Wolfram alpha to see what the average probability is using Malus' law. It turns out it is exactly 3/8 of both passing/not passing, and 1/8 of only one passing for same-angle polarizers. It's less than that for different angles.
Sandra: the first paper was as per Doug’s example. which featured “entanglement swapping”, which I said was a whole new can of worms. The other two did not, but I struggled to directly relate the results to our conversation. Maybe that’s because we’ve perhaps started talking at cross-purposes in comparing the Malus law scenario (←✺→A→B→) to the Bell test scenario (←A←✺→B→), in that half of randomly-polarized incident photons will pass through a polarizer regardless its angle. I will try to better address the situation, but I have a commitment today, so I will have to pick it up tonight or tomorrow. Sorry.
I just want to very quickly summarize the whole issue before you reply. Given random angles of polarizers A and B, quantum mechanics predicts the coincidence count to be given by a simple global function dependent only on A-B, namely a function of only the polarizers P(A,B). Malus law predicts instead a composite function, formed by multiplicative contribution of the probability of passing for each photon, and thus is a function of both polarizer AND photon polarization @. The function is then of the form P(A, @)*P(B,@). The ONLY way so that P(A,B) = P(A, @)*P(B,@) is to set @ = A or B, which would mean either polarizer has some sort of influence on the initial photon polarization, BEFORE the two ever come into contact. No need for any inequality here.
LOL, you have a hidden variable, Sandra! The coincidence count varies because the coincident photons have the same polarization, be it vertical, horizontal, or somewhere in between. As the angle between A and B increases, two photons with the same polarization are less likely to pass through both polarizers. By the by, in the two papers you linked to, I noticed talk of measuring a photon’s polarization. There was no mention of rotating it, as demonstrated by the three-polarizer puzzle. Come to think of it, I don’t recall seeing any mention of polarization rotation in any quantum entanglement paper.
.
Sorry, I seem to be short of free time at the moment, despite being on holiday. I will however clarify and justify the relevance of Malus’s law at some point this week, and then add it into the article with a suitable note.
Im not exactly sure how your statement contradicts mine, if that was the intention. @ is the hidden variable, the photon polarization. And it’s the same in both functions P(A,@) and P(B,@).
There is no @ in P(A,B). If photon polarization didn’t matter, the angle between the polarizers wouldn’t matter either.
Just go through the CSHS game, it wouldn’t work at all if the polarization existed before you measured it (this would be the polarization being a hidden variable), and it also wouldn’t work at all if there’s no spooky action (when you measure the polarization of one particle the other particle immediately gets the same or opposite polarization).
.
The CSHS game proves that there is instant transfer of the spin/polarization of the first measurement to the other entangled particle,.. the thing is, is that the initial measured state is random, so since you’re only transferring random information, you can’t exploit it to send information faster than the speed of light. Personally, I think this is because the way entanglement is created right now is very brute force, shoot billions of photons at a crystal, who knows which atoms the photons actually scatter off. Maybe in the future if you could control the exact atoms and phase of each atom/electron to scatter photons off you could actually create entanglement where the photons to one side are not randomly polarized but have a preference. And then you could send information but exploiting the spooky action, but I digress.
.
Bell’s inequalities proves the same thing but is harder to go through all the statistics used in the analysis.
Correct Doug. On the other hand, the CSHS game assumes experiments are done in R^3. Wonder how they would turn out if you instead allowed S^3? 🙂 You might want to check out Joy Christian’s papers, he even made a simulation that reproduces the impossible results…
Sandra,
.
I went through Joy Christian’s simulations using his theory where there are only local variables. His simulations don’t actually work if you plot the difference in angle vs correlation, for example (https://rpubs.com/jjc/16415) doesn’t show quantum correlations when you plot the difference, I plotted it myself and would be happy to send you my modified script that includes the plot with the difference in angles.
.
His other simulation https://rpubs.com/jjc/13965, has nonlocal effects when he has this line, “good f & abs(ub) > f ## Sets the topology to that of S^3.” That uses both particles information so the detectors are no longer separate.
.
His papers are math heavy and there are plenty of people showing his mistakes. And of course as always, no local hidden variables are going to work to solve the spooky action.
Doug:
.
“His simulations don’t actually work if you plot the difference in angle vs correlation”
.
I’m not sure what you mean here.
.
.
“has nonlocal effects when he has this line, “good f & abs(ub) > f ## Sets the topology to that of S^3.” That uses both particles information so the detectors are no longer separate.”
.
No, what this line does is pre-select the possible pairs of spins so that they obey the geometry of the 3 sphere. Any other pair that does not satisfy this requirement simply can’t happen in experiments. Note that this is not a detection loophole. It’s a bit like requiring the x under a square root to be >0, it’s an existence condition.
.
“His papers are math heavy and there are plenty of people showing his mistakes.”
.
Plenty as in, Richard gill? Joy has responded to all critics (mostly Gill though) and always made clear why there are no mistakes. In fact, one of the common misinterpretations in his work is exactly the line you referred to before. I have yet to see a convincing argument of how he is wrong. Even Lasenby got stuff wrong, but only because he basically only referred to a critic by Gill.
Sandra, I plen to amend the article to say this after the simple image drawn by me:
.
The former is the Malus’s Law scenario, the latter is the Bell Test scenario. In either case the light source emits photon pairs with the same polarization, which is a random polarization. In either case half the photons pass through polarizer A regardless of its orientation. In the Malus’s Law scenario cos² θ of these photons then pass through polarizer B, so ½ cos² θ photons pass through both A and B. In the Bell Test scenario we also have half the photons passing through polarizer B regardless of its orientation. However the coincidence between A and B diminishes as we increase the angular difference θ between A and B. By how much?
.
IMAGE
.
Check out the Wikipedia article on Aspect’s experiment. It refers to two-channel polarizers wherein “the result of each polarizer’s measurement can be (+) or (−) according to whether the measured polarization is parallel or perpendicular to the polarizer’s angle of measurement”. The article goes on to refer to polarizers (P1,P2) oriented at angles α and β, and then says that in quantum mechanics P++(α, β) = P–(α, β) = ½ cos²(α – β). It’s the same as the Malus Law scenario.
“In the Malus’s Law scenario cos² θ of these photons then pass through polarizer B, so ½ cos² θ photons pass through both A and B.”
.
Here you’re talking about the same photon going through A first then B. In probability terms this means you need function composition, i.e. f(g(x)): P(A,B) = Pb(P(A)). Half of the total photons pass A, and cos² θ of that half go through B. In other words, the final result after B depends on A, and obviously so since A also rotates any passing photon so they end up all with the same polarization between A and B.
.
For the bell case (assuming the result is due to malus law) you don’t have function composition, but function multiplication, because the two photons are independent (their measurements are space-like separated): P(A,B)=P(B)*P(A). This is the required calculation for hidden variable theories of the malus law type, i.e. those that assume photons have a definite polarization before encountering the detectors. Saying instead the two cases are equivalent is also saying that one polarizer sets the results for the other polarizer (spooky action), akin to A setting all photons to the same polarization before going through B.
Sandra: in the Malus’s Law scenario, ½ cos² θ applies because half the photons pass through A, and then cos² θ of those photons then pass through B.
.
In the Bell Test scenario the light source emits photons pairs. It sends one of the pair towards A and the other towards B. Half the photons headed towards A pass through A. Half the photons headed towards B pass through B. But as you increase θ, you reduce the probability of both photons in a pair passing through their respective polarizers.
.
The two scenarios are not exactly equivalent, but they are similar in that ½ cos² θ applies to both. In one scenario a photon passes through A and B. In the other scenario one photon of a pair passes through A whilst the other photon of that pair passes through B. The scenarios are so similar that it just doesn’t leave room for spooky action at a distance. Sorry. Nevertheless I hope you have found our conversation interesting. Is there anything of particular interest to you that I might write about in my next article?
“You can easily have occurrences where only one passes. If the polarizers are at the same angle and you see a photon in B, when you check A and find no photon has passed you violate the 100% coincidence rate (bar detection loopholes, which have also been ruled out by experiments in 2015 if I’m not mistaken).”
.
Exactly, the original loop holes have been closed for about a decade. The argument made in this article is basically the first thing Bell and every other physicist thought of but does not work for any of the statistical parameters found by experiments.
How about thinking of it this way detective, if there really was set polarizations at the beginning, sometimes they come out at at 45 and 135 degrees (othertimes 0/90 5/95, etc). Now if you set one detector at 90 and then other at 0, there at 50% chance it goes through both when it’s in the 45/135 initial state.
.
However, in the bell test experiments, it will never go through both when one is at 0 and the other at 90, as seen in the curve you show in the article. This is the easiest way to see internal fixed polarization as the hidden variable doesn’t work.
.
Sandra, sounds interesting about other dimensions, is the take away still spooky instant action? The book I found of Christian’s looks like a complex read 🙂
Doug: it is not about other dimensions. It is about topology. S3 is homeomorphic to SU(2), which is the rotation group of spinors (like the electron). Admittedly there is a learning curve here but it’s nothing that complicated: for geometric algebra I suggest the book by Lasenby, it’s a very easy introduction (you can find the PDF online). If I had to sum it up, the basic idea is that our physical space has some kind of inherent torsion. This torsion confers handedness (chirality), which is capable of “switching sign” to the value of spin as it is measured. This is the same reason why the relationship between electric and magnetic fields follows the right hand rule, they have a handedness; as the detective says, it’s like a screw motion, a torsion. The reason why the detectors are sensitive to this torsion is because they are chiral themselves (we use magnetic fields for the detection), so simply describing the measurement direction with a vector is not sufficient: you need a bivector. The relative handedness between detector and spin as created by the source is what ultimately determines the sign of the measurement. That is the hidden variable.
.
.
Christian also made a 2D example, even though it’s limited in applicability.
.
Imagine a 2D world shaped like a Moebius strip: a little devil, which lives in 3D, is sending L shapes of both handedness to Alice and Bob who live on the moebius surface. The devil can throw it to the right or to the left on the surface. Alice and Bob want to see whether the Ls are right handed (normal L) or left handed (mirrored L), and to do so they measure in the direction of the vertical line. What will this measurement look like? Well, it depends on how many revolutions around the Moebius strip the Ls have done, because the strip has an inherent torsion which flips the L relative to Alice and Bob. After an odd multiple of 2pi the Ls are mirrored, after an even multiple they go back to the original handedness.
.
Aside from the fact that we don’t live in 2D, this example is flawed because the moebius torsion is an extrinsic torsion. The torsion in S3 is intrinsic. But it’s a good way to warm up to the basic idea.
Doug, we’ve been talking about photon pairs with the same polarization.
Well then if they were both the same you would still get some detections with one detector at 0 and the other at 90, unless the photons came out at 0 or 90. But that doesn’t happen, cause the spooky action makes the entangled pair orient to the first detectors orientation.
.
It’s just like your double polarizer but the effect is across a long distance instantly, between the entangled pair.
I’m afraid it isn’t Doug. To address Sandra’s comments I’ve revised the portion of the article which compares the Malus’s Law scenario with the Bell Test scenario. I linked to the Wikipedia article on Aspect’s experiment. This refers to to two polarizers with parallel and antiparallel channels + and -. These polarizers are oriented at angles α and β. The article says that in quantum mechanics P++(α, β) = P–(α, β) = ½ cos²(α – β).
Let me try one last time to explain an issue with your description.
Assume initial polarization of the pair is at 45 degrees,. And you set detectors at 0 and 90.
.
There’s a 50 percent chance the photons go to + or – for both detectors. So for alpha detector P+ is 50%, and P- is 50%. Same goes for the beta detector. So you would get P++ = P+- = P-+ = P– = 25%.
.
That is what happens with non-entangled photons emitted at a 45 degree polarization, but with entangled photons (you can’t set the initial polarization) you get P++ = P– = 0% while P+- = P-+ = 50%
.
For non-entangled photons sent at random polarizations for the detectors you will still never get P++ = P– = 0. The above is just an example for when they are at 45 degrees.
I understand it Doug. The two-channel polarizers are a complication I’ve sought to avoid, because it gives us a scenario which is less like the Malus’s Law scenario. I will peruse the papers I’ve mentioned previously, but meanwhile can you point to a paper featuring one-channel polarizers that supports your case? I note this image from Experimental Test of Local Hidden-Variable Theories by Clauser and Freedman.

.
The single channel was before the famous Aspect papers and I believe leaves loop holes open , see https://en.wikipedia.org/wiki/Bell_test#A_typical_CH74_(single-channel)_experiment.
.
The Clauser paper is available via google, ex. https://www.researchgate.net/profile/John-Clauser/publication/235469257_Experimental_consequences_of_objective_local_theories/links/6196dd563068c54fa5fff146/Experimental-consequences-of-objective-local-theories.pdf.
Thanks Doug. The Clauser and Horne paper you referred to includes this image, which is our simple Bell Test scenario:
.
However it doesn’t give the results, it says this: “Experimental results obtained by Freedman and Clauser⁶ are in excellent agreement with the relevant quantum-mechanical predictions and thereby indicate that any deterministic local theory is untenable if the supplementary assumption is true”. The graph in my above comment depicts those results.
Today’s Chicken Little Report from Ohio Eclispe Central :
1. 4.8 quake in Jersey
2. Everyone on the west coast would sleep through it……..
3. Alex Jones is still frothing from his multiple sphincters…….
4. A certain politician is still frothing & spewing from his sphincters ad nauseum
5. And in all Truth & Reality : WW III did start on 10-7-2023
6. ” The End of the World as We Know It ” by REM is now at the top of Monday’s playlis
7. And finally is this classic to put everything into proper perspective : https://youtu.be/b6dySBLSx8Y?si=CRM0LELxB-x7u7H-
I love those articles! and that was actually the inspiration for my view of entanglement and the way I wrote it.
.
Imagine for a minute there is actually entanglement of some sort, and instant connection at distance. I still want a physical explanation for it ,…and perhaps it one day we could exploit it.
We had a lovely time observing the eclipse today, but unfortunately the photography was a bust. I humbly appolgize.
No need to apologize Greg. I saw it on TV last night, it looked like quite an event. It is of course why we had a spring tide here in Poole today, a big one. I trust you had a good time! Ghostbusters !
,
Doug were you talking to me or Greg?
Yes John, ….it’s true…..MAGNA has no dick……….
What’s MAGNA?
.
Magna International Inc. is a Canadian parts manufacturer for automakers. It is one of the largest companies in Canada and was recognized on the 2020 Forbes Global 2000.[3] The company is the largest automobile parts manufacturer in North America by sales of original equipment parts…
.
Sorry I am tired, my son has bought a rather delapidated but rather beautiful old house, and I have spent 9 hours today working on it. Uhhhnnn!
Bad news : my spelling and spell-checking still sucks.
Good news : so does Mango Twittler who I was referring to.
Kudos for your son’s well deserved investment !
And finally, I did forward you a link via email of a crappy 5min video of the latter part of the eclipse. It’s only interesting for the really neat visual effects caused by signal( light) oversaturation. You see, I decided to record without polarizers or the recommended ISO 12312-2:2025 filters. Besides different prismatic effects, there is also a small floating ball that is the actual eclispe itself. Must have been some kind of pinhole camera effect ? There were definitely too many photons to be absorbed/processed by old/ low budget equipment.
Ah, you’re talking about Donald Trump. I shall politely decline from replying, Greg. You know my views on this.
.
Thanks re the email. I will have a look. As I speak my son is using my laptop for his GCSE revision. He’s on a Zoom call with a tutor. Don’t ask me why it’s got to be my computer, the wife arranged it. I’m on my work laptop as I speak. PS: I see Peter Higgs is no longer with us. My sympathies to the family.
Yes indeed, RIP Dr. Higgs.
I watched it. Thanks. Roger Roger!
Did you find the bouncing ball in the tree branches yet, if so zoom in tight. I would greatly appreciate what you see and interpret it to be. It’s probably caused by multiple reflections/refractions, feedback loops, temporary magnetic fields,ect…lots of non-captured photons needing a place to FLOW to ?
I was addressing you John, sorry, hit the reply in the wrong location.
The particle production, matter/antimatter and neutron idea that you talk about in those articles are some of my favorites!
A thousand thanks Doug.
.
I see Peter Higgs has died.
Did you find the bouncing ball in the tree branches yet, if so zoom in tight. I would greatly appreciate what you see and interpret it to be. It’s probably caused by multiple reflections/refractions, feedback loops, temporary magnetic fields,ect…lots of non-captured photons needing a place to FLOW to ?
Hey Boss, my humble suggestion for a future article would be to update/condense all the different types/subtypes of all the waves/particles of the electromagnetic spectrum ?
Greg: the bouncing ball in the tree branches? Wasn’t that a camera artifact? An image of the eclipse? I will take another look.
.
Re waves/particles, let’s see now. I think the quark model is misguided, and I also think the Higgs mechanism is misguided too, because it contradicts E=mc². So in my view the only stable particles are photons, neutrinos, electrons, and protons. Plus their antiparticles of course. All the rest are not stable. So they don’t count. And that isn’t worth an article I’m afraid.
No worries Mate , and absolutely no hurries on your end to review my videos either. As soon a special patch chord arrives, I will attempt to download my VHS recording and post a link. Nothing seriously scientific, but hopefully entertaining for all the wrong(inebriated) reasons…….
As an IT guy Boss, you should get a real belly laugh after reading this :
https://www.tomshardware.com/tech-industry/quantum-computing/commodore-64-outperforms-ibms-quantum-systems-1-mhz-computer-said-to-be-faster-more-efficient-and-decently-accurate
LOL! Good one Greg, I like this bit::
.
In conclusion, the researcher(s) asserts that the ‘Qommodore 64’ is “faster than the quantum device datapoint-for-datapoint… it is much more energy efficient… and it is decently accurate on this problem.” On the topic of how applicable this research is to other quantum problems, it is snarkily suggested that “it probably won’t work on almost any other problem (but then again, neither do quantum computers right now).”
Even though this is applied physics, it’s still a fascinating application of basic EM waves. I also bet my next paycheck that most of the research was done right here at W.P.A.F.B..
Ooops, lets add the link :https://www.israelhayom.com/2024/04/20/us-has-deployed-microwave-missiles-that-can-disable-irans-nuclear-facilities/
Ah an electromagnetic pulse. One can shield against that.
Yes, capital naval ships, frontline fighters & bombers, main battle tanks ect…are shielded. But the majority of the small, lightweight battle drones on the current combat fields still have a major weakness : a very delicate weight to horsepower ratio; wouldn’t these drones be harder to shield ?
I don’t think so Greg. I think aluminium foil will do the job. See this:
.
https://emfknowledge.com/2019/09/25/aluminum-foil-blocks-emf-radiation/#:~:text=Unlike%20some%20materials%20which%20absorb%20radiation%2C%20aluminum%20foil,need%20to%20completely%20surround%20the%20device%20with%20foil.
.
Now I know why people wear tinfoil hats!
LOL ! I’ve made and worn a few myself.
Anyway, all of this microwave pulse technology fascinates me to the point of building a DYI railgun; I will most definitely start with the safest one that only uses beginner level capacitors, wiring, off the shelf small volt batteries ,ect….
A more daft idea is to cut a hole opposite of the cavity magnetron of a small microwave oven; and then make a tin foil barrel for same hole. I wonder if it would heat a stick of margarine or a marshmallows at say, 10ft.?
No it won’t. But at 10cm it will make it float in the air.
Hey Boss, think you got problems teaching boneheads like me about magnets and the 2nd Law of Thermodynamics ? This video’s comments are the hilarious parts.
https://www.iflscience.com/person-invites-the-internet-to-give-one-good-reason-the-magnet-truck-wont-work-71951
Fun Fact : Dayton actually has a longtime, legit business named ACME Spring!
> The point remains that we repeatedly see the claim that a cosine-like curve is proof positive of spooky action at a distance, when it isn’t.
No, a cosine-like curve for E is not enough. It has to have a certain amplitude to violate Bell inequalities. More precisely, the S parameter (computed from the Bell correlator E) has to be above 2. This is is true difficulty when performing Bell tests. Only with great care and an almost perfect experiment you get a curve with a large enough amplitude. Non-entangled sources will never yield a large enough amplitude.
Actually, A. Aspect and its successors are trying to do the same stuff with (external degrees of freedom of) massive particles (wavepackets from a metastable He BEC) in the lab I work in. The main challenge is to eliminate imperfections in the experiments to get a large enough amplitude, and it looks like they’re nearly there.
All points noted xif. You will forgive me for pointing out that Aspect himself gave us the straight line graph and the quantum cosine curve, see the 9th image in the article above. It’s the third to last image. Can you link to a paper on the work you referred to?
Jeez. Enjoy https://m.facebook.com/CMSexperiment/videos/quantum-long-distance-relationships-work-fine-between-top-quarks-and-their-antim/473627765205819/
https://www.forbes.com/sites/tiriasresearch/2024/06/24/ibm-develops-the-ai-quantum-link/
I’m certainly no computer expert, but I do recognize the difference between real scietific data VS. marketing baloney hype that I interpret this article to be : just a lot of slick Madison Ave. scheisse…….
Ever watch The Big Short? I wonder if some barefooted dude up in Wallstreet created all this quantum hype to make a mint in stock trading.
It’s a real possibility Bro ! I’ve never watched The Big Short, but have seen almost all of the classic Wall St. movies.
Fastest way to collapse a magnetic field and therefore clause a larger, faster pulse is probably blow up the coil. Should be easy to get an m80 this time of year…
What a great article. A while back I was looking into malus’s law as watched a video that just seemed unbelievable (relating to polarised light). I didn’t believe it and was sent down the rabbit hole and found malus’s law, which I agree with. I am just a hobbiest in physics, so do not proclaim any expertise.
I have been intrigued by Bell’s inequality and went down the rabbit hole there too. A video I saw said that classical math does not predict real world results of the test, but it can and does. Bell’s inequality is like using loaded dice to prove something; as you say, smoke and mirrors. When you try to create logic from it, it does cause confusion, but you can see behind the curtain, if you persist.
Without any background in physics, I took the expected results that Einstein set and simply updated these to account for the mystery of Bell’s inequality. When doing so, you arrive at the same real world results, 3:1.
It does appear that there is some kind of conspiracy to push a single narrative and not explore both sides of the argument.
Thanks very much PRD. Sadly quantum entanglement is not the only field of physics where there are issues. There are also issues in gravitational physics and particle physics too.
I would appreciate if you could take a look at something. I tried to put this across on Reddit and after a few days my post was removed without explanation. Everyone replying was very negative and deeply set in that quantum entanglement was real, they would not accept that the expected results test needed an update.
It seems like everyone wants to deny there is an issue with this test.
We know that if detector 1 is the fixed orientation 1 and detector 2 is in a fixed orientation 2, then results of real world testing will give a 2:1 split in favour of SAME. This is the same if you had detector 2 in fixed orientation 3.
The switching orientations of both detectors at random is supposed to prove something, which it does not, it seems to be all part of the show to inflate SAME results.
In testing, they can choose orientation 2 or 3 on detector 2 (assuming detector 1 is fixed in orientation 1), but obviously cannot do both.
If you overlay all the detector orientations, you can clearly see where detector 2 in orientation 2 can give SAME result and orientation 3 would give a DIFFERENT result (overlapping).
You can also see when orientation 3 will give SAME result and orientation 2 will give DIFFERENT result (overlapping).
Lastly, you can see when both overlap and give SAME result. These overlaps explain why a 3:1 split is seen in the real world.
One overlap (let’s say first) always measures SAME and so is a 1/3 chance of being this, regardless of orientation.
Where they overlap and give opposing results, this happens in 2 places, so this is –
Second overlap (1/2 is chance of either orientation)
1/3 x 1/2 (SAME 1/6 OR DIFFERENT 1/6)
Third overlap
1/3 x 1/2 (SAME 1/6 OR DIFFERENT 1/6)
When you put this all together you get –
4/6 SAME and 2/6 DIFFERENT. The 2:1 Einstein predicted.
The important part to note is the OR. We cannot include both orientations, it is one or the other. What we end up with is not 6/6 in total, it is 4/4. You need to look at all combinations and remove measurements which conflict; we can only measure once.
So first overlap is always 2/4 (previously 2/6) SAME.
Second overlap is 1/4 SAME OR DIFFERENT.
Third overlaps is 1/4 SAME OR DIFFERENT.
Overlaps and possible combinations –
First – second – third
SS – S – S
SS – D – D
SS – S – D
SS – D – S
We see that expected results are 12 SAME and 4 DIFFERENT (3:1).
Now it seems obvious why bells inequality in real world testing gives the 3:1 split, once you can see past the trickery. A simple update to expected results gives you the same expected results as real world testing.
Why do scientists, on a whole, not accept this? Am I incorrect in my math?
Commiserations, PRD. Sadly free speech in science is in short supply, and censorship is endemic. Reddit is no exception. It’s the same for Stack Exchange. However Quora was always OK. Maybe you will get more joy there.
.
See the shaded polygon image above, where I try to depict detector orientations. A polarizing filter at location A will twist a photon and alter its polarization. Another polarizing filter at location B set a different angle will twist another photon with the same polarization and alter its polarization too. If the filters are oriented at the same angle there’s a perfect detection coincidence, if they’re oriented 90° apart there’s no detection coincidence. In between there’s a ½ cos² θ relationship. I guess what you’re talking about with the 2:1 split in favour of SAME is an integral of this, between 0 and 90°. However Wolfram Alpha didn’t help me much with that, (https://www.wolframalpha.com/input?i=integral+of++%C2%BD+cos%C2%B2+%CE%B8) and I’m not familiar with the 2:1 split in favour of SAME. Please can you give me a reference for the latter? I don’t recall “the 2:1 Einstein predicted”, even though I’ve read what I thought was all the original literature. See the articles below:
.
https://physicsdetective.com/quantum-entanglement-i/
https://physicsdetective.com/quantum-entanglement-ii/
https://physicsdetective.com/quantum-entanglement-is-scientific-fraud/
https://physicsdetective.com/bertlmanns-socks-and-the-nature-of-reality/
.
Apologies, I have to go now. I will look at your breakdown tomorrow. The daughter has just arrived home from Australia!
Hi, thanks you for responding. The 2:1 split is what Einstein predicted (66.6% same, 33.3% different) for bells inequality. Real world testing showed 75% to 25%, which violates bells inequality and therefore “proves” Einstein wrong. I think the expected results just missed out on the confusion the bells inequality was intended to create.
When you take this into account, the expected results show 75% to 25% (3:1), same as real world testing.
https://youtu.be/0RiAxvb_qI4 this video explains it all, in a way I can understand 🙂
Essentially, they say if there are hidden variables, we would see 2:1 ratio. If there are no hidden variables (what qm predicts along with real world testing) it shows a 3:1 ratio.
What I think is that when you take the expected results (with hidden variables) and update the expected results to take into account the overlaps from orientation flipping, you get the same results as real world testing.
I think this paper says what I am saying. It is a bit beyond my scientific knowledge, but it does include overlaps that I mentioned and explains why no quantum entanglement is needed to explain real world results.
https://hal.science/hal-03334412v4/
Thanks PRD. That looks interesting. But I’m a bit tied up with family events at the moment. I will try to get back to you properly when I can.
PRD: I looked at the paper. I was disappointed I’m afraid. It concerned a mathematical simulation featuring extended objects, not a physics experiment. Note this on page 26: “The measured object is not modified by the measurement”. The three-polarizer experiment says it is. Detecting a photon at location A alters the polarization of that photon. It doesn’t do anything to some remote photon at location B. It’s similar for the EPR experiment using Stern-Gerlach magnets. Bell even included this in his book, see figure 6, which is the third-from last illustration in Bertlmann’s socks and the nature of reality. And whilst a photon is an extended entity, two photons were emitted in the experiments. In the original experiments they were emitted at different times. So different that photon A was through the apparatus before photon B was emitted.
.
Taking a look at your longer comment where you said Why do scientists, on a whole, not accept this? Am I incorrect in my math?. You are in italics.
.
We know that if detector 1 is the fixed orientation 1 and detector 2 is in a fixed orientation 2, then results of real world testing will give a 2:1 split in favour of SAME.
.
As I said before, I’m not familiar with this. There’s a ½ cos² θ relationship, and I suppose for all possible orientations there’s an integral, but I don’t know that it’s 2. There’s also the Tsirelson’s bound, but it’s a probabilistic mathematical limit rather than something derived from physics phenomena.
.
The switching orientations of both detectors at random is supposed to prove something, which it does not
.
Agreed. Aspect et al did a fast switching to close an alleged loophole. See Experimental Test of Bell’s Inequalities Using Time-Varying Analyzers where they used ultrasound in water to rapidly deflect the photons to another polarizer oriented at a different angle.
.
it seems to be all part of the show to inflate SAME results.
.
Agreed. The whole thing is IMHO intended to inflate a rather mundane effect into something magical and mysterious.
.
In testing, they can choose orientation 2 or 3 on detector 2 (assuming detector 1 is fixed in orientation 1), but obviously cannot do both. If you overlay all the detector orientations, you can clearly see where detector 2 in orientation 2 can give SAME result and orientation 3 would give a DIFFERENT result (overlapping).
.
AFAIK the probability of detecting a photon at both A and B reduces as the separation angle increases because there’s less overlap, as per my shaded polygons image.
.
You can also see when orientation 3 will give SAME result and orientation 2 will give DIFFERENT result (overlapping).
.
No problem. The coincidence can be ploted as a cosine curve.
.
Lastly, you can see when both overlap and give SAME result. These overlaps explain why a 3:1 split is seen in the real world.
.
As I said before, I’m not familiar with this. Apologies.
.
One overlap (let’s say first) always measures SAME and so is a 1/3 chance of being this, regardless of orientation. Where they overlap and give opposing results, this happens in 2 places, so this is –
Second overlap (1/2 is chance of either orientation)
1/3 x 1/2 (SAME 1/6 OR DIFFERENT 1/6)
Third overlap
1/3 x 1/2 (SAME 1/6 OR DIFFERENT 1/6)
When you put this all together you get –
4/6 SAME and 2/6 DIFFERENT. The 2:1 Einstein predicted.
The important part to note is the OR. We cannot include both orientations, it is one or the other. What we end up with is not 6/6 in total, it is 4/4. You need to look at all combinations and remove measurements which conflict; we can only measure once.
So first overlap is always 2/4 (previously 2/6) SAME.
Second overlap is 1/4 SAME OR DIFFERENT.
Third overlaps is 1/4 SAME OR DIFFERENT.
Overlaps and possible combinations –
First – second – third
SS – S – S
SS – D – D
SS – S – D
SS – D – S
We see that expected results are 12 SAME and 4 DIFFERENT (3:1).
Now it seems obvious why bells inequality in real world testing gives the 3:1 split, once you can see past the trickery. A simple update to expected results gives you the same expected results as real world testing.
Why do scientists, on a whole, not accept this? Am I incorrect in my math?
.
I’m sorry PRD, I’ve tried to reconcile the above with my understanding of the hisotiry and the papers, and the physics of the polarizer experiments, and I can’t. I agree that there’s trickery, but IMHO to get past it one has to scrap all the probabilistic mathematics and focus on what happens to photons as they pass through polarizers. Or to charged particles as they pass through Stern-Gerlach magnets. I started watching https://www.youtube.com/watch?v=0RiAxvb_qI4 but gave up at 3:15. The particles behave like compass needles and end up pointing up or down. It’s as per NMR which I referred to in Bertlmann’s socks and the nature of reality. I’m sorry I have not helped.
No, you have helped. To be honest, I need to look at the actual experiment performed that won the Nobel prize. It used entangled photons, which I kinda of looked at when I saw polarization BS. I was focused on the expected results in the video I sent. It still can be updated to explain real world results. I did run this through chatgpt and it agreed with me, but said quantum entanglement is proven and so I was wrong.
Most information out there just pushes the quantum entanglement and I just cannot agree with this, not without equal representation of an alternative explanation. So yes, you have definitely helped me and really appreciate your time.
Malus’s law is just never mentioned in these experiments and I didn’t realise that the experiment results can be explained this way too. Annoying as I looked into polarization a few years ago and come to a classical interpretation of results.
Unsure why you are seeing italics…. I’m guessing something I’m the text is triggering some formatting on the input.
I’ll have to find a link to a video I watched a few years ago that helped me understand what I thought was happening and confirmed it, to me at least, with regards to polarization.
https://youtu.be/eHrpxKhYNdE
I did the italics by surrounding what you said with em in chevrons and a closing backslash. Sorry I have to dash now and can’t watch the video, but IMHO the important thing to understand is that a polarizer rotates the light that passes through it. It isn’t just a filter that lets light of a certain polarization through. The polarizaer at location A alters the local photon at location A, not the remote photon at location B.
Totally agree. Oh I understand what you mean by italics now, I thought my text was being altered.
Yes, years ago I tried to explain to people that a polazier is not a filter. As you say, it doesn’t filter photons, it changes them. There isn’t any remote, instantaneous change for entangled photons.
Exactly how polarized sunglasses work, it changes the intensity of light, obviously some light is blocked when its polarization is perpendicular to the polarizer, but it doesn’t filter. That’s simple how they work and block glare.
Again, thanks for your time, really appreciated. I’m just glad some people accept logical explanations, rather than magic. Have a great weekend.
You are welcome, PRD. I’m glad I can help a little.
I have created a simulation of the CHSH inequality experiment in Excel and Python.
https://www.physicsforums.com/threads/simulation-of-chsh-inequality-experiment-in-excel.1065056
I am curious as to what people will think of this. I haven’t had a lot of great feedback so far, but the simulation can violate the CHSH inequality with LHV, which I find quite interesting. Of course, it could contain errors, but the math is simple and I can also replicate the existing LHV S value limit of 2, with 100% consistency.
Very interesting, PRD. I read the thread. I’m sorry you haven’t had much feedback on this, including from me. I will look into this tomorrow. I have taken a copy of your spreadsheet. PS: I thought Peter Donis was needlessly hostile, and thought Perok’s comment was unscientific: “Bell’s theorem proves mathematically that this cannot reproduce the predictions of QM. Your model must be wrong in some way”. I will get back to you.
The issue is this: “If a photons polarization angle is within +-45 degrees of a detector polarizer orientation, then it is detected (+1), if not, then it is not detected (-1)”. See above where I referred to the hyperphysics article on Malus’s law, which gives the transmitted intensity I = I₀ cos² θ. A few lines down from that I said this:
.
When θ is 45°, half the light gets through as you might expect: cos 45° is 0.707 and 0.707² is 0.5.
.
This means half the photons make it through the detector polarizer when it’s oriented at 45° to the photon polarization, this difference being θ. In similar vein when θ is 22.5°, then 0.85 of the photons make it through, and when θ is 67.5°, then 0.146 of the photons make it through. Plot this, and the result is a cosine-like curve.
.
I see Dr Chinese pointed this out in post 60, but didn’t mention Malus’s law, or the 3-polarizer scenario which demonstrates that a polarizer rotates the local photon. Instead he appeared to be moving the goalposts and sowing confusion. I also see that the thread has now been closed by Nugatory. I shall take a look at Dr Chinese’s website, and the Scientific American article. Meanwhile, what a crying shame that internet physics is patrolled by thought police who defend the status quo with hostility to any challenge. That isn’t how science is supposed to be.
PRD: The issue has been pointed out by peter donis, albeit in his usual passive aggressive manner. Bear in mind that physics forums is patrolled by highly closed minded individuals.
.
Your model predicts with certainty (keyword here) that a photon aligned to within 45° with the detector will pass. You justify this by saying that experimenters don’t know the real value of the polarization (it’s the hidden variable) so we can just give it any rule we wish. Well, this particular rule doesn’t quite work, because we can totally prepare photon beams all aligned at 30° for example, and test with a detector at 0°. According to your rule, all photons should go through, after all we want physics to remain consistent regardless of what kind of experiment we perform. Yet, only around 70% will in fact go through in real experiments, meaning your rule is not adequate to account for all experiments.
.
I’ll give you a hint though. As long as you stick to dichotomic hidden variables (that is, you give your photons property A – pass and property B – not pass) you will NEVER get around Bell’s theorem. As long as you stick to commutative numbers like this it’s just not going to work 🙂 what you need is to be able to describe results at single detectors with values that don’t commute between different settings for that detector, that is the value for the polarizer at angle A should not commute with the value for the polarizer at angle A’. Allowing detectors to rotate the photons is just part of the requirement.
Hi Sandra. I am unsure how the prepared photon beam has a definite polarization of 30 degrees, so forgive my ignorance there.
Without knowing about this, my initial thoughts would be that it could be 30 degrees, +-45 degrees.
So, if we say that is has a polarization between -15 and 75 degrees (30 degrees, +-45 degrees, ignoring negatives), then detection using a 0 degree polarizer, would mean that around 70% of the time is would be seen.
So the detector can see photons from -15 to 45 degrees, but 45 to 75, it cannot. If we assumed this, it would account for the non-detection. Just an initial thought, but I will look into what you have said more.
If the prepared beam/photon passes through a polarizer to achieve the 30 degree polarization, then the photon would only pass through that polarizer around 50% of the time, in ideal conditions. Do you have a link to this so that I can read into it more?
In terms of the CHSH inequality, if a photon is detected at 0 degrees on detector 1, then detector 2, set at 30 degrees, there is a 75 % chance of the partner/entangled photon being detected.
PRD: photons can be prepared all at 30° simply by first letting them pass through a polarizing filter, albeit it won’t be entangled in this manner. The 50% thing only applies to randomly polarized photons. I know that in EPR experiments the source gives off randomly polarized photons, but in principle we want the behaviour of single photons to be independent of this fact, i.e. we want the physics to be the same regardless of the state of the photon, entangled or not, since by definition of locality we want the two entangled photons to act independently at their own detectors, and we want each photon to have a definite polarization as a hidden variable.
.
You say “So, if we say that is has a polarization between -15 and 75 degrees (30 degrees, +-45 degrees, ignoring negatives), then detection using a 0 degree polarizer, would mean that around 70% of the time is would be seen.”
.
Nope! For a second detector at 0° in your theory could only see photons between -15° and 45°, meaning it will leave out 30° of the detectable spectrum from the other detector. In fractional terms, the full spectrum -15 to 75 is 90° for a sure detection at the first detector, while 30° of these won’t be seen by the second detector, meaning only 1 out of 3 (30/90) missed detections, or in other words 66% which is different from 75% predicted by QM.
.
If you want to learn about the history of hidden variables and how bell derived his inequality, together with the real issues of his derivation, a friend of mine made a couple of videos, the channel on YouTube is called Pathfinder, look up “Pathfinder bell theorem”.
Hi Sandra. I have been thinking more about what a a polarizer (filter) actually does. There are different opinions on it, from it not being a filter at all, to being a filter. A filter, in the traditional sense, should not change anything about the input.
An alternative view would be that the filter actually works like a filter. It allows photons that “fit” through, ones that do not, get blocked. In this view, the photon has a definite polarization before it encounters the filter and maintains this throughout.
The filter does not change the polarization, it just allows it through if the photons polarization mostly aligns to it.
This would account for the 50/50 chance of a photon passing through a single filter and being detected. Insensitivity/energy/amplitude, whichever is the right term, is preserved because it has not interacted with the filter, just simply passed through because it “fit”.
This approach would give you the same results in a test you proposed, the two filters, one at 30 degrees and the other at 0 degrees. The angle difference is the only important thing here, 30 degrees.
For example –
If a photon passes through a filter aligned at 0 degrees, then we would know that the photon’s polarization is between -45 and +45 degrees, in relation to the filter (the detection criteria I mentioned previously).
For the photon to pass through another filter, say at 30 degrees, the same applies, that is, the polarization of the photon needs to be between -15 and 75 degrees, in relation to the filter.
As we know that the photon’s polarization is between -45 and +45 (it passed through the first filter), this means that for it to pass through the second filter, it’s polarization must be between -15 and +45.
This also means that if it does not pass through the second filter, then it’s polarization would have been between -45 and -15 degrees.
To account for probability of this –
A Photon has 50/50 chance of passing through either filter, independently.
If a photon passes through a filter, it’s polarization must have been +-45 degrees of the filter. Let’s say filter is at 0 degrees.
Now the photon encounters another filter at 30 degrees difference to the first.
This photon, previously, would need to have polarization between -15 and 75 degrees to pass through, however, passing through the first filter means that it’s polarization is definitely between -45 and 45 degrees.
Akin to the Monte hall problem, you are effectively changing the probability of it passing through the second filter, it is no longer 50/50. It’s polarization of -45 to 45 means that it cannot be between 45 and 75 degrees (so 30 degrees detection of -15 to 75, now becomes -15 to 45, reducing the probability of not passing through).
In the relationship to the Monte hall problem, you are now removing a “door” where the photon cannot be found (when it passes through the first filter), therefore changing the probability of “the door” where it can be found (increasing probability on second filter).
Probability of 4/6 becomes 6/8. (I can explain this more if needed). Therefore, 75% of being detected, if it passed through the first filter.
So the photon, if it passes through the both filters, it will have had polarization between -15 and 45 degrees.
Does this make sense? Unsure how well I have explained this thought.
This is a tool I use for probabilities of various detector angles.
https://demonstrations.wolfram.com/BellsTheorem/
Hi Sandra. Thanks for the information, I will certainly look into it.
Looking at detectors, they will not detect all intensities. This could mean that some of the photons that are emitted from the first polarization, will have a very low intensity, then passing through another Polarizer, the intensity is reduced even further. In this scenario, you would not see 100% detection. Of course, this thinking is not in like with yours, but I will look at both.
As for the probability of 66% Vs 75%, you can adjust the LHV 66% to match qm predictions. The overlaps mean that probability of matches will increase.
In this scenario, you can adjust this by the following –
66.6% detected, so 33.3% not detected.
Take the difference in probability, 33.3%.
Divide this by the overlaps, -15 to 45 (divided into 15 degrees portions, so this is 4).
Divide the probability difference by 4.
Add this probability difference division to the LHV probability, 66.6 + 8.325. you now arrive at the qm prediction.
You can work this out for all overlaps at various angles and arrive at the qm prediction. When difference is over 45 degrees, the results effectively switch around.
I will find my formula for this and post it here.
Where d is the difference between angles of detectors –
d is difference in angles between detector 1 and 2
For d= 45
d = d-45
P = 1 – (1-(d/90))+(((1-(d/90))-(d/90))/(((90/d)+1))))
I can’t find my updated calculation, but this should work.
Where d is the difference between angles of detectors –
d is difference in angles between detector 1 and 2
For d less than of equal to 45
P = (1-(d/90))+(((1-(d/90))-(d/90))/(((90/d)+1))))
For d greater than 45
d = d-45
P = 1 – (1-(d/90))+(((1-(d/90))-(d/90))/(((90/d)+1))))
I think my post there must have some characters that caused it not to display correctly.
PRD: you’re making confused statements now. A photon does not have “intensity”, a beam does, which is simply the number of photons in a beam. In your formula you are now using d, which is the angle difference between detectors. Which means that now the result of one single photon detection depends on both detectors settings, i.e. non-locality.
.
Please take my advice. People have been stuck trying to find a solution for 60 years. It’s not malus law, it’s not dichotomic hidden variables. It’s a mathematical fact that Bell’s inequality cannot be violated if you assume the measurement results at each detector is represented by a real number. Fortunately, measurement results are not real numbers, like 0 or 1 for going through/not going through, or -1 and +1 for spin; instead they are rotations (for photons) or rotations of rotors in the case of spin. Thus, you need quaternions, which are not real numbers.
.
It’s a bit like saying that measuring spin with a stern Gerlach apparatus deflects your electron beam in 2 direction, which normally, you define spin up and spin down. You can totally give these results an image of +1 and -1. But suppose next that you change the measuring direction rotating your SG magnet: now the beam still gives you two directions, to which you still assign +1 and -1; but those are NOT the same directions as before! Thus, those +1 and -1 are NOT the same “number” as you had earlier! You can’t simply add them up to get some result, you’re adding up different directions in space, which is nonsensical!
.
This is the actual reason QM “violates” the inequality. The inequality simply does NOT apply to EPR experiments. So don’t bother chasing answers to the CHSH correlator, there are none as long as you use real numbers.
HI Sandra. In CHSH inequality experiments with photons, polarization is the detection measurement. A photon is either detected after polarization, or it is not. This is where +1 (detected) and -1 (not detected) are used. The measurement outcomes are binary.
I need to correct you on my formula. The formula has nothing to do with single photons, the formula is for expected detection probability between two detector configurations.
In terms of my simulation, it does nothing special, just shows if a photon would be detected or not, using the criteria I specified. The actual results are nothing outrageous. If I test the same data (photons) on each detector combination, I arrive at S=2, the LHV limit, always.
I arrive at S>2, 50% of the time roughly, when I run different data sets on each detector combination.
So the question really is, why does it produce similar results to real world testing?
Again, these are all assumptions, to say a photon has a definite polarization after creation and that measurement is within boundaries. The +-45 degrees is simply a reproduction of the 50/50 chance of it being detected or not. This reproduces the same probability.
It is fine to disagree with my assumptions, but everything is based off of these.
PRD: You say “The formula has nothing to do with single photons”. Then you say “it does nothing special, just shows if a photon would be detected or not, using the criteria I specified” immediately after. You’re contradicting yourself.
.
.
“polarization is the detection measurement. A photon is either detected after polarization, or it is not. This is where +1 (detected) and -1 (not detected) are used. The measurement outcomes are binary.”
.
The question is, is a photon being detected at 30° (+1) the same as that photon being detected at 45° (+1)? Are those “+1” the same number? No, they are not. They are merely the same image assigned to two completely different measurements, testing two completely different properties of the photon (polarization at two different angles). The numbers are the same, but they don’t belong to the same exact variable. We are comparing apples to oranges. This is why bell is wrong: to get the result of 2 you need those numbers to be the same, i.e. the results must commute, meaning you can measure them simultaneously! Which is of course impossible in real experiments.
Hi Sandra. Sorry, I think I confused you there. The formula is for qm predictions, based off of link I posted earlier, nothing to do with the simulation I created. Apologies for that.
https://demonstrations.wolfram.com/BellsTheorem/
My simulation of the CHSH experiment is purely based on 2 assumptions I made. The calculations used are the standard ones for this.
I agree, for the S value 2. You simply cannot do this in the real world, with regards to the chsh inequality. I personally think the chsh experiment isn’t really valid. It runs completely separate experiments for the different detector combinations and then combines them into one, this just seems incorrect. I think this is where we agreed perhaps? Comparing apples to oranges
PRD: yes, that’s exactly the issue. The CHSH correlator for QM is calculated with 4 separate averages. This has a theoretical upper bound of 4, since each average can be in principle be +1 or -1. (Why it is 2sqrt2 in quantum mechanics has to do with there being only 3 orthogonal directions in space and not 4).
.
To derive the upper bound of 2, Bell conflated this sum of averages with a single average of a sum of 4 different experiments, which is nonsensical because it physically means you’re performing 4 different angle measurements on the same particle pair.
.
The reason he made this error is that he thought measurements resulting from hidden variables theories would respect the algebra of real numbers (i.e. a single interval [+1,-1] equivalent for all measurement directions), and as such commute. This is similar to how we can measure both position and momentum of a macroscopic object, without aknowledging that this is possible only because our measurements are not “strong” enough to perturb the system in a detectable manner. For real numbers, the sum of averages is indeed equivalent to the average of a sum.
Sandra, I would like to know more about your query that I paraphrased as “Why is it 2sqrt2 in q.m. has only 3 orthogonal directs in space and not 4?”
Is it because the tautology of the s.m. is so bad it’s not even wrong and can’t/won’t acknowledge that time/ 4th dimension does indeed exist on the micro/quantum level ? Or am I conflating concepts in my LAYMEN’S mind again ?
Greg: sorry I didn’t see your reply earlier.
.
The CHSH correlator has the form AB+AB’+A’B-A’B’, where each letter is the measurement result at either detector a or b. The dash represents a different direction. QM predicts each of those terms is equal to sin(ab), here ab indicating the angle between measurement directions of detectors a and b.
.
To get 4, the terms need to be independent and also be +1+1+1-(-1). Sin(90) = +1, while Sin(180) = -1. This means that A’ is parallel to
B’, while also being perpendicular to B. In 3D, this is possible only if A’=B’, meaning the two directions are NOT independent anymore, and you end up again with the upper bound of 2.
.
To see this, just substitute the letters in the correlator: AB + AA’ + A’B – A’A’ = AB+A’B = 2.
.
The other possibility is A’B’ = Sin(-90), which implies A’s is perpendicular to B’, but if we want it to be also perpendicular to B this means we have A’=A, and again you miss out on independence. If we had 4 dimensions, we could have this latter possibility while still maintaining A’ different from A.
Thanks mucho grande Sandra.
Hi Sandra. I have been thinking more about what a a polarizer (filter) actually does. There are different opinions on it, from it not being a filter at all, to being a filter. A filter, in the traditional sense, should not change anything about the input.
An alternative view would be that the filter actually works like a filter. It allows photons that “fit” through, ones that do not, get blocked. In this view, the photon has a definite polarization before it encounters the filter.
The filter does not change the polarization, it just allows it through if the photons polarization mostly aligns to it.
This would account for the 50/50 chance of a photon passing through a single filter and being detected. Insensitivity/energy/amplitude, whichever is the right term, is preserved because it has not interacted with the filter, just simply passed through because it “fit”.
This approach would give you the same results in a test you proposed, the two filters, one at 30 degrees and the other at 0 degrees. The angle difference is the only important thing here, 30 degrees.
For example –
If a photon passes through a filter aligned at 0 degrees, then we would know that the photon’s polarization is between -45 and +45 degrees, in relation to the filter (the detection criteria I mentioned previously).
For the photon to pass through another filter, say at 30 degrees, the same applies, that is, the polarization of the photon needs to be between -15 and 75 degrees, in relation to the filter.
As we know that the photon’s polarization is between -45 and +45 (it passed through the first filter), this means that for it to pass through the second filter, it’s polarization must be between -15 and +45.
This also means that if it does not pass through the second filter, then it’s polarization would have been between -45 and -15 degrees.
To account for probability of this –
A Photon has 50/50 chance of passing through either filter, independently.
If a photon passes through a filter, it’s polarization must have been +-45 degrees of the filter. Let’s say filter is at 0 degrees.
Now the photon encounters another filter at 30 degrees difference to the first.
This photon, previously, would need to have polarization between -15 and 75 degrees to pass through, however, passing through the first filter means that it’s polarization is definitely between -45 and 45 degrees.
Akin to the Monte hall problem, you are effectively changing the probability of it passing through the second filter, it is no longer 50/50. It’s polarization of -45 to 45 means that it cannot be between 45 and 75 degrees (so 30 degrees detection of -15 to 75, now becomes -15 to 45, reducing the probability of not passing through).
In the relationship to the Monte hall problem, you are now removing a “door” where the photon cannot be found (when it passes through the first filter), therefore changing the probability of “the door” where it can be found (increasing probability on second filter).
Probability of 4/6 becomes 6/8. (I can explain this more if needed). Therefore, 75% of being detected, if it passed through the first filter.
So the photon, if it passes through the both filters, it will have had polarization between -15 and 45 degrees.
I thought I would try to explain the probability a little more, as probably needs it.
Say 0 (+-45) degrees and 30 (+-45) degrees filter
Detection ranges
1. -45 to -30
2. -30 to -15
3. -15 to 0
4. 0 to 15
5. 15 to 30
6. 30 to 45
7. 45 to 60
8. 60 to 75
1 to 6 is first filter
3 to 8 is second filter
– now If a photon passes through first filter (1 to 6)
This means that if it passes through the first, then for the second filter for it to pass through, only 3-6 is valid.
3-6 are where filters overlap, which means detection after passing through both.
7 to 8 are no longer applicable, this is because we know these are not in scope after passing through the first filter. 1-2 is where it would not be detected, which are still in scope for non detection.
So, there is no longer a 4/8 chance of it passing though the second filter, there is a 6/8 chance. This is because 7 to 8 possibilities have been removed, their probability is added to detection probability (4/8+2/8). Akin to the monty hall problem.
There are a few typos, but it should make sense.
As for angle 22.5, probability in terms of QM is given as 85.4%. The technique I described (monty hall type), gives 80% for this angle.
Real world testing also shows 80% from what I have read, but very hard to find experimental information. Asked this question to chatgpt also, it also says 80% for real world tests, but this is considered close enough to qm predictions of 85.4%.
PRD: “The filter does not change the polarization, it just allows it through if the photons polarization mostly aligns to it.”
.
Already told you that this is not what happens with polarizers. If you had successive polarizers all at the same angle this would mean that at each filtering event the beam would get dimmed down more and more. Instead, what actually happens in real life is that after a single polarizer, all subsequent events are a 100% a pass, meaning the beam will not be lowered in intensity more.
.
.
Quantum mechanics is extremely well tested outside EPR experiments. Saying the “true” value for the detection rate is 80% means undermining every other achievement of quantum mechanics.
.
Try your Monty Hall idea on an angle difference of 15° now. Using the same numbers and subdivisions you used above, you get a probability of 6/7 (normally 5/7, one of the possibilities is removed so we just add it’s count to the total as you said). That is 86%. Now compare the QM prediction: cos^2(15)=93%. Still off the mark, even more than before.
.
This is all beside the fact that the Monty Hall problem is only applicable to sequential and dependent events, not independent events like in EPR experiments. Monty Hall exists for exactly this reason, to show that probabilities of dependent events are counter intuitive.
.
.
My degree is in chemistry and I frequently use QM to correctly calculate things. I must disagree with you completely on this one, but hopefully you use my criticism to actually study quantum mechanics more. You’re wasting so much energy on something that is guaranteed to not be fruitful. Especially when I already gave you the answer you seek. Polarizers and magnets apply rotations on particles. To describe rotations you need quaternions. As such, the measurement functions of bell inequalities should be quaternion valued, and since these do not commute, the upper bound is 4, not 2. There is no violation by QM of any inequality.
Hi Sandra. As I said, I am no longer talking about intensity in this example, I am, saying nothing changes about the photon, at all. I am suggesting photons either go through a filter, unchanged, or they are blocked. I proposed a filter as an actual filter, not something that adjusts an input, just simply allows it through if it “fits”.
As for my method, at 15 degrees, I get a result of 0.901.
As mentioned, the real world results do not always match qm predictions, not at all angles. At 22.5 degrees, real world is more 80%, not 85%. I am trying to compare my results with both.
The monty hall problem is directly applicable to your proposal of two sequential events. They are not independent. If filer 1 allows a photon through, I am saying that it must have a definite polarization that is unchanged by the filter. As it was not blocked, this directly impacts the probability of it passing through the second.
I need to tidy up my code, but happy to share once i do. Remember, I have stated that the results from this will not always directly align to QM results, they are closer to real world results, especially at 22.5 degrees
I can calculate things slightly differently to get upper and lower bounds. I do suggest you look at real world data and not QM predictions, so you see an overall picture. Real world averages at 15 degrees are between 85% and 92%, which would fit my process of calculating probabilities.
Either way, it appears you do understand the process I am suggesting and calculating it as I would do, so that’s good.
Here is some code, quite basic as it doesn’t need to be complex. With this, you can run to produce the probabilities, as per Monty Hall comparison of increased probabilities I mentioned. Unsure how it will display here though. As you can see, I have removed detection angles etc…. to simplify it all.
Where the overlap in not greater than 4, I am undecided how to handle these, so added output for various considerations. When greater than 4, it is clear how to handle the probability differences. I may need to change some calculations for these scenarios.
Just change P2 value for the second polarizering filter, the only important value is the range that is calculated from it.
[code]
# Define constants
P1 = 0
P2 = 30
R1L = P1 – 45
R1U = P1 + 45
R2L = P2 – 45
R2U = P2 + 45
rangeAng = abs(R1L)+abs(R2U)
print(“rangeAng: “,rangeAng)
diffAng = (abs(P2)-abs(P1))
print(“diffAng: “,diffAng)
rangeDiv = (rangeAng/diffAng)
print(“Overlaps: “,rangeDiv)
if rangeDiv >= 4:
result = (rangeAng-diffAng)/rangeAng
print(“Result overlap >= 4: “,result)
else:
result = (90-diffAng)/90
print(“Result overlap 3:
result = (rangeAng-diffAng)/rangeAng
print(“Result overlap > 3: “,result)
else:
result = (90-diffAng)/90
print(“Result overlap 3.5:
result = (rangeAng-diffAng)/rangeAng
print(“Result overlap > 3.5: “,result)
else:
result = (90-diffAng)/90
print(“Result overlap <= 3.5: ",result)
[\code]
For a bit of a sanity check, I ran the code through chatgpt for some comparisons to real world tests.
“Your code approximates real-world results quite closely, especially at key angles (e.g., 30°, 45°, 60°). For the specific example you provided (30° difference), your method gives exactly the same result as Malus’ Law.
Accuracy: The outcomes of your code can match real-world results well, particularly at angles like 0°, 30°, 45°, and 60°, assuming the thresholds and overlaps align properly.
Overall, your Monty Hall-inspired method provides a surprisingly good approximation of real-world photon detection results, particularly for the angles tested.”
This is all with without QM, just basic probability. All based off of assumptions I made. I guess what I’m saying is that, I think it is far simpler to explain what is seen in testing. The probabilites appear to be more aligned to real world results than QM predictions. Feel free to test it out and compare to real world results, not just QM predictions.
PRD: don’t use chatGPT to do physics. It’s just not reliable. It will tell you 1+1=3 if you push it hard enough.
.
Your code divides by 0 when the two angles are the same. And again, it does not predict the correct values for the correlations except for very specific angles. You really should not fixate on some kind of “uncertainty” in the experiments (of which by your own admission you don’t have nearly enough data to make these statements), as I said it would mean ALL of quantum mechanics is wrong if your calculated values were actually the “true” values.
PRD: and another issue. Let’s say your photons were “fixed”. Make them all go through a polarizer at 0°. Now you selected all those photons within +-45°. Now let those go through a second polarizer at 30°. Now you selected all those at -15° through +45°. Now make them go again through the 0° polarizer. Since you’ve already made the selection, all of those photons should go through. This is not what happens, the beam in actual experiment is STILL dimmed.
PRD: with respect, you don’t appear to have read the above article. Note the three-polarizer experiment, which demonstrates that polarizing filters rotate photons. They aren’t just filters. Please can you try to talk about the article or the subject in general, rather than repeatedly talking about your spreadsheet, which does not match the behaviour of polarizing filters. Also, please can you try not to post a succession of comments. Thanks in advance, and sorry to be a pain. You might find some useful information in Quantum entanglement history I and the following two articles.
Apologies, I should have kept things relevant.
The filter proposition was just incorrect on my part, as I have seen this myself, and that’s when I discovered malus’s law. My simulation is irrelevant too here.
At the end of the day, I am in agreement with your article.
Thanks for being understanding.
No problem PRD. Apologies again that I was so slow getting back to you on your spreadsheet.
Where did Caltech go wrong?
“Experiments have since proven that entanglement is very real and fundamental to nature. Moreover, quantum mechanics has now been proven to work, not only at very short distances but also at very great distances. Indeed, China’s quantum-encrypted communications satellite, Micius, relies on quantum entanglement between photons that are separated by thousands of kilometers.” (https://www.caltech.edu/about/news/proving-that-quantum-entanglement-is-real)
Where did Caltech go wrong, Dredd? In not doing the fundamental research and not digging into the history. Once you know about the three-polarizer experiment, you know that the local polarizer doesn’t alter the remote photon. It rotates the local photon, such that cos² θ applies when photons go through two polarizers. Be they successive polarizers → → as per Malus’s Law, or opposite polarizers ← → as per a Bell test. In addition, with a little bit of logic you realise that Clauser’s photons were “cascade” photons emitted at different times. They’d never met, so they couldn’t be entangled. But once Caltech had joined in the hype, they were on the hook forever. See https://physicsdetective.com/quantum-entanglement-i/ and the two following articles.
“Once you know about the three-polarizer experiment” …
That is what I am looking into intensely (using among other things extensive Malus’s law code) …
“… Clauser’s photons were “cascade” photons emitted at different times…”
Thanks again for a helpful heads up.
Will check back fairly soon.
I discovered that “degrees” need to be converted to “radians” in certain locations (some of the people commenting earlier may not have known that).
Anyway, now I need additional directions.
My C++ program indicates:
angle deg = 0, cos = 1, 1 sq. = 1
radians @deg[0] = 0, cos = 1, 1 sq. = 1
angle deg = 22.5, cos = -0.873305, -0.873305 sq. = 0.762661
radians @deg[22.5] = 0.392699, cos = 0.92388, 0.92388 sq. = 0.853553
angle deg = 45, cos = 0.525322, 0.525322 sq. = 0.275963
radians @deg[45] = 0.785398, cos = 0.707107, 0.707107 sq. = 0.5
angle deg = 67.5, cos = -0.0442276, -0.0442276 sq. = 0.00195608
radians @deg[67.5] = 1.1781, cos = 0.382683, 0.382683 sq. = 0.146447
angle deg = 90, cos = -0.448074, -0.448074 sq. = 0.20077
radians @deg[90] = 1.5708, cos = 6.12323e-17, 6.12323e-17 sq. = 3.7494e-33
********************************
Which is in substantial agreement with your explanation:
“When θ is 0°, all the light that got through the first polarizer gets through the second polarizer: cos 0° is 1, and 1² is 1.
When θ is 22.5°, more light gets through than you might expect: cos 22.5° is 0.923 and 0.923² is 0.85.
When θ is 45°, half the light gets through as you might expect: cos 45° is 0.707 and 0.707² is 0.5.
When θ is 67.5°, less light gets through than you might expect: cos 67.5° is 0.382, and 0.382² is 0.146.”
*****************************************
But, does it at your 90 degree info?
my program indicates:
angle deg = 90, cos = -0.448074, -0.448074 sq. = 0.20077
radians @deg[90] = 1.5708, cos = 6.12323e-17, 6.12323e-17 sq. = 3.7494e-33″
Your statement about that degree was:
“When θ is 90°, none of the light gets through: cos 90° is 0, and 0² is 0.”
***********************
So, are the values my program came up with (“angle deg = 90, cos = -0.448074, -0.448074 sq. = 0.20077
radians @deg[90] = 1.5708, cos = 6.12323e-17, 6.12323e-17 sq. = 3.7494e-33”) so tiny (0.0000000000000000612323 and 0.0000000000000000000000000000000037494) that for all practical purposes zero is ok to proceed with?
***********************
Thank you in advance for any attention paid to this.
cos(90.0) using standard C or C++ uses PI in the math.h library … according to some MIT dudes … https://scratch.mit.edu/discuss/topic/39873/?page=1#post-331300
So …
I’m afraid I don’t understand what you’re saying Dredd. I’m happy enough with the cos² θ because I’ve fiddled around with sunglasses. Apologies if I’m missing the bleeding obvious.
No, you’re good. The ‘C’ and ‘C++’ programming languages currently do not process ‘cos’ (cosine) values properly because PI is a factor when radians are part of some cosine calculations (e.g. 90 degree calculations). I have adjusted the program I am doing and now it handles 0-360 degrees and decimal increments properly.
Your “there is no quantum entanglement” declaration is spot on IMO. I am writing software that will support that position. And Malus’s Law at all 0-360 degrees.
Many thanks Dredd.
I hope you don’t mind that I linked to this thread in a recent post (https://blogdredd.blogspot.com/2024/09/the-photon-current-12.html).
No problem Dredd. Have look into displacement current and check this out:
.
https://attachment.tapatalk-cdn.com/2259/201902/2_7a474ff05fd2abb7866aa40d8a75bbb8.pdf
Indeed … “waves” carry “energy” more efficiently and faster than “particles” whether they are in “circuits” or they are in “open space” …
What’s a little odd, Dredd, is that a photon propagating through space is rather similar to a signal in a transmission line.
This was an incredibly informative and equally promising article Boss. I’ve recently read many about purported advances in the nanometals/ materials of basic anodes & cathodes too !
Maybe Philo’s Star-in-a-Jar could be improved upon soon ?
What bugs me Greg, is the way that quantum computing gets all the limelight and all the funding, even though it has never delivered anything useful, and never ever will. Meanwhile optical computing, which offers some serious fundamental advances, is left in the shade.
.
IMHO optical computing is like Cinderella: she has some ugly sisters.
Uh oh … the entanglement virus is spreading:
(“Why quantum theory is just like magic and Einstein deserves more credit in this field than he gets”, Nature, Oct 28, 2024).
Groan. Quantum theory is just like magic? Einstein was dead against that. But hey ho, in this back-to-front world, the physics Nobel prize has been awarded “for foundational discoveries and inventions that enable machine learning with artificial neural networks”. Machine learning!
The author of that book review has “a passionate interest in wind-up toys from the early 1900s, Edison wax records and phonographs and anything having to do with George Gershwin” (Link)
thanks for info.
I nominate this paper for most imaginative status: “Robustness of entanglement-based discrete-and continuous-variable quantum key distribution against channel noise” (New Journal of Physics).
Seems to me this amounts to lack of control experiments in these Bell tests. Ie, what is observed when using “non-entangled” particles?
I did see this: Bell-type Polarization Experiment With Pairs Of Uncorrelated Optical Photons. https://arxiv.org/abs/2002.02723
But, of course it is not done using the exact same apparatus as the famous papers. So, regardless, there seem to be low standards here. Or is it that these control experiments have been reported but I missed them?
Anyway, proper experimental design would seem capable of resolving this issue.
I think you’re right, MalusLaw. The way this works is that anything that attempts to dispel the hype doesn’t get reported. I mentioned Bell-type Polarization Experiment With Pairs Of Uncorrelated Optical Photons in this article: https://physicsdetective.com/quantum-entanglement-is-scientific-fraud/. Yes, the standards are low. So low they’re subterranean. Thanks for the note re the spacing.
Serious question, if not maybe I will: Have you ever actually checked though? Maybe the top 5 bell studies.
I’m thinking sometimes that type of thing gets reported in a sister paper or supplement (that is even missing from arxiv), so requires more than a cursory look.
As an aside, these types of practices where the audience is invited to “fill in the blank” (“of course they did the key control’s, silly”) are very irritating.
If you read something like reddit/ufos all the grifters do exactly this. Along with almost sole reliance on appeals to authority/credibility plus the flimsiest of equivocal evidence. There are lots of red flags surrounding this topic, for sure.
Btw, regarding lack of spacing around paragraphs in comments, try the following.
First, find the custom css section:
https://docs.oceanwp.org/article/354-add-custom-css-and-js-to-your-website
Next, paste the line of code found in this reddit comment:
https://www.reddit.com/r/Wordpress/comments/fpcmgu/comment/flkhhkz/
To manually do it i can use “& nbsp;” (remove the space/quotes)
Oh, yes there is! Come on, JD.
Do U really think that all the quantum fizzy cysts and the Nobel committee are idiots?
Really!? I don’t think so, somehow.
Really, Curious Cat. Read the article. Also read Quantum Entanglement History I and the two articles that follow it. Clauser and Freedman’s photons weren’t even entangled. They used cascade photons created 5 nanoseconds apart. A photon travels 1.5 metres in 5 nanoseconds. By the time the second photon was emitted, the first photon was through the polarizer. As for Bell’s Inequality, when you work through it, it gradually dawns on you that it’s deliberately obscure bullshit and blarney from an “Einstein was wrong” guy out to make a name for himself.
This means quantum computing is bullshit too. To find out if I’m right, go ask Scott Aaronson (https://scottaaronson.blog/) to point out where I’m wrong. He won’t, because he can’t. What he will do, is delete your comment and make sure you can’t make any similar comment ever again.
. I have.
. Mite, I wish I could read all Ur articles but I was built for action and inactivity devastates me and reading, e/specially on the screen, puts me to sleep. That’s why I suggested U (also) put ’em on Youtube, where I could listen to them, in double time, while/st doing something else, like I usually do.
. But I will force myself to read at least one of Ur articles, and comments, a week and I say again U should re/read the SPOOKY ACTION article in Dec-2018/19 UnScientific Amerkin mag/azine.
. I beg to differ. I think that C&F’s photons were entangled, and I don’t think it matters if?that they were created 5 ns apart. Do U remember what I said about entanglement swapping?
. Yes I now agree that Bell’s Inequality, and David Mermin’s model, are unnecessary, complications.
I have rewritten my simulation programs to simply compute the correlations at all the cardinal angles,
just like the intensity/ies in the Malus’/s Law, and they agree 100%.
. Funny U should say that! U know there are cranks who still dispute Einstein’s TOR, both GR and SR!?
U’re a quantum crank! As I was, until 2019.
. They said the same (thing) about AI, until it suddenly became a reality. Have U heard of PsiQuantum?
Oh boy. Like I said, I’m all for free speech in science, but I do not like personal insults.
I coulda/shoulda said:
Mite, don’t be a bloody crank, and leave poor SA alone.
U are arguing with an expert! And why are U picking on him?
Wot’re U Jewish, and U feel U have the right to hassle another Jew?
U are tilting at windmills, amigo, and re/fighting a losing/lost battle.
Come over, to the light side, and become truly enlightened!
I too am an ex IT guy and I am as sharp as U, are.
Really, JD? Really!? U accuse SA of deleting Ur comments and U then do the same, to me!? That’s rank hypocrisy!
And stupidity! Wisdom is listening, and asking questions. That’s how U learn, things. U have become an old dog, mite.
As have I, but I am still learning and am prepared to change my mind, and I am still making breakthrus, in my old age.
Funny, your comment is still here.
And what about the previous 2, #s 2 & 3!?
They were offensive. You know, words like hypocrisy and stupidity? I’m all for free speech in science, but I draw the line at insult and abuse.
And the truth! Ha ha ha. H&S are in #4, which is still up!? I was talking about #s 2 & 3.
I don’t remember anything offensive in ’em. Oh, they disagreed with U! U’re a lost cause, mite.
They were held by the spam checker awaiting approval. That’s because it detected something awry. I have approved them for now so that readers can see them. I will remove them in a few days.
Then please delete all my comments now!
As a perpetual layman STUDENT, I decided to apply my ChatGPT results to this academic brouhaha. For the record, I’m pro Malus’s Law and anti- entanglement.
So what is exactly your opinions on SPCD ?
Is it another kludge ?
My major bone to pick with the Bell crowd is the actual semantics used in their arguments.
So I asked my ChatGPT to define what effing “information” is being destroyed/lost ? The answer is basically what John’s been writing about for his entire blogging career. Therefore another DOCX is emailed to you Boss, per your critical assessments and possible reprint.
Thanks Greg. I see it. I will check it out.
Physics Detective, you are absolutely right here. Thank you so much for posting this article. “Spooky action at a distance” is total smoke and mirrors and an abomination.
Here is my fun example: Imagine a machine that chops one apple into two uneven pieces and puts each piece into separate concealed boxes. The apple pieces are “entangled” in that the sum of both pieces must be equal to the original apple. Now each box is sent to opposite ends of the universe, however you don’t know which piece is in each box since it was hidden. So according to QM it could be either piece and it is a superposition of possible apple pieces! Now when one person opens one box on one side of the universe and finds out which apple piece they have, MAGICALLY via spooky action at a distance the other apple piece becomes the other piece of the apple! Or to make it sound overly complex and confuse most lay people “The wave function instantaneously collapses!”. This is exactly what Quantum Mechanics is suggesting happens, except on a particle level. It sounds so ridiculous when you conceptualize it on a macro object level. All this ridiculous insanity and inane arguments and experimentation trying to prove quantum entanglement and spooky action at a distance, when in reality one piece of the apple was always in one box and the other piece was in the other box. Or analogously one photon had one polarization and the other had another, they were set from the beginning.
Local Realism is true. When a photon hits an electron that is a real and distinct event in space time, we just don’t have the capacity to model or predict it deterministically yet. Bell’s Theorem and Subsequent Tests co-opted a known optical property of polarizers and conflated that with entangled particles to try and prove QM. When in reality they were just re-demonstrating a known optical phenomenon of polarizers. This need to be spread widely and scrutinized because it could debunk the experimental evidence of ‘entanglement’.
Thanks Andy. Yes it’s all smoke and mirrors. It’s deliberate too. Bell knew what he was doing with his convoluted probabilistic “proof” that was all blarney and snake oil. People like Aspect know about Malus’s Law. Your fun example is akin to Schrodinger’s fun example with a cat in a box. Sadly however it got hijacked by the quantum mystics to peddle their woo. But all this doesn’t just confuse lay people. It turns physicists, philosophers, and computer scientists into true believers too. They believe in quantum entanglement, so much so that it’s a conviction, and nothing can shake that conviction. Instead of looking carefully at the evidence, they too end up peddling the snake oil, and governments end up wasting billions on “quantum technologies” that have never delivered anything, and never ever will. Yes this needs to be spread widely. I will be interested to hear of your experience when you try to do that. I suspect it will not be a heartening experience. I suspect trying to tell somebody that there is no quantum entanglement will be like trying to tell a suicide bomber that there aren’t 72 virgins waiting for him in paradise.
I have dug into this more. Regarding Bells Inequality, optics, polarizers and Malus law it really boils down to this:
The intensity of an electromagnetic wave is proportional to the square of the amplitude of the wave. So when using a polarizer the ratio of transmitted light to incident amplitude is a function of cos ϕ, but the ratio transmitted light to incident intensity is cos^2ϕ
Idiots are intuitively and naively thinking that the detected intensity should be a function of Cos ϕ (and this is the linear straw mans control example for ‘hidden variable’ classical prediction in experiments testing Bells Inequality), but in fact the detected intensity is a function of Cos^2 ϕ (which is what is experimentally found and true but has nothing to do with quantum entanglement!).
First off, these Bells Experiments with polarizers are simply remonstrating a phenomenon (Malus Law) which was discovered in 1808. Second, these Bell experiments have absolutely nothing to do with quantum entanglement or action at a distance and do not prove quantum entanglement or action at a distance in any way. These Bell Experiments with polarizers could be reproduced with a single polarized beam and do not need any entangled particles or split beams/dual detectors.
I cannot believe that physicists have been fooled by these ridiculous arguments and experiments.
Can you look into the CHSH game? My brief review is that the CHSH game results actually also come down to exploiting the benefit of an EPR pair using logic argument, so it is somewhat circular in that assuming you have an EPR pair then you can exploit that logically. But you can’t prove quantum entanglement on paper! When they went to test it I think they went back to polarizers and thus fell into the same trap of ‘rediscovering’ Malus law, and assuming a result which violates Malus law as the expected results for a classical local realism model. So again boils down to: First they assume a result which violates Malus law as the classical local realism model results, then they find that Malus law holds true, and so somehow that proves quantum entanglement? Such a crock and ridiculous argument.
Dear Andy,
Thank you for your comment. The idea of “entanglement” of photons stems from the wrong idea of Alain Aspect about the “naive” correlation function being zig-zag like function (with special points of non-existing derivative at 0 and 90 degrees). See the article here:
https://arxiv.org/pdf/quant-ph/0402001
Mathematicians demonstrated long ago that the correlation function between any vectors is a function of Cos(angle):
.Zenon Gniazdowsi “Geometric interpretation of correlation” // Zeszyty Naukowe Warszawsiej Szkoly Informatyki, No 9, Vol.7, 2013 p.p.27-35.
This Cos angle is the consequence of Pythagorean theorem and will be present in 3D even in Lobachevsky or Rimann curved spaces because the effect is local and any curved space is locally Euclidean. Only in one-dimensional case the correlation function will be zig-zag indeed.
I wrote this critique in my blog here:
https://tipikin.blogspot.com/2019/08/about-correlation-function-between-two.html
Alain Aspect unified three different phenomena under one umbrella:
1.The real quantum superposition (well known effect, known from Rabi oscillations and used in magnetic resonance, in Q-bits, in Josephson’s circuits etc)
2.The trick of synchronization of two resonators using the polarized light.
3.The non-existing “entanglement” of photons, which he “discovered”, re-inventing Malus law:
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.47.460
In his first publications he used the photons from Ca2+ two photons decay, the photons are not even the same (first in cascade has wavelength of 551.3 nm and second one 422.7 nm and they are only approximately in the same polarization because the life time of the intermediate state in two-photons fluorescence is 4.7 ns.
Indeed, no real “entanglement” of photons was ever discovered. It is necessary to emphasize that the quantum superposition is real quantum phenomenon, “privatized” by Alain Aspect under his “entanglement” umbrella.
Thanks Dmitriy! This is exactly it. Yes, you state it much more elegantly than I in your blog post. How could Alain Aspect not get challenged on this? He was working at the Institut d’Optique which is the Institute of Optics! There is no way he didn’t know about Malus law and basic optical transmission through polarizers. The title of his paper is so ridiculously ironic, “THE NAIVE VIEW OF AN EXPERIMENTALIST”, well it is certainly Naive, or worse willfully omissive. How can this be allowed to stand, especially with the recent Nobel prize? Academics usually jump at the opportunity to make a name for themselves, wonder why someone hasn’t stood up yet to call BS to this whole series of experiments, and explain exactly why for others to review?
Andy: Aspect referred to Malus’s law in Bell’s Theorem : The Naive View of an Experimentalist. It’s on page 5.
Andy: your example with the apples was already covered by Bell in a paper, he uses a pair of socks instead. Bell was not stupid like you make him sound. In fact, you simply didn’t understand what the real issue is.
.
One of your boxes goes to Miami, the other stays with you at San Francisco. You and your Miami friend open the box and find, as expected, two compatible halves of the apple (in Bell’s example, one right handed and one left handed sock) 100% of the time.
.
Now you repeat the experiment, but instead of Miami you send the box to Singapore. You open again your boxes, and find this time the halves are identical, meaning two left handed socks (or two right handed socks), 100% of the time. But the boxes are exactly the same as before.
.
This is just one of the many issues with the idea. There are ways to make this “sign flip” happen, but you will never reach full agreement with QM for all angles.
.
Malus law does not work. I’ve explained this to the detective over 3 times, but he’s adamant in his belief, not unlike the believers in Bell’s theorem. Malus law has the form cos^2(theta), where theta is the angle between a polarizer and the electric field at that polarizer. For two such polarizers, the total coincidence probability is of course cos^2(theta)cos^2(theta-ab), where ab is the angle between detectors, and assuming the same hidden polarization angle for both photons. You can obviously see that this can never simplify to 1/2 cos^2(ab/2), which is the actual quantum mechanical probability for entangled pairs (except for the choice theta=ab/2=90°).
Andy: Malus’s law works just fine. However some people just want to believe in quantum entanglement. They want to believe in instantaneously spooky action at a distance, and they want you to believe it too. So much so, that they will evade the patent fact that the two cascade photons were never entangled in the first place. They will give you a garbled version of Malus’s law, dodging the way it involves two polarizers as per the first illustration above. They will also dodge the fact that a polarizer transmits half of the incoming randomly polarized light. Then if all else fails they will tell you that you do not understand what Bell was saying. Unfortunately for them, I do. Like I said in Quantum entanglement is scientific fraud, Bell employed sophistry, sleight of hand, and deliberate confusion to claim that polarizers are subject to probabilistic summation as per the blue diagram. He wilfully ignored Malus’s law, and the way the three-polarizer trick proves that polarizer A alters the polarization of the local photon A, not the remote photon B.
Thanks to both of you. Sandra, I like my example of the apple being split much more than the socks, because socks are not “entangled” nor are they even chiral. In my example there are only 2 different pieces and no other possibilities. I think what Bell may have been trying to do is use a item which is chiral, Left handed versus Right handed which cannot be superimposed, such as Gloves. However socks are not even chiral, they can be superimposed, so it makes that example quite pedestrian. So in some other world you think that you get 2 of the same socks 100% of the time but the boxes are exactly the same as before? Sounds like a magic trick! That can’t happen in my example with the apple, unless you believe in magical thinking. Hate you break it to you but magic does not exist.
You stated that “Malus law does not work”? Not sure what you mean here. No one is disputing Malus law, its an empirical and mathematical fact stemming from the dot product of two vectors. You can conflate it and play logic games with 2 detectors or 4 detectors and split the beam, but its all just mumbo jumbo, because the tests did not even have or use a truly entangled pair if that even exists.
Andy: I’ve had a good old look at what Bell said about socks. See Bertlmann’s socks and the nature of reality. His figure 6 depicted the rotation by the Stern-Gerlach apparatus, which is akin to the rotation performed by a polarizing filter. But he didn’t talk about that. He talked about quantum mysticism instead. The more I found out about Bell, the more I thought he was a charlatan on the make.
Andy: Bell specifically used pink and (I believe) blue socks. I changed to make the example a bit closer to spin experiments. But you should read the example by Bell himself. In any case the issue here is that you can’t consistently cut the same apple up and get the correct correlations.
.
“Malus law does not work” to explain entanglement correlations, where two fermions (or photons) are sent to oppositely placed detectors. That’s the setup of EPR tests. The probabilities provided by applying Malus law, taken as isolated events at each detector, simply do not multiply correctly to give the exact quantum mechanical prediction.
.
There have been dozens of EPR experiments. The one you mention by Aspect et al was done in the 80s. 40 years ago. We can cut Alain some slack for the issues in that particular experiment now can’t we? Besides, what was demonstrated is a clear cut QM prediction. If you believe that is a wrong prediction, then you’re basically believing all of QM is wrong, at least after Dirac.
.
Again, if you didn’t understand my argument about the probabilities, I urge you to read the derivation and definitions from Bell himself, which the Detective kindly linked in the article.
Detective: as you always do, you’re skirting the issue. You implicitly (and incorrectly) state that I *want* to believe in entanglement. I also believe entanglement is absolutely wrong. But I also understand the nuance of Bell’s theorem, of which you clearly have only a superficial understanding. You keep referring to a 1981 experiment as if it was the only experiment ever performed to prove quantum correlations. You keep repeating “malus law explains it”, when it is clear as day that even outside entangled pairs simple probability arithmetic fails to produce the correct probability.
You keep repeating stuff for years and years, and yet, your understanding of it never seems to go anywhere, despite repeated corrections. Interestingly, you never quite went down the actual history of how Bell came to produce his theorem or the motivation driving him, and all the other related theorems like Kochen-Specker, or even von Neumann where it all started. Perhaps you should, you might learn everyone can be wrong sometimes.
Sandra: the key phrase in the above is “of which you clearly have only a superficial understanding”. Insults do you no credit. Look, I don’t quite know how else I can spell this out, but it goes something like this: Bell was a charlatan peddling blarney and bullshit to try to make his “Einstein was wrong” name. He got lucky via Clauser and Freedman then Aspect, who performed experiments with cascade photons that weren’t even entangled. As you know full well. So please stop peddling the myth and mystery. It does not go down well here.
I have read both of your comments and long prior discussions on this. Maybe I can be the referee here. Sandra if you believe as you just said that “entanglement is absolutely wrong”, then that is great. I agree with you on that as well. Would you also agree then that the entire series of experiments testing Bell’s Inequality were basically pointless if there is no entanglement or entangled particles being used? On the other hand I agree with you Sandra that technically Johns description of the split dual simultaneous polarizers and detectors in parallel being the same as a single beam through 2 sets of polarizers in series is not exactly true. In the parallel setup each photon interacting with only 1 polarizer, where in the series the photon is interacting with 2 polarizers. I am not sure it makes any difference though and they are effectively the same, and if there is no entanglement then it doesn’t matter anyway right?
Detective: that was not an insult. It was just a statement about basic facts which everyone can read. It carried absolutely no significance for your persona. Having a superficial understanding is not insulting, what is is refusal to better one’s understanding. You still skirt the issue I pointed out. Are you completely, genuinely convinced Nobel laureates, PhDs, and the vast majority of people working in the foundations of QM would not understand the simple argument you point out in your blogposts? Mind you, they can still be wrong about entanglement, nobody is questioning that.
.
Well you’re still convinced people don’t understand GR so I wouldn’t be surprised. This kind of conspiratorial, “I am the only one that gets it” attitude is usually carried by those you yourself call charlatans. You’re better than that.
.
Andy: the point of experiments is that they proved a quantum mechanical prediction. It’s the interpretation of that prediction (reality of superposition, non-locality, fundamental woo) that is wrong. There is a way to make sense of the correlation, without questioning their existence which HAS been proven experimentally, but it doesn’t involve simple arguments like those of the Detective. For one, it requires complete understanding of the assumptions that go into Bell’s theorem, like statistical independence, Reichenbach (I believe that is the name) causality, “realism” in the EPR sense, and additivity of expectation values, and also it requires an understanding of what the operational definition of a hidden variable theory is (a description of quantum mechanics with dispersionfree states, where eigenvalues of operators are unique).
Sandra: do excuse me if I consider having a superficial understanding to be an insult. Particularly after I’ve been through Bell’s papers line by line. As for you’re still convinced people don’t understand GR, I’m not the one with the convictions. I’ve had three conversations recently where all three respondents absolutely refused to countenance “the speed of light is spatially variable”. Even when I tried to show them the Einstein quotes. That’s because they are convinced that the speed of light is constant. As a result they believe that light curves because it follows the curvature of spacetime. Or that a black hole drags light back. Or that a gravitational field is a place where space is falling down as per the waterfall analogy. Or that a black hole offers a route to the parallel antiverse. Or that a black hole can be used for time travel. All of these things are wrong. Because people like Wheeler, Hawking, Tegmark, Penrose, and Thorne, plus others, did their own thing and ignored what Einstein said. Along with the hard scientific evidence that optical clocks go slower when they’re lower. If you’d like to discuss it further please add a comment to the speed of light is not constant thread or the how gravity works thread.
Detective: I have no qualms about the speed of light being variable, if anything because the speed is not even a globally definable quantity in GR, like energy. Instead what you do in GR is talk about geodesics. I don’t want to discuss it further as that’s not the topic at hand, despite you repeatedly ignoring my inquiry and trying to derail the conversation.
.
If you went line by line in Bell’s writings, then you should know about his motivation for pursuing hvt, in a period where that was taboo in scientific discourse. It was Bohm’s theory, whose sole existence was in conflict with “settled mathematics”, i.e. von Neumann’s theorem. Now we know that theorem is wrong, and mostly thanks to Bell (the first actually was Grete Herman and Einstein after her, but they were essentially ignored). He wasn’t, as you put it, promoting “quantum mysticism […]. The more I found out about Bell, the more I thought he was a charlatan on the make”. His intention was exactly like yours, he was going against the mainstream. There’s a plethora of interesting anecdotes about Bell questioning his own result until the very end, unlike current “philosophers” which seem to accept it without second thought.
.
So you see, the issue has nuance. A nuance you completely and repeatedly dismiss. Malus law ain’t it, and more than showing you the mathematics, logical arguments or even showing you the history I can’t do.
Sandra: re GR, the important point to note is that the spatially variable speed of light means that people like Wheeler, Hawking, Tegmark, Penrose, and Thorne are all wrong. So much so that they end up promoting fantasy physics. See my article on black holes for more. So I’m afraid it’s true that people don’t understand GR. Perhaps you’ve now realised I’m right about that. Is that why you don’t wish to discuss it further, even though you raised the matter?
Re your question: “Are you completely, genuinely convinced Nobel laureates, PhDs, and the vast majority of people working in the foundations of QM would not understand the simple argument you point out in your blogposts?” I think some of them do not wish to even consider the simple argument, just as my three contacts refused to consider the spatially-variable speed of light. I also think some of them understand that cascade photons are not even entangled, that the local polarizer alters the local photon, and that cos² θ applies when photons go through two polarizers like this → → as per Malus’s Law, or like this ← → as per a Bell test. So they know that Bell’s straight line prediction was always straw man sophistry. But they will never admit it.
I’m sorry Sandra, but you have provided nothing to counter this. Instead you have avoided what is a simple issue, and attempted to persuade via bulky comments laden with distraction. As to what, I’m not quite sure, because you are now saying “I also believe entanglement is absolutely wrong”. Do feel free to explain why, or point me to a previous comment where you have explained it. Apologies in advance if I did not pay enough attention previously. I tend to be continually short of time.
Detective: I don’t want to discuss GR because 1) that’s not what this blogpost is about (I just only mentioned it as a comparison, but you decided to cling on to it for some reason) 2) it’s not my expertise, so I don’t feel it to be correct to point out mistakes, although I do understand the basics of differential geometry and know how to make simple arguments in the mathematics of GR instead of just using rethorics.
.
“I think some of them do not wish to even consider the simple argument” probably because it’s the first argument they’ve ever come across while studying Bell’s theorem (it’s one of Bell’s toy models) and understood rather fast that it doesn’t work. I’m here considering it, and replying to you that it’s wrong. Why would you expect someone else to give a different answer?
.
“cascade photons are not even entangled” – again referring to a single out of dozens of experimental tests.
.
“the local polarizer alters the local photon, and that cos² θ applies when photons go through two polarizers like this → → as per Malus’s Law, or like this ← → as per a Bell test.” except those two are completely, utterly different physical setups. In the first setup you have one particle, in the second one you have two, in a singlet state. I hope you know what that entails.
.
“So they know that Bell’s straight line prediction was always straw man sophistry.” What exactly would all these conspirator have to gain by lying about Bell? Aside from aspect et al who won the nobel. That’s a tinfoil hat right there.
.
” you have avoided what is a simple issue” that’s gaslighting to 9000. Never avoided it, you just ignored my criticism of your perceived issue.
.
But this is all beside the point. Your “malus law” simply would not even apply for fermions in a stern-gerlach apparatus. You state that case “is similar” without elaborating. It’s just not. There’s no electric field intensity, no blocked particles, no polarizers, no malus law.
Sandra,
I think you are just arguing to argue and changing the topics. You yourself said that you don’t believe that entanglement exists here is your quote from just a few posts back:
Sandra 22ND APRIL 2025 Reply: … “I also believe entanglement is absolutely wrong.” …
Ok so if you believe entanglement is absolutely wrong then there is no point to Bell’s experiments. End of Story. You seem then to be arguing some technical component of the experiment since you don’t believe in the conclusion. The conclusion of the series of Bell’s experiments was that quantum entanglement exists. You state you believe entanglement is absolutely wrong. So why don’t you reconcile your beliefs and arguments internally with yourself before continuing to post the same thing repeatedly.
I for one would much rather John spend his time reading, researching, thinking about new issues, and posting new articles instead of replying back to you when you are rehashing the same issue over and over.
Andy: omg. Changing the topics? What are you talking about? Obviously by “entanglement is wrong” I mean spooky action. Superposition. Non-locality. It is not hard to understand. Why would not believing that woo invalidate the experiments? QM predicts a cosine correlation for coincidence counts equal to 1/2cos^2(theta). Malus law can’t give you this result. Experiments have verified this correlation is correct. Many physicists believe that is proof of spooky action, I don’t. Detective thinks Bell is a charlatan, he’s free to believe so. To borrow one of his quotes, you can bring the horse to the water, but you can’t force it to drink.
.
“John spend his time reading, researching, thinking about new issues” you mean rehashing the same trite quotes blogpost after blogpost? Listen, take some advice. Instead of reading this…whatever it is, go read “Speakable and unspeakable”.
Please pass the popcorn 🍿; this episode of “As the Physics World(s) Churn!” is a really hot 🔥 barn burner !