The standard model of particle physics is said to be a gauge theory. It’s made up of different sectors, including the electroweak sector which is said to be a Yang-Mills gauge theory. The Encyclopaedia Britannica electroweak theory article says it “arose principally out of attempts to produce a self-consistent gauge theory for the weak force, in analogy with quantum electrodynamics”. Quantum electrodynamics is the theory that says the electron is a point-particle, that electrons and protons interact by throwing photons at one another, and that photons don’t interact with photons. We know about quantum electrodynamics. But what’s a gauge theory?
What’s a gauge theory?
The Wikipedia gauge theory article defines it using mathematical terms that aren’t defined locally, so it isn’t ideal. The Wikipedia introduction to gauge theory article isn’t ideal either. It says a gauge theory is one where fundamental fields can’t be directly measured, but different configurations of these unobservable fields can result in identical observables. It also says a transformation from one unobservable field configuration to another is a gauge transformation, and the unobservable effect of changing these unobservable fields is called gauge invariance or gauge symmetry. That doesn’t sound good. However the article does say “the importance of gauge theories for physics stems from their tremendous success in providing a unified framework to describe the quantum-mechanical behavior of electromagnetism, the weak force and the strong force”. So a gauge theory is to do with unification. That does sound good:
 Image by Paul Langacker, see Grand Unification on Scholarpedia
Image by Paul Langacker, see Grand Unification on Scholarpedia
Particularly since the introduction to gauge theory article also talks about electromagnetism, which is in itself an example of unification. That sounds good too. If we can understand why electromagnetism is a gauge theory, then perhaps we can move on to other gauge theories later. What’s not so good is that the article hardly mentions the electromagnetic field, and when it does, it says the electromagnetic field doesn’t interact with itself. Instead it says electric and magnetic fields E and B are observable, but the associated potentials V and A are not. Because “under a gauge transformation in which a constant is added to V, no observable change occurs in E or B”. That’s about as useful as saying when your skateboard rolls downhill, you can’t tell how high the hill is. So, time to dig out the deerstalker and start digging. Let’s look at some history.
Historical roots of gauge invariance
The story starts with electromagnetic unification. See the historical roots of gauge invariance by John Jackson and Lev Okun dating from 2001. They say the roots of gauge invariance go back to 1820 when the first electrodynamic theory was proposed. They talk about the freedom of choice of the scalar electric potential ϕ and the magnetic vector potential A, which was expressed in different competing forms. They say in 1857 Gustav Kirchhoff showed that the Weber form of A plus the scalar potential ϕ satisfied the relation ∇ · A = −∂ϕ/c∂t. That’s where the divergence of magnetic vector potential A equals the rate of change of scalar electric potential ϕ. Jackson and Olun say this was “the first published relation between potentials in what we now know as a particular gauge”. They also say Ludvig Lorenz’s contributions are significant, but that he’s often confused with Hendrik Lorentz. They say in 1867 Ludvig Lorenz established that retarded potentials satisfy what’s nowadays known as the Lorenz gauge condition: ∇ · A + 1/c ∂ϕ/∂t = 0. They say Lorenz remarked that the retarded potentials give the same fields as the instantaneous scalar potential and a vector potential, and that “without explicit reference, Lorenz was apparently aware of and made use of what we call gauge transformations”. They also say Hermann Helmholtz was close to establishing the gauge invariance of electromagnetism in 1870, and that in 1873 James Clerk Maxwell wrote what’s now called the gauge transformation equation A = A’ – ∇χ. They quote him saying “the quantity χ disappears from the equations (A) [B = ∇ x A] and it is not related to any physical phenomenon”. They also refer to Hendrik Lorentz and page 239 of his 1909 book, where “we find the first clear statement of the arbitrariness of the potentials under what we now call general gauge transformations”.
Electromagnetism is a gauge theory
This fits in with what Gerard ‘t Hooft says in the Scholarpedia gauge theories article. He says the simplest example of a gauge theory is electrodynamics, as described by the Maxwell equations. He refers to ϕ and A, and says electrodynamics is a gauge theory because the values of these potential fields are not completely determined by Maxwell’s equations, and “one can find a different set of potential fields describing the same electric and magnetic fields”. David Gross is of the same opinion in his 1992 paper Gauge Theory – Past, Present, and Future? He says gauge theory first appeared in Maxwell’s formulation of electrodynamics in 1864, but that “the symmetries of this theory were not truly appreciated for many decades”. He says electromagnetism contained two important symmetries, Lorentz invariance and gauge symmetry, but both went unrecognized. He goes on to say Lorentz invariance required the conceptual revolution of relativity.
Electromagnetism and relativity
Lorentz invariance in an electromagnetic context concerns electromagnetic four-potential, which is a unification of the scalar and vector potentials, typically denoted as Aμ = (ϕ, A). If you were a positron and I set you down near an electron, you might claim the electron had an electric field that caused linear motion. However if I threw you past the electron, you might claim the electron also had a magnetic field that caused rotational motion too. But note that when I changed your motion relative to the electron, I didn’t change the electron’s field. This ought to make it plain that the electron doesn’t have an electric field and a magnetic field, it has an electromagnetic field. Hence Einstein’s 1905 paper on the electrodynamics of moving bodies where he said electrodynamics as presently understood leads to asymmetries such as the moving magnet and conductor problem. Hence in 1908 Hermann Minkowski said this in Space and Time: “In the description of the field caused by the electron itself, then it will appear that the division of the field into electric and magnetic forces is a relative one with respect to the time-axis assumed; the two forces considered together can most vividly be described by a certain analogy to the force-screw in mechanics; the analogy is, however, imperfect”. It’s one type of field and two types of force. The electron has an electromagnetic field, as does the positron. And electromagnetic field interactions between charged particles result in linear electric force and/or rotational magnetic force because it takes two to tango:
 New South Wales dept of education image see nsw.edu.au CCASA image by Stijn Lichtert, see Wikipedia
New South Wales dept of education image see nsw.edu.au CCASA image by Stijn Lichtert, see Wikipedia
Hence the electromagnetic field is a dual entity wherein electric and magnetic fields are two parts of a greater whole. See section 11.10 of Jackson’s Classical Electrodynamics where he says E and B have no independent existence, and that a purely electric or magnetic field in one coordinate system will appear as a mixture of electric and magnetic fields in another. He also says “one should properly speak of the electromagnetic field Fµv rather than E or B separately”. And since there’s one field there’s only one potential. That’s why in section 25-4 of the Feynman lectures you can read that “the scalar and vector potentials are really different aspects of the same physical thing”. The same applies for electromagnetic waves. See the Wikipedia electromagnetic radiation article and note that “the curl operator on one side of these equations results in first-order spatial derivatives of the wave solution, while the time-derivative on the other side of the equations, which gives the other field, is first order in time”. The electric field variation of a photon is the spatial derivative of four-potential, whilst the magnetic field variation is the time-derivative. Hence the Lorenz gauge. It’s like you’re in a canoe at sea and a sinusoidal tsunami comes at you. Your canoe tilts up and the degree of tilt denotes E whilst the rate of change of tilt denotes B. Sadly when you read about gauge theory you often find electric and magnetic fields described as if they’re two totally different things.
Electromagnetism was unified over a hundred years ago
This is a shame, because you can find people like Gustav Mie talking about four-potential over a hundred years ago. See his 1913 Foundations of a theory of matter translated by David Delphenich. In chapter 1 section 4, Mie talked of “the so-called ‘four-potential’ that one constructs from the scalar potential j and the vector potential f.” He said “the two potentials, j and f, embody the physical state of the universal ether”. He said ether rather than space, but no matter, because Einstein was talking of space as the ether of general relativity in 1920. Interestingly Mie also said electrons “are not distinct from the ether. They are not, as has been believed for twenty years, foreign particles in the ether, but they are only places at which the ether takes on a particular state that we give the name of electrical charge”. It’s good stuff. Particularly since chapter 2 is Knot Singularities in the Field. I think it’s a pity more people don’t know about this sort of thing. Or that the symmetry of the moving magnet and conductor problem is due to the screw nature of electromagnetism.
The rise of symmetry
Talking of which, see the role of symmetry in fundamental physics by David Gross again, dating from 1996. He says Newton’s laws embodied symmetry principles which implied conservation laws. He says Maxwell’s equations “embodied both Lorentz invariance and gauge invariance. But these symmetries of electrodynamics were not fully appreciated for over 40 years or more”. He goes on to say the situation changed with Einstein’s great advance in 1905, which was to put symmetry first and derive the transformation properties of the electromagnetic field from relativistic invariance. Gross says this was the first instance of the geometrization of symmetry. He also says this approach scored a spectacular success with general relativity, where “the principle of equivalence, a principle of local symmetry – the invariance of the laws of nature under local changes of the space-time coordinates – dictated the dynamics of gravity”. The trouble with that is that the principle of equivalence only applies to a region of infinitesimal extent. To no region at all. Einstein’s happiest thought led to a useful line of reasoning, but it was merely a ticket to be discarded at his destination. As John Synge said, the principle of equivalence performed the essential office of midwife at the birth of general relativity, but the midwife now needed to be buried. That’s because standing in inhomogeneous space might feel similar to accelerating through homogeneous space, but it is not the same:
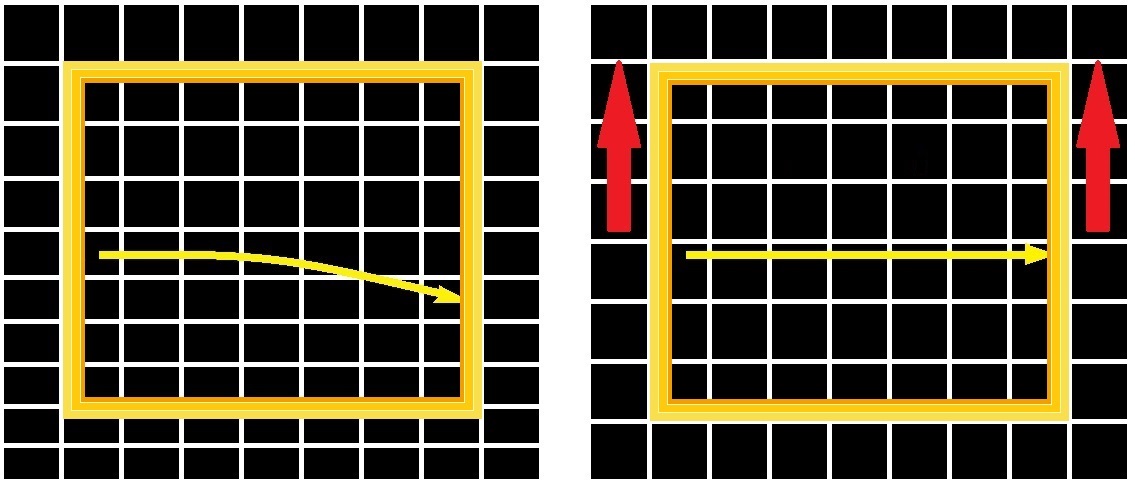 Reference frame pictures by me
Reference frame pictures by me
One can find similar issues with the way Gross presents Noether’s theorem. He says momentum is conserved due to the invariance of the laws of physics under spatial transformations. But the laws of physics have no real existence. They merely describe the things that do. And those things that do, do what they do because of the way they are, not because of mathematics. There’s an English translation of Amalie Noether’s 1918 paper on the arXiv. It’s called Invariant Variation Problems, it’s very heavy going, and there are issues. See the Mathspages article on Noether’s theorem. It says conservation of energy is closely related to the time-invariance of physical laws, but in general relativity there isn’t a global time coordinate. Energy is conserved because it is what it is, not because of some symmetry, and it’s conserved in a gravitational field too. See Gustav Mie talking about that in 1915 in The Principle of the Relativity of the Gravitational Potential: “when two gravitating masses approach each other, there is on the one hand an increase in the energy of the field, counted as positive exactly like that of an electric field of similar appearance, but at the same time there is a change, a decrease to be exact, in the internal energy of the approaching material bodies”. In extremis this creates a gamma-ray burster issue for conservation of charge, which is said to be due to gauge invariance. Hermann Weyl was responsible for that. He invented gauge theory.
Hermann Weyl invents gauge theory
Weyl wrote a paper on gravitation and electricity in 1918. He talked about parallel transport and said the final direction of a vector depends on the path taken. Then he said there’s no good reason why the final length shouldn’t vary too. He said this on page 2: “On the removal of this inconsistency there appears a geometry that, surprisingly, when applied to the world, explains not only the gravitational phenomena but also the electrical. According to the resultant theory both spring from the same source, indeed in general one cannot separate gravitation and electromagnetism in an arbitrary manner”. I think he was spot on. But I think it’s unfortunate that he said “corrected” in this sentence: “I shall first sketch the construction of the corrected Riemannian geometry without any reference to physics”. He then gave three rather mathematical pages which ended up with expressions that resemble electromagnetic equations, and on page 5 said “it’s very suggestive to interpret ϕ as the electromagnetic potential and the tensor F as the electromagnetic field”. He also said “one sees that electromagnetic quantities are such that their characterization by numbers in a given coordinate system is independent of the scale”. That’s a must if lengths are changing. But he then gave three more rather mathematical pages which don’t seem to develop his argument. On page 6 he said “continuously parallel-transferring the vector in its own direction”, which is good. But he also said “the concept of length along a curve is not meaningful”, which isn’t. On page 7 he said “only in Euclidean space is there neither electromagnetism nor gravitation”, which is good:

But on page 8 he said “in four dimensions the electromagnetic action is a pure number”, which isn’t. Then he said “passing on from the geometry to the physics”, but there isn’t any physics. He did refer to Gustav Mie’s theory and say the whole set of natural laws are based on an integral-invariant action, but there’s no experimental justification. Hence when on page 9 he said “the electromagnetic conservation law is connected with the new scale-invariance”, it isn’t convincing. That’s perhaps unfortunate, but I think what’s really unfortunate is this on page 11: “But in fact it is not very probable that the Einstein gravitational field equations are strictly correct”. He was saying Einstein was wrong. Which presumably is why there’s the rather unusual postscript from Einstein. Einstein said this: “If this were really so in Nature, chemical elements with spectral-lines of definite frequency could not exist and the relative frequency of two neighbouring atoms of the same kind would be different in general. As this is not the case it seems to me that one cannot accept the basic hypothesis of this theory”. Einstein’s also said “whose depth and boldness every reader must nevertheless admire”, but the damage was done. Weyl’s ideas didn’t get corrected, they got rejected.
Did Weyl screw up?
Check out Komaravolu Chandrasekharan’s centenary lectures for more. Or see William Straub’s Weylmann.com website. Straub gives two essays on Weyl’s 1918 theory. He says Weyl saw this regauging of the metric as a new beautiful type of symmetry which would hopefully show that electrodynamics like gravitation was a geometrical construct. It surely is, but it’s more than just a change of scale. There’s pair production and the wave nature of matter and spin ½ spinors and linear and rotational force because it takes two to tango. Straub asks Did Weyl screw up? and I think the answer is yes. But only because he was critical of general relativity and Einstein. Of course there were some other minor issues, like Weyl didn’t understand the electron, or how electromagnetic and gravitational forces actually worked. I think this is clear enough if you read Weyl’s 1919 paper. David Delphenich has again provided a translation. The title is a new extension of the theory of relativity. It’s long on abstract mathematics and short on factual physics, and it doesn’t distinguish between curved spacetime and curved space. Yes, the theory “would fulfil the dream of Descartes of a purely geometrical physics”. But the foundation is lacking, which is perhaps why Weyl proposed a path-dependent length rather than a position-dependent length. And I’m afraid that as Straub says, Weyl’s mathematical writing style could be exceedingly obtuse. It would seem that Paul Dirac and other physicists thought so too. So all in all, Weyl’s gauge theory did not take off. Nobody pursued the idea, least of all Einstein. Even though with his purely geometrical physics Weyl was definitely barking up the right tree. The geometry of the world is surely there because of rescaling. In simple terms, if all your lattice elements are the same length, there is no curvature in your lattice:
 Photon four-potential picture by me
Photon four-potential picture by me
Lochlainn O’Raifeartaigh and Norbert Straumann give more information in their 2000 essay Gauge theory: Historical origins and some modern developments. They say Planck and Sommerfeld reacted positively, but that Planck then changed his mind. They also say that in 1921 Wolfgang Pauli was critical, saying “in summary one may say that Weyl’s theory has not yet contributed to getting closer to the solution of the problem of matter”. As to how much professional jealousy was at work I don’t know. But Einstein was still critical in 1921, which is when Weyl gave up on his idea.
All was not lost
However all was not lost. Vladimir Fock wrote a paper in 1926 on the invariant form of the wave and motion equations for a charged point mass. According to Jackson and Okun, Fock “extended the known freedom of choosing the electromagnetic potentials” to quantum mechanics. Fock referred to a paper by Heinrich Mandel which used “the notion of five-dimensional space in order to consider gravity and the electromagnetic field from a unified standpoint”. He said the introduction of a fifth coordinate facilitates representation of the Schrödinger wave equation in an invariant form. And that “the role of the additional fifth coordinate parameter p is precisely to ensure the invariance of the equations under the addition of an arbitrary gradient to the four-potential”. He didn’t refer to Weyl, he was coming up with his own version of the Klein-Gordon equation. Helge Kragh gives the history in his 1984 essay Equation with the many fathers. The Klein Gordon equation in 1926. A variety of physicists came up with the Klein-Gordon equation in an attempt to model the electron, including Oskar Klein in a 5D unification paper, and Walther Gordon in a paper on the Compton effect. However the Klein-Gordon equation didn’t work because it models massive spinless particles, and electrons have spin. Jackson and Okun say Fock said for the dynamics to remain unchanged by transformations A = A1 + ∇f and ϕ = ϕ1 – 1/c δf/δt, the wave function must undergo the transformation ψ = ψ0e2πi p/h whereby it’s multiplied by a local phase. That fits with the canoe analogy: the altitude of your canoe relates to its tilt and how far you’re into the sinusoidal tsunami. Interestingly the Klein-Gordon equation for a free particle has a simple plane-wave solution, and an example of a phase shift can be found in what’s known as the Aharonov-Bohm effect. This was first predicted by Ehrenberg and Siday in their 1949 semi-classical paper The Refractive Index in Electron Optics and the Principles of Dynamics. See their figure 2. The lines depict electron plane waves where the phase is advanced on one side of a solenoid and retarded on the other:
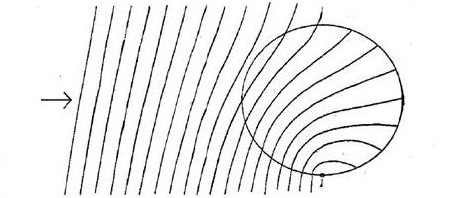 Image from Ehrenberg and Siday’s The Refractive Index in Electron Optics and the Principles of Dynamics 1949.
Image from Ehrenberg and Siday’s The Refractive Index in Electron Optics and the Principles of Dynamics 1949.
See the AIP oral history interview where Fock talked to Thomas Kuhn in 1967. Fock said “we all read De Broglie’s paper in ‘23 or ’24 on waves of matter”. And that there was an attempt by Weyl to introduce Goud’s difference in relativity. Fock said he was inspired by Weyl’s work, but “the right place for Weyl’s differential form was just the exponent – the face of the wave function and not the Goud’s”. I would hazard a guess that Fock had a thick Russian accent, and that Goud’s means gauge whilst face means phase. As for the distinction between gauge and phase I’m not so sure, because in the picture above, and in the picture on the previous page, the distance between the lines varies as the phase shifts. By the by you can read in the 2006 Fock biography by John O’Connor and Edmund Robertson that Fock “objects to the notion that invariance under general coordinate transformations is a property of the physical universe. He regards this invariance as merely a property of the mathematical symbolism, which it may be sometimes convenient to maintain and sometimes inconvenient”. They were quoting Freeman Dyson’s review of Fock’s 1955 textbook Theory of space, time and gravitation. Fock also disliked Einstein’s general principle of relativity and “violently objects to the principle of equivalence”. See page 232. It would seem Fock was something of a realist.
Fritz London to the rescue
Another contributor to gauge theory was Fritz London. As you can read on Wikipedia, he co-wrote the book on chemical bonds with Walter Heitler. He also co-wrote a paper in 1927 on the interaction between neutral atoms and homopolar binding according to quantum mechanics. Note the final paragraph, which says “we would like to thank Prof. Schrödinger for the kind and stimulating interest with which he has supervised our work”. Erwin Schrödinger had written a paper in 1922 on a remarkable property of the quantum orbits of a single electron where he’d commented on Weyl’s idea. Also note what the Wikipedia article says: “London was also one of the early authors (including Schrödinger) to have properly understood the principle of local gauge invariance (Weyl) in the context of the then new quantum mechanics”. London was also responsible for London forces, the plot for which resembles the nuclear force, and for ground-breaking work on superconductors. As far as gauge theory goes, his important paper was Quantum mechanical interpretation of Weyl’s theory written in 1927. There’s an English translation on page 53 of John Taylor’s 2001 book gauge theories in the twentieth century. London started by saying this: “As is generally known, recently the idea of a “purely local geometry”, first conceived by Riemann, has been completed by Weyl in a remarkably beautiful and simple way”. He said Weyl made the ansatz for a change of a length scale, and “by logically extending the geometric interpretation of gravitation as a variable curvature in Riemannian space, Weyl imagined the remaining type of physical forces, the electromagnetic field, also as a property of the scaling relations of space, characterized by the variability of the gauge scale”. London also said “one must admire the tremendous courage with which Weyl tracked down his theory of the gauge-geometric interpretation of electromagnetism”. He said he wouldn’t dwell on the development of Weyl’s theory, but would show that it contained even more possibilities than has been used by its author. London said “one has to view it as not less than the logical path to wave mechanics, and only in the light of this does it gain a directly comprehensible physical meaning”. London talked about de Broglie and Schrödinger, and much else, and ended up saying “the physical object, which behaves as Weyl’s measure, is found: the complex amplitude of the de Broglie wave”. A complex amplitude is also known as a phasor. See the Wolfram Mathworld rotation of spinors article where you can read that “in the course of rotation of ϕ by 4π, the phasor traces out a Möbius band”.
Herman Weyl’s 1929 paper
Weyl then wrote his 1929 paper Elektron und gravitation I. As far as I know the only English translation is on page 121 of Lochlainn O’Raifeartaigh’s 1997 book The Dawning of Gauge Theory. It isn’t generally available online, but there is a related paper called Gravitation and the Electron. On page 1 Weyl said “mass is a gravitational effect: it is the flux of the gravitational field through a surface enclosing the particle in the same sense that charge is the flux of the electric field”. Unfortunately it isn’t true. The mass of a body is a measure of its energy-content, and its resistance to change-in-motion. Gravity is nothing to do with it. On page 2 he said “Instead of one law for the conservation of charge we must have two, expressing the conservation of the number of electrons and protons separately”. That isn’t true either. In the next paragraph he referred to h/mc as the “wave-length” of the electron, in quotes. He didn’t seem to know that the electron really has a wavelength. Then he said the velocity of light c is determined as an absolute measure of velocity by the theory of relativity. This suggests he didn’t know that the speed of light varies with gravitational potential. Which is perhaps why he said the introduction of the atomic constants had removed the support for his principle of gauge-invariance. So he settled for a consolation prize and said “it possesses an equivalent in the field equations of quantum theory which is its perfect counterpart in formal respects”. He said the action integral is unaltered by the infinitesimal variation δψ = iλ · ψ and δϕp – δλ/δxp and that this is a new principle of gauge invariance.
Phase change ghosts
What does this mean? The ψ is electron wavefunction, whilst ϕp is four-potential. Weyl was saying if you change them both just so, there’s no observable change. Like I said earlier, that doesn’t sound too good, and I’m not the only one to say that. In the role of symmetry in fundamental physics Gross quotes Eugene Wigner being critical of gauge invariance. See the last paragraph of page 22 of Wigner’s symmetries and reflections. Wigner says “this gauge invariance is, of course, an artificial one, similar to that which we could obtain by introducing into our equations the location of a ghost. The equations must then be invariant with respect to changes of coordinates of that ghost. One does not see, in fact, what good the introduction of the coordinate of the ghost does”. Only it isn’t a ghost. Take a look at Walter Moore’s 1989 book Schrödinger, life and thought. On page 218 you can read that “as Dirac said later, the phase factor was very well hidden in nature”. It’s no ghost, it’s real. The Aharonov-Bohm effect proves it. It’s like what Gross says on page 2 of Gauge Theory – Past, Present, and Future: “accompanying the translation of charged particle there is a phase change”. Because of something fundamental. Something to do with unification. Wigner said “the combination of these two transformations, one on the electromagnetic potentials the other on the matter field, is called a gauge transformation”. Weyl said “If our view is correct, then the electromagnetic field is a necessary accompaniment of the matter-wave field and not of gravitation”. So what sort of unification could we be talking about?
What electromagnetic gauge theory is
When you ask what a gauge theory is, you tend to get contradictory answers. See for example Leo Stein’s answer on Quora. He says “gauge theory is any field theory in physics in which some global, continuous symmetry of the theory is promoted to a local symmetry. By doing so, a new field is introduced (the gauge field) which has its own dynamics and couples to the particles/fields which have the symmetry. Those particles are then said to be charged under the gauge field”. However that doesn’t help you to understand the real thing that’s there or the physical meaning of why electro-magnetism is a gauge theory. What does is Chen-Ning Yang’s 2014 article The conceptual origins of Maxwell’s equations and gauge theory. He talks about geometry and electromagnetism, and U(1) rotation and says Weyl’s length-change factor “should have been called a phase-change factor”. What does this mean? Imagine you have a sinusoidal electromagnetic wave. Imagine it’s just sitting there motionless in space and you’re standing in front of it:

If you take the derivative of a sine function you get a cosine function. It’s a wave that’s the same shape, but displaced by a 90° phase shift. Take the derivative of the cosine function, and you get another 90° phase shift. Apart from the phase shift the derivative is invariant, so the integral is too. And you could achieve the same result not by derivation, but by translation. You could walk to the right by half a wavelength. Now the height of the wave where you are, is different. There’s a change in distance and a change of phase. So, is there a phase change accompanying the translation of charged particle? Yes, but it’s not so obvious. It’s to do with gamma-gamma pair production, and invariant action h, and what the Wolfram Mathworld rotation of spinors article said about the phasor tracing out a Möbius band. Imagine your sinusoidal wave is made of paper which is lighter in colour on the reverse side. Give it longitudinal twist then bend the ends towards one another. Slide them along so they fit. Like a Möbius band. Like Dirac’s belt. Like this:
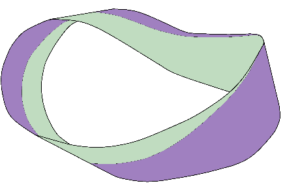
There is no width variation as you go round the strip, because at all locations round the loop there are two widths that add up to the same total width. But when you walk past it you perform a translation. Just as you performed a translation on the sinusoidal wave. And again there’s a phase change. It’s not so obvious, you need the Aharonov-Bohm effect to see it. It’s there because of the wave nature of matter. It’s why mass and charge always come hand in hand. Because when it comes to the electron, the matter wave is an electromagnetic wave. An electromagnetic wave in a spin ½ configuration. That’s the directly comprehensible physical meaning. That’s why electromagnetism is a gauge theory. Because there are no point particles. Which is doubtless why in his 1992 gauge theory essay, David Gross said “gauge symmetry, however, played almost no role in QED”.
Hmmm. I’ve followed all your posts up until this one John. But I’m still baffled by “gauge theory”. Why do I need it? What’s it for? Does it have anything to do with gauges (like the fuel gauge in my car, or the gauge of a railway track)?
Something about redundant degrees of freedom in a field? What’s it got to do with physics?
You write “when you walk past it you perform a translation …. And again there’s a phase change. … It’s why mass and charge always come hand in hand ….That’s the directly comprehensible physical meaning” … non-comprende 🙁
If I have a sine wave in front of me where the wiggles extend infinitely to my left and infinitely to my right, and I walk to the right by a quarter of a wave length then I can’t tell if I’ve differentiated the sine wave, or translated it, or if I’ve translated, or if a phase shift has been applied – I get that (is that Gauge Theory?? so what?). But if the sine wave in front of me is a single wavelength like in your picture and I move to the right, it does not look like a cosine wave. And although I understand the idea of the electron being a photon wrapped up in a double loop trivial knot, but if I move to the right of the electron its phase doesn’t change (what does phase mean anyway when you’ve got a single wavelength wrapped up in a mobius strip?). What changes is the electron is now on my left.
“Lorentz invariance”? What’s that for? Why do I need it? What’s it got to do with physics. What on earth is it? I was hoping to gets some insights into the neutron 🙁
“Gauge symmetry”? I’m still none the wiser on this.
Ummmm, it looks like this one’s a fail then Jonathan. I’ve just re-read it, and whilst there’s some good stuff in there, it doesn’t actually tell you what gauge theory actually is. Or that it’s a load old cobblers. Or that people have been trying to rewrite history by saying electromagnetism was the first gauge theory. I’ll make a note to do something about that. But like I was saying, life is hectic at the moment. How about if you ask What is gauge theory? or Why is electromagnetism a gauge theory? on Quora or Physics Stack Exchange? Or anywhere you can. See what they say. You’ll probably get nothing put handwaving and flannel, and you will be none the wiser. Alternatively, you could try reading this: Gauge theories -Scholarpedia by Gerard ′t Hooft. Note this: “What turns this theory into a gauge theory is the fact that the values of these potential fields are not completely determined by Maxwell’s equations”. It’s as if Maxwell’s unification never happened. The field is the electromagnetic field. It’s one field, not two. Underlying it is one potential, not two.
John, it seems that a guage theory is a theory that a wave construct or particle does not change under translation i.e. it is not changed in moving from one place to another. That is valid for electromagnetic energy moving between places of equal gravitational potential and would have applied to the experiments that Maxwell did. It is most likely valid as an assumption for a lot of other situations that experiments find themselves in and for the special theory of relativity. Where it should run into trouble is when you consider an electron as a twisted photon at different
Altitudes in the atmosphere and at different orbital energies around an atom. I seem to consider that the different states of an electron in terms of energy are different forms of the particle because it has absorbed or lost a photon to change its energy potential. Therefore it has a minutely different mass and energy. If it is translated in this operation then we find that the guage theory assumption does not hold under these conditions. So, when a photon or electron moves vertically in a gravitational field i.e. where the field energy is neither homogenous nor isotropic then the guage theory assumption does not hold.
Thanks for that Andy. I ought to do some more digging on this, but I’ve got a million and one other things to do. Note that I’ve said that a photon moving vertically doesn’t change its energy. For example, people usually say the ascending photon is redshifted, but Einstein said it’s emitted at a lower frequency at a lower elevation. So it doesn’t lose energy as it ascends. It had less energy to begin with than a photon emitted by the same process at a higher elevation. In similar vein people say the descending photon is blueshifted, but I say it doesn’t gain energy. Conservation of energy applies. It also applies when an electron falls down. The electron’s kinetic energy comes from its gravitational potential energy, which is mass-energy. Hence when you dissipate that kinetic energy, you’re left with a mass deficit. If that means gauge theory is wrong, great stuff. Thanks.
bonjour….merci…