If you’ve ever read Maxwell’s On Physical Lines of Force, you may have noticed this: “a motion of translation along an axis cannot produce a rotation about that axis unless it meets with some special mechanism, like that of a screw”. Maxwell was referring to what I can only describe as the screw nature of electromagnetism. If you have a pump-action screwdriver you’ll appreciate that linear force is converted into rotational force. That’s like an electric motor: current flows through the wire, and the motor turns. When you use an ordinary screwdriver, rotational force is converted into linear force, and the screw is driven into the wood. That’s like a dynamo: turn the rotor, and current flows. Hence the right-hand rule applies not just to electromagnetism, but to screw threads too:
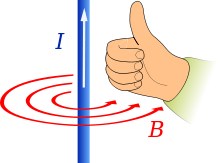GNUFDL right-hand rule image by Jfmelero see Wikipedia
In the Wikipedia right-hand rule article it’s called Ampère’s right hand screw rule. Other sources refer to Maxwell’s right hand grip rule. Some refer to the right handed cork screw rule and some even show you a picture of a screw:
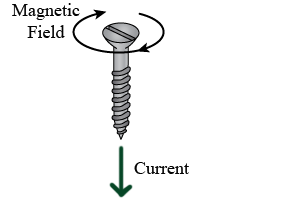Image by Kiran Daware, see electrical easy
Do a google search on corkscrew rule images. They are ubiquitous. So much so that the simplest demonstration of the translation-rotation principle is Michael Faraday’s homopolar motor of 1821. It featured a battery, a wire and a bath of mercury, but what do we see at the top of the Wikipedia homopolar motor article? A contemporary homopolar motor featuring a battery, a wire, a magnet, and a screw.
The electromagnetic field is not depicted
However when you read about the electromagnetic field in contemporary texts, the screw nature of electro-magnetism tends to be absent. And somewhat surprisingly, there are very few depictions of the electromagnetic field. You can see depictions of a gravitational field, depictions of a gravitomagnetic field, depictions of an electric field, and depictions of a magnetic field. But there are virtually no depictions of the electromagnetic field. What you see instead is pictures of electric fields and magnetic fields. You can find a few pictures that show both together, like figure 27-6 in the Feynman lectures. There’s also the anapole field in the 2013 Popular Mechanics article doughnut-shaped electromagnetic fields may explain dark matter:
Image credit: Michael Smeltzer/Vanderbilt
But pictures of the electromagnetic field are as rare as hen’s teeth. There’s a gap between the talk and the walk. You can read on Wikipedia that “over time, it was realized that the electric and magnetic fields are better thought of as two parts of a greater whole – the electromagnetic field”. You can also read what Oleg Jefimenko said: “neither Maxwell’s equations nor their solutions indicate an existence of causal links between electric and magnetic fields. Therefore, we must conclude that an electromagnetic field is a dual entity”. In addition you can read where John Jackson said “one should properly speak of the electromagnetic field Fμv rather than E or B separately”. But that’s in section 11. Not section 1. And people do speak of E and B separately, all the time. There’s an awful lot of places where you can read about the electric field and the magnetic field as if they’re two separate entities. And there’s virtually no places where you can see the electromagnetic field as the single entity it’s supposed to be. Sometimes it feels like Maxwell’s unification never happened.
You don’t create a magnetic field for the electron when you move
Sometimes it feels like Hermann Minkowski’s Space and Time never happened either. Towards the end, near figure 3, Minkowski said this: “In the description of the field caused by the electron itself, then it will appear that the division of the field into electric and magnetic forces is a relative one with respect to the time-axis assumed; the two forces considered together can most vividly be described by a certain analogy to the force-screw in mechanics; the analogy is, however, imperfect”. He was talking about the electron’s field. That’s an electromagnetic field. And he referred to electric and magnetic force. For charged particles, electric force is linear, whilst magnetic force is rotational. They’re related by a screw analogy, because of the screw nature of electromagnetism: a motion of translation along an axis cannot produce a rotation about that axis unless it meets with some special mechanism, like that of a screw. Because in ∇ × E = −∂B/∂t the equals sign is an “is”. The curl of E is the time-rate of change of B. But we don’t read about this. What we read instead that you create a magnetic field when you move a charged particle such as an electron. It just isn’t true. You know this, because you know that motion is relative. We could leave the electron exactly where it is and move you relative to it. However your motion doesn’t create a magnetic field for the electron. Because all along the electron had an electromagnetic field. Not an electric field, not a magnetic field, an electromagnetic field. You merely see a different aspect of that field when you move, that’s all. Because that field has a screw nature, and because it takes two to tango.
Electric field lines don’t work for charged particles
That means the depictions of a charged particle’s electric field are misleading. A positron doesn’t really have an outward pointing electric field. An electron doesn’t really have an inward pointing electric field:
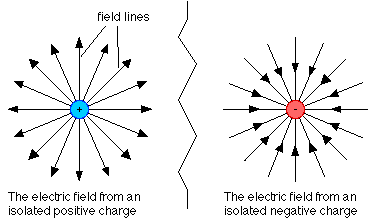Image by Andrew Duffy, see his PY106 course
Because each has an electromagnetic field. Yes, an electric field can be visualized on paper by drawing radial lines of force, or radial field lines if you prefer. But this visualization is not a good one for a charged particle. That’s because the force is not the same as the field. It results from electromagnetic field interactions, and it takes two to tango. An electron is not surrounded by a field of force. Nor is a positron. We only see a force when we set down a second electron, or a second positron. If we then have two positrons with no initial relative motion, they move apart linearly. We might then think that we could draw outward pointing arrowheads around each positron to represent the force pushing them apart. But if we have two electrons with no initial relative motion, they also move apart linearly too. For consistency we’d have to draw them with outward pointing arrowheads too. So the arrowheads just don’t work. Moreover they come with the mental baggage of sources and sinks. There is no outflowing from a positron. There is no inflowing for an electron, just as there is no inflowing Chicken Little waterfall of space for a gravitational field. All in all, electric field lines just don’t work for charged particles.
Magnetic field lines don’t work for charged particles
Magnetic field lines don’t work for charged particles either. They work for iron filings. You can shake them over a piece of paper and they line up like little compass needles. They mark out the field, and you can see plenty of images when you Google on magnetic lines of force. Some even show compass needles pointing along the lines of force. You are seeing something real, and something with pedigree that goes back to Faraday. He described them as physical in 1852, and those iron filings prove that there’s something physical there. Hence Maxwell wrote On Physical Lines of Force in 1861. But a charged particle doesn’t move along magnetic lines of force. An electron doesn’t scoot from the North pole of a bar magnet to the South pole. Instead it moves around the magnetic lines of force. Because of this you might say that they’re magnetic field lines as opposed to lines of magnetic force. That sounds reasonable, especially since an electron is said to have a magnetic dipole field rather like a bar magnet, and rather like a solenoid:
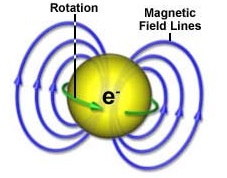Image from the national mag lab, see Magnets from Mini to Mighty and EMR
Only it isn’t enough. Because when you throw an electron through a solenoid, its path will trace out a clockwise helix. And when you throw a positron through a solenoid, its path will trace out an anticlockwise helix. That’s because the rotational magnetic force on a charged particle is orthogonal to the particle motion and to the magnetic field, as per the right hand rule. It also depends upon the charge. But when you throw a magnet through a solenoid, there is no helical path. Electrons and positrons move in opposite spirals in a bubble chamber, because of the magnetic field within it. But a magnet doesn’t spiral in a magnetic field. Magnetic field lines on their own are not enough. The motion of the electron or positron in a magnetic field is a product of the particle itself and the field. It takes two to tango. And it isn’t because the electron or positron has a magnetic field. The little magnet moves directly towards the big magnet, it doesn’t move around the magnetic field lines. The electron does, not because it has an electric field with field lines pointing inwards, not because it has a magnetic field with field lines going around and around, but because it has an electromagnetic field. It’s a combination of the electric field and the magnetic field, and you need to see it to understand it.
Combining electric and magnetic field lines
The electron’s electric field is said to be radial. That’s simple enough. However the electron’s magnetic field is said to be like that of a bar magnet, which isn’t. The bar magnet’s magnetic field is like that of a solenoid. The solenoid’s magnetic field is like that of a simple loop of wire. Let’s straighten out the wire to make it even simpler. Let’s consider the magnetic field around the current in the wire. That’s the simplest magnetic field I can think of, and it’s depicted as concentric circles. So, how do we combine the radial electric field lines with the concentric magnetic field lines? Let’s ask Maxwell. In 1871 he wrote a paper entitled Remarks on the Mathematical Classification of Physical Quantities. He said this: “Another distinction among physical vectors is founded on a different principle, and divides them into those which are defined with reference to translation and those which are defined with reference to rotation. The remarkable analogies between these two classes of vectors is well pointed out by Poinsôt in his treatise on the motion of a rigid body. But the most remarkable illustration of them is derived from the two different ways in which it is possible to contemplate the relation between electricity and magnetism”. There’s the translation and rotation again. Maxwell referred to Descartes, to Helmholtz and “his great paper on vortex motion”, and to Thomson and Tait. And to Ampère. Maxwell said this: “According to Ampère and all his followers, however, electric currents are regarded as a species of translation, and magnetic force as depending on rotation. I am constrained to agree with this view, because the electric current is associated with electrolysis, and other undoubted instances of translation, while magnetism is associated with the rotation of the plane of polarization of light, which, as Thomson has shown, involves actual motion of rotation”. This is the paper where he came up with convergence and curl and drew this picture:
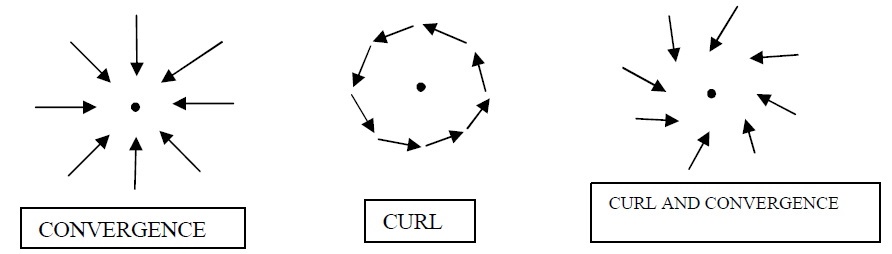Image by James Clerk Maxwell
It’s also where he said this: “It represents the direction and magnitude of the rotation of the subject matter carried by the vector σ. I have sought for a word which shall neither, like Rotation, Whirl, or Twirl, connote motion, nor, like Twist, indicate a helical or screw structure which is not of the nature of a vector at all. However it is in the nature of a vector field. The electric field has the convergence. The magnetic field has the curl. Curl is also known as rot, which is short for rotor. You can combine them to depict the electromagnetic field. Like this:
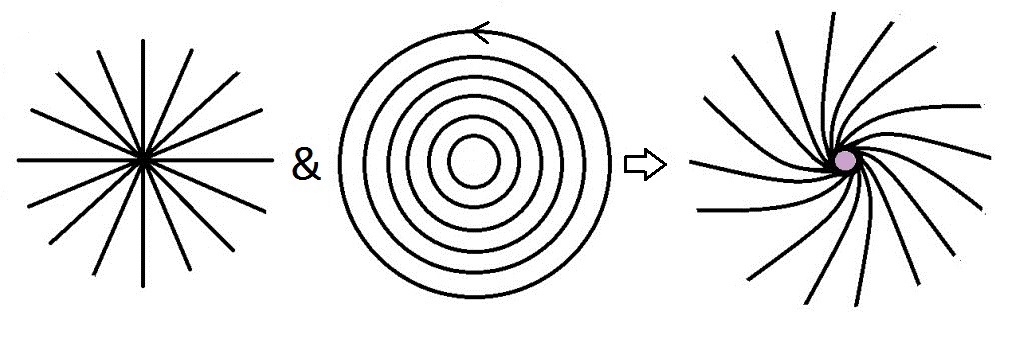Then you see the rotation, and the whirl, the twirl, and the screw structure. You see the screw structure of the “spinor”. The thing that’s responsible for the screw nature of electromagnetism. The thing that’s responsible for the way that charged particles move.
The linear electric force between charged particles
When you set down an electron and a positron such that they have no initial relative motion, they move directly towards one another. The force is linear, and we talk of Coulomb’s Law. That says the electrostatic force between two charged particles separated by a distance r is F = ke(q1q2) / r². The ke is Coulomb’s constant which is 1/4πε0, the 4π being related to a sphere and the ε0 being vacuum permittivity. The force is attractive if the charges q1 and q2 have opposite signs, and repulsive if they don’t. But why? These two charged particles aren’t throwing photons at one another. Or boomerangs. The virtual photons that are described as exchange particles are virtual. They aren’t real photons. They only exist in the mathematics of the model. Hydrogen atoms don’t twinkle, and nor does positronium, which is often described being like light hydrogen.
The rotational magnetic force between charged particles
Positronium is an “exotic atom” that doesn’t last long. It’s depicted as the electron and positron doing a little whirligig dance of death before annihilation:
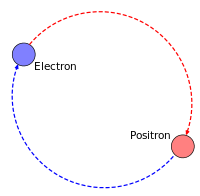CCASA image by Manticorp/Rubber Duck, see Wikipedia
The lifetime depends on the relative spin states. If the spins are antiparallel we have 11S0 singlet state para-positronium with a lifetime of 125 picoseconds, ending up as two 511keV photons. If the spins are parallel we have 13S1 triplet state ortho-positronium with a longer lifetime of about 142 nanoseconds, ending up as three gamma photons. There’s also 2S positronium with a lifetime of about a microsecond, ending up as five photons. See papers like Observation of positronium annihilation in the 2S state by D A Cook et al where they say it appears to survive collisions with the wall of the tube. All of this is salient reminder that the electron and the positron each has an electromagnetic field, not just an electric field. If you throw an electron through a solenoid it goes around and around. If you throw an electron past a positron, the particles go around and around each other as they close in. There’s obviously more than one way they can do it, and we could get into spherical harmonics or even toroidal harmonics. But to keep things simple we talk of the Biot-Savart Law, and then say the magnetic force vector between two charged particles is given as:
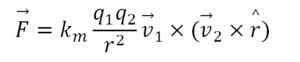
The km is the magnetic force constant which is μ0/4π, the 4π being related to a sphere and the μ0 being vacuum permeability. The v1 and v2 with the overhead arrows are the particle motion vectors, and the r with the hat is a unit vector in direction r. You can read about this on Frank Wolfs’ website. You can also read on Wikipedia that the Biot-Savart law is also used in aerodynamic theory to calculate the velocity induced by vortex lines. Note this: “In Maxwell’s 1861 paper ‘On Physical Lines of Force’, magnetic field strength H was directly equated with pure vorticity (spin), whereas B was a weighted vorticity that was weighted for the density of the vortex sea. Maxwell considered magnetic permeability μ to be a measure of the density of the vortex sea”. Maxwell didn’t quite get it right of course. He said this: “Let AB, Pl. V. fig. 2, represent a current of electricity in the direction from A to B. Let the large spaces above and below AB represent the vortices, and let the small circles separating the vortices represent the layers of particles placed between them, which in our hypothesis represent electricity”. His figure 2 is shown below. There’s a honeycomb of vortices, with particles between them. Perhaps there’s a later paper where he corrected this, but if Maxwell ever made a mistake, this is it:
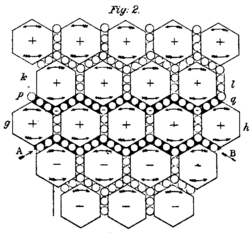Image by James Clerk Maxwell
There is no vortex sea. We don’t talk of spinors for nothing. A bispinor isn’t used to describe relativistic spin ½ wave functions for nothing. Because the vortices are the particles. On such the world turns.
Why charged particles move the way they do
So, why do the particles move linearly and rotationally? We refer to the Lorentz force law for this. The linear and/or rotational force on a particle of charge q is F = qE + qv Χ B, the v being velocity, and E and B being electric and magnetic fields respectively. Is this force present because charged particles are throwing photons at one another? No. Those photons are virtual, and virtual photons are not real. Is it because of some magical mysterious action at a distance? No. Even Newton knew that, over three hundred years ago. See his 1692 letter to Richard Bentley where he said this: “That gravity should be innate, inherent, and essential to matter, so that one body may act upon another at a distance, through a vacuum, without the mediation of anything else, by and through which their action and force may be conveyed from one to another, is to me so great an absurdity, that I believe no man who has in philosophical matters a competent faculty of thinking can ever fall into it”. He was talking about gravity as opposed to electromagnetism, but the same principle applies. I suspect Descartes knew that nearly four hundred years ago. I also suspect that if you’ve read Lorentz’s Nobel lecture you may have noticed that “this force is always due to the ether in the immediate vicinity of the electron”. Replace ether with space, and look to fluid dynamics which says counter-rotating vortices attract. Kelvin talked about this. If you know that, you will also know that co-rotating vortices repel. And that vortices swirl around one another too. Then you will know that the reason charged particles move the way they do is because of their spinor nature.
Cyclones and anti-cyclones
As per the Columbia heady collisions article, particles can be likened to tornadoes and hurricanes. You can liken the electron to a southern-hemisphere cyclone rotating clockwise. You can liken the positron to a northern-hemisphere cyclone rotating anticlockwise. In this analogy the positron isn’t like a meteorological anticyclone which rotates clockwise in the northern hemisphere, because that features central high pressure, not low pressure. But I’ll take the liberty of shortening anticlockwise cyclone to anti-cyclone. If you threw the cyclone past the anti-cyclone how would they move? A picture is worth a thousand words. An animation is worth ten thousand words, but for now a picture will have to do. Those two particles move towards each other, and around and around too:
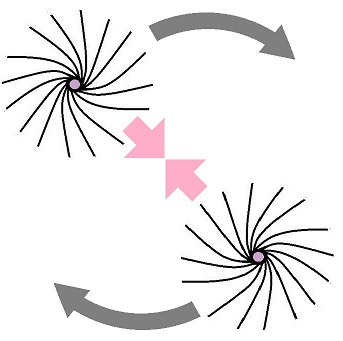
Why? Not because they’re slinging photons back and force. Not because of some magical mysterious action-at-distance. But because each is a dynamical spinor in frame-dragged space. A cyclone has intrinsic spin. So does an anti-cyclone. That’s what makes it what it is. Cancel one spin with the opposite spin, and all you’ve got is wind. An electron has intrinsic spin too. So does an anti-electron. That’s what makes it what it is. Cancel one spin with the opposite spin, and all you’ve got is light. It all makes sense.
Twist and turn
Something else that makes sense is that a charged particle doesn’t have an electric field, or a magnetic field. It has an electromagnetic field. Because it’s an electromagnetic wave going around and around, and there’s only one wave there. The result of this is a standing-wave standing-field dynamical chiral spinor called an electron or a positron. The end product is not altogether unlike the “twisted space” gravitomagnetic field, but with no solid central body. It’s a wave going round and round, not a planet, not a football, and not a point particle. There is no central billiard ball, that thing in the middle is like the eye of the storm:
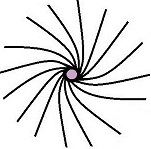
The state of space where a gravitational field is, is inhomogeneous. The state of space where a photon is, is curved. It’s curved one way, then the other. The state of space where an electron is, is curved, all the same way, all the way round. The state of space where a positron is, is curved, all the same way, all the way round, but the other way round. Only it isn’t just curved in two dimensions, it’s curved in three dimensions. It’s curled, it’s twisted. In a way the electron is a twistor, and its electromagnetic field is twistor space. It’s not like Penrose suggested, but it’s not far off. You could say the electron electromagnetic field is a twist field. Look at the picture above. Hold your arms out wide and imagine you’re an aeroplane. Imagine you could fly forward into this twisted space. Imagine what would happen: your wings would tilt, they would turn clockwise with the twist. The twist results in a turn. Only if you weren’t moving, if the electron was moving relative to you, you might think you were in a turn field, not a twist field. That’s what the screw nature of electromagnetism is all about. Twist and turn.
The electromagnetic field is a twist field
That’s why the electromagnetic field is a dual entity and the greater whole. Because it’s a twist field, and when you move through it, you turn. That’s why a charged particle has an electromagnetic field rather than an electric field or a magnetic field. Because it’s an electromagnetic wave going around and around, and there’s only one wave there. You cannot remove the electric aspect of the electromagnetic wave, because it’s merely the spatial derivative of potential. Nor can you remove the magnetic aspect of the electromagnetic wave, because it’s merely the time derivative of potential. Nor can you do either when the wave is going round and round in the guise of a spin ½ standing wave. In this respect the phrase electric charge is a misnomer. The charged particle has an electromagnetic field, so we ought to call it electromagnetic charge. Yes, we can contrive an ensemble of charged particles so that some aspect of their electromagnetic fields are counter-balanced and so masked. Then when we observe other charged particles, we sometimes see the linear force only, and we sometimes only the rotational force only. When we only see the linear force we talk of an electric field, when we only see the rotational force we talk of a magnetic field. To understand how this works, we have to understand how a magnet works. For some strange reason Feynman couldn’t explain it. Richard Feynman, the great explainer, couldn’t explain how a magnet works. He didn’t understand it. But amazingly, in 1820, André-Marie Ampère did.
PS: I’ve been deluged with robotized medical spam so I’ll have to tighten up on the comments. Apologies for any inconvenience. Please try to avoid pharmaceutical-like words.
John, what do you think about the supposedly new discoveries of angular light screw vortexes that I read about on Physics.org ? According to your articles of the screw nature of electromagnetism, Maxwell and the more recent scientist making light knots among others, allready stated these light vortexes to be possible ?
They don’t seem to be anything new, Greg. See tying light in knots featuring Mark Dennis and others, and see Miles Padgett’s Glasgow website:
I know that Emilio Pisanty, a co-author of one of the recent papers knows about Mark Dennis. See this. But there’s no mention of Dennis in the references in https://arxiv.org/abs/1901.10942. Miles Padgett get a few mentions.
Thank for the clarifications and new links John.
Thanks for this article. Lots of insight and ideas for what electrons might be.
My pleasure Tom. I think it’s fairly cut and dried that the electron is a self-trapped 511keV photon in a chiral double-loop trivial-knot configuration. Do play around with sinusoidal paper strips making Moebius strips as per
” rel=”nofollow ugc”>this picture. Also see https://physicsdetective.com/articles/ and https://physicsdetective.com/the-electron/.
Can we assume that each field line is a turning screw? The right hand rule gives the direction of the linear force?
No, Johnny. Those field lines don’t exist.
.
PS: I remember this:
.
http://johnyjagannath.blogspot.com/2020/07/michelle-jenneke-guy-sneaks-on-track.html
.
Brill!
John Duffield aka “Farsight” wrote above :
.
” You can see depictions of a gravitational field, depictions of a gravitomagnetic field, depictions of an electric field, and depictions of a magnetic field. But there are virtually no depictions of the electromagnetic field. What you see instead is pictures of electric fields and magnetic fields. You can find a few pictures that show both together, like figure 27-6 in the Feynman lectures. ”
.
John, the simple explanation why there are no depictions of the electromagnetic field is that there simply is no such thing as an electromagnetic field.
But only the omniscient Wikipedia knows better !! :-))
.
” over time, it was realized that the electric and magnetic fields are better thought of as two parts of a greater whole – the electromagnetic field ”.
.
Let’s re-phrase it slightly : electric and magnetic fields are better thought of as two inseparable parts of one greater whole – electromagnetism.
.
NOW COMES VERY IMPORTANT INFO
.
” There’s also the anapole field in the 2013 Popular Mechanics article doughnut-shaped electromagnetic fields may explain dark matter. ”
.
“Popular Mechanics” magazine is not even “Popular Physics” magazine, so like some uneducated Wikipedia volunteer editor, they imagine non-existent electromagnetic fields. BUT, what they reported as the doughnut-shaped electromagnetic field called an anapole is in reality much more than doughnut-shaped, and instead of being some non-existent electromagnetic field, is in fact AN ELECTROMAGNETIC WAVE. So, it was close.
.
Yes, it is a self-enclosed electromagnetic WAVE that from afar would look like a particle, and if you want to learn more details about it, you are welcome to read this page :
.
https://quantumantigravity.wordpress.com/hopfotrino/
.
Fascinating views Zbigniew, what you just described as an electromagnetic screwtwist wave/field is basically what John has been preaching about electromagnetism itself and for the overall design of the electron torus and photon as well !
What are your thoughts on what job(s) neutrinos perform in the nucleus before being expelled due to the decay process ? My crude hypothesis is that they act as ball bearings/ bushings instead of there being quarks involved.
Greg R. Leslie wrote above :
.
” Fascinating views Zbigniew, what you just described as an electromagnetic screw-twist wave/field is basically what John has been preaching about electromagnetism itself and for the overall design of the electron torus and photon as well ! ”
.
Dear Greg, thank you so very much for your kind reply, because ….
.
SUB-QUANTUM KNOT-WAVE MECHANICS was born today :
.
https://quantumantigravity.wordpress.com/sqkwm/
.
Greg, I have not looked into neutrinos well enough to have an opinion.
.
I am very glad to hear about John’s area of interest, and I am looking forward to our discussion.
.
The Popular Mechanics article that John found about the “anapol particle” :
.
https://news.vanderbilt.edu/2013/06/10/dark-matter/
.
in combination with the “hopfotrino particle” :
.
https://quantumantigravity.wordpress.com/hopfotrino/
.
will open up for us an opportunity to develop John’s intuitions into actual mainstream details, because the Devil is in the details, as always. :-))
.
” An electromagnetic anapole is the only allowed electromagnetic form factor for Majorana fermions. ”
.
The “anapol particle” and the “hopfotrino particle” are two variations of the same kind, and this indicates possibility of more such variations, especially for the electron.
.
If you look at the anapole :
.
.
it is composed of two fields: electric (red) and magnetic (blue), so this makes it an electromagnetic particle.
.
And what quantum particles are equivalent of ??
.
Subatomic particles are equivalent of waves of a field.
.
Therefore, the anapole particles is NOT an electromagnetic field. Anapol PARTICLE is an electromagnetic wave of the ELECTRIC FIELD.
.
And this is how the sub-quantum hopfotrino particle looks like :
.
.
Ziggy: a lot of the things you read about on this website are not my intuitions. They belong to people like John Williamson and Martin van der Mark, and Qiu Hong Hu, and a whole lot of other guys. What astonishes me is just how great material is out there, going unreported.
.
Like you said in your email, let’s talk about all this stuff offline.
.
I love physics!
I still don’t get, from an outsider perspective, if electric fields and magnetic fields are just the two components of the “real” electromagnetic field, or if they can exists as pure fields by themselves.
I’m aware of Jefimenko’s work, I can’t understand it due to my math limitations, but he also always repeated that the electromagnetic field is one and alone by itself and neither magnetic or electric fields induce or have a causal relationship to each other.
Well, so?
As usual the most simple questions arise (always from an outsider perspective): why do permanent magnets and (don’t forget them!) electrets exist? They are quite real and tangible, one can buy magnets quite easily and play with them, and with a little more difficulty one can buy also electrets. Where is the electromagnetic field in those “objects”?
Davide, to answer your question:
.
I still don’t get, from an outsider perspective, if electric fields and magnetic fields are just the two components of the “real” electromagnetic field, or if they can exists as pure fields by themselves.
.
They can exist by themselves, but not as “pure” fields.
.
I’m aware of Jefimenko’s work, I can’t understand it due to my math limitations, but he also always repeated that the electromagnetic field is one and alone by itself and neither magnetic or electric fields induce or have a causal relationship to each other. Well, so?
.
That’s right. When you move relative to the thing that you call an electric field, you start to notice that it’s starts to look like a magnetic field too. Because the electric field isn’t a pure field. Nor is a magnetic field.
.
As usual the most simple questions arise (always from an outsider perspective): why do permanent magnets and (don’t forget them!) electrets exist? They are quite real and tangible, one can buy magnets quite easily and play with them, and with a little more difficulty one can buy also electrets. Where is the electromagnetic field in those “objects”?
.
It’s somewhat hidden. Imagine you set down an electron in a location where a positron was present, and the positron was somehow fixed. The electron would move linearly around the positron, and rotationally around it. It would spiral towards it. The thing to note is this: electromagnetic field interactions result in linear and rotational force.
.
When you set your electron down in a location where a whole host of charged particles are present, then if the electron only moves linearly, you would say an electric field was present. That’s because the arrangement of your charged particles is such that equal and opposite rotational forces balance, but the linear forces do not. If however you threw the electron through this location, you would notice that it also exhibited rotational motion. That’s because the rotational forces are not balanced for a moving electron.
.
When you set your electron down in a location where a whole host of charged particles are present, then if the electron only moves rotationally, you would say a uniform magnetic field was present. That’s because the arrangement of your charged particles is such that equal and opposite linear forces balance, but the rotational forces do not. If however you threw the electron through this location, you would notice that it also exhibited linear motion. That’s because the linear forces are not balanced for a moving electron.
.
There is no way to contrive your charged particles such that all your test particles only undergo linear motion, or only undergo rotational motion.
.
Note that an electromagnetic field is not a field of force per se. Nor is an electric field, and nor is a magnetic field. The electron moves the way that it does because it’s a “dynamical spinor”. The electron goes round in circles in a uniform magnetic field because it undergoes Larmor precession. This is somewhat similar to the gyroscopic precession of a boomerang. The is no external force pushing the electron round and round in circles. The electron drives itself around in circles. So does the positron, but it goes round the other way, somewhat like a left-handed boomerang goes round the other way. The fact that the electron goes round one way and the positron goes round the other way, tells you that the magnetic field is not a field of force. It’s similar for the electric field, where the electron moves linearly one way and the positron moves linearly the other.
Thanks for your kind reply, I reserve myself to read again and think about your reply. I just add another question: since I somewhat agree to your view here (I’m an outsider in physics, I’m just passionate about it and I’m trying to catch up with laws and math at age of 40. Unfortunately I discovered my true love very late in life), and since I also read other people’s work where they were trying to tell to the reader the fact that electromagnetism is a dual phenomeon and that, for example, as a consequence a capacitor is not a static electric field container, and the same is for an inductor with regards to the magnetic field. And so also permanent magnets must have circular currents etc etc.
In Italy they still teach that a changing electric field induces a magnetic field to explain EM waves and the meaning of Maxwell’s equations, while, instead, Jefimenko was clear: they do not do this. I found also that Einstein was mislead by this concept. I suspect that a causal relationship, as that thaught in schools, poisons any possibility to true understanding.
Well, the questions is: can you tell me if this knowledge you published in this series of articles is common knowledge or is it somewhat neglected and underrated?
Because I had to search hard to connect dots in those years passed reading online articles, and still I don’t get if current mainstream physics is doomed to inability to understand. The fact that Feynman eluded the answer to how a magnet works is the proof.
So, what are you discussing in your articles, is lost knowledge? That needs to be taken more seriously again? Are these concepts you depicted in this series of articles, also inside physics books? Thanks for you elucidations and sorry for me being so pedant.
Davide, sorry, this post was in the spam folder for some reason. I see that you repeated it.
Thanks for your kind reply, I reserve myself to read again and think about it. I just add another question: since I agree to your view here (I’m an outsider in physics, I’m just passionate about it and I’m trying to catch up with laws and math at age of 40. Unfortunately I discovered my true love very late in life). I also read other people’s work where they are struggling trying to tell the reader the fact that electromagnetism is a dual-but-one phenomeon and that, for example, as a consequence, a capacitor is not a static electric field container (it has also magnetic field canceled out), and the same is for an inductor with regards to the magnetic field, and so also permanent magnets must have circular currents etc etc.
In Italy they still teach that a changing electric field induces a magnetic field (and so on..) to explain EM waves and the meaning of Maxwell’s equations, while, instead, Jefimenko was clear: they do not do this. I found also that Einstein was mislead by this concept. I suspect that a causal relationship, as that thaught in schools and perpetrated in many books, poisons any possibility to true understanding.
Well, the questions is: can you tell me if this knowledge you published in this series of articles, is common knowledge or is it somewhat neglected and underrated?
Because I had to search hard to find this analogies between different authors and connect dots in those years passed reading online articles, and still I don’t get if current mainstream physics is doomed to inability to understand. The fact that Feynman eluded the answer to how a magnet works is the proof.
So, what are you discussing in your articles, is “lost” knowledge? A knowledge that needs to be taken more seriously again? Are these concepts you depicted in this series of articles, also inside physics books?
Thanks for you elucidations and sorry for me being so pedant.
Thanks for your kind reply, I reserve myself to read again and think about it. I just add another question: since I agree to your view here (I’m an outsider in physics, I’m just passionate about it and I’m trying to catch up with laws and math at age of 40.
.
My pleasure Davide. I hope this website helps.
.
Unfortunately I discovered my true love very late in life). I also read other people’s work where they are struggling trying to tell the reader the fact that electromagnetism is a dual-but-one phenomenon and that, for example, as a consequence, a capacitor is not a static electric field container (it has also magnetic field cancelled out), and the same is for an inductor with regards to the magnetic field, and so also permanent magnets must have circular currents etc etc.
.
I’d be interested to see such work. I think electromagnetism is badly taught. It sometimes feels as if Maxwell’s electromagnetic unification never happened.
.
In Italy they still teach that a changing electric field induces a magnetic field (and so on..) to explain EM waves and the meaning of Maxwell’s equations
.
They do that in other countries too.
.
Jefimenko was clear: they do not do this.
.
That’s right. A changing electric does not create a magnetic field, a changing electric field IS a magnetic field.
.
I found also that Einstein was misled by this concept. I suspect that a causal relationship, as that taught in schools and perpetrated in many books, poisons any possibility to true understanding.
.
I agree. Einstein had a picture of Maxwell on his study wall. See https://www.theguardian.com/science/2015/dec/08/einstein-inspired-by-james-clerk-maxwell, where you can read this: “When Einstein was asked if he stood on the shoulders of Newton, he replied “No, on the shoulders of Maxwell”.” However, I don’t think Einstein actually read all of Maxwell’s work.
.
Well, the questions is: can you tell me if this knowledge you published in this series of articles, is common knowledge or is it somewhat neglected and underrated?
.
It is not common knowledge, it is somewhat neglected. If you were to ask a professional physicist about the screw nature of electromagnetism, quoting Maxwell as per the first paragraph of this article, or quoting Minkowski as per the third paragraph, I imagine the reply would be dismissive. Perhaps you could try asking some professional physicists about that.
.
Because I had to search hard to find this analogies between different authors and connect dots in those years passed reading online articles, and still I don’t get if current mainstream physics is doomed to inability to understand. The fact that Feynman eluded the answer to how a magnet works is the proof.
.
I think mainstream physics refuses to understand, because it does not want to admit that mainstream physics is in any way flawed. See the beginning of the next article https://physicsdetective.com/how-a-magnet-works/, where I start by saying “There’s a rather interesting article called Three Words That Could Overthrow Physics: What is magnetism?”. The Standard Model does not explain magnetism. This is a glaring omission that some professional physics do not want to admit.
.
So, what are you discussing in your articles, is “lost” knowledge?
.
Yes. For example Einstein said the speed of light varies with gravitational potential, and that this is why the horizontal light beam curves downwards. However you will not find that in modern texts. Moreover if you talk about this on some physics forums, you may find that you are banned.
.
A knowledge that needs to be taken more seriously again?
.
Yes.
.
Are these concepts you depicted in this series of articles, also inside physics books?
.
Some of them are inside older physics books. Most of them can be found in older papers. For example, Schrodinger spoke of an electron as a wave in a closed path. See paragraph 2 of page 26 here: http://hermes.ffn.ub.es/luisnavarro/nuevo_maletin/Schrodinger_1926_Quantisation_II.pdf). However you won’t find that in a modern physics book.
.
Thanks for you elucidations and sorry for me being so pedant.
.
There is no need to apologise. It is good to talk physics. It is my love too.
Perfect. It’s exactly what I wanted to hear.
Every reply to quoted parts by you, meets the expectations I was searching for. Your content really helped me to match the suspects I was having.
I don’t know if you know about Ivor Catt, it’s another author I’m reading about, he is 87 but still alive in UK. He wrote many books, the first of them is this one:
http://forrestbishop.mysite.com/EMTV1/Electromagnetic%20Theory%20Ivor%20Catt%20Vol%201%20searchable.pdf
Try reading it, there are many others by the trio Catt – Davidson – Walton, and there is also Ivor Catt’s big mess website still online. To make the long story short, he is struggling since 1967 to try to tell IEEE and the scientific community that EM theory is flawed in multiple parts and that the solution to this lies in…… read about it yourself if you have the time. Obviously the outcome of their claims is derision and suppression, althought in the eighties and nineties they got much attention, it appears, on the pages of World Wireless magazine, ending completely silenced some time after.
(I’m in touch with them by mail and I often hear also Forrest Bishop and others in that circulation.)
You can also see Malcolm Davidson recent video on the subject:
https://www.youtube.com/watch?v=2_PNNdri8I4&ab_channel=MalcolmDavidson
Please remember they are mainly engineers and not purely physicists. Now they don’t cowork anymore but they remained still on their claims up to today. I find their claims to match your observations, and in this respect I’m also doing a detective job to connect different author’s claims.
About the fact that one has to read original Treatises and older books to reach right contents, while it seems modern books are weaker in this respect, is another truth that I found quite strange to digest at first. But it’s real and you confirmed also this.
“Oh My gosh” goes to current students and younger people: I really don’t get how they will understand something in this situation.
Thanks again for your help, I will delve more on your contents trying to perfect my knowledge.
Davide: I watched the Malcolm Davidson video. I think he’s generally correct, but at 6 minutes 59 seconds I wondered what he knows about displacement current, which is in essence light. See https://physicsdetective.com/quantum-computing-and-the-quantum-quacks/ where I talk about Nader Engheta. He featured in the 2010 physicsworld article “Taming Light at the Nanoscale”. The article concerns optical circuitry, and includes this: “But is the motion of charged particles the only current we have available? Those with a good memory for Maxwell’s equations of electromagnetism will remember that in addition to the familiar electric field, E, there is also a displacement field, D”. I’m not sure if Malcolm knows about the Poynting vector inherent in light, see
which I show in https://physicsdetective.com/the-electron/. He mentioned the Poynting vector in a transmission line at 10:15 so he probably knows indirectly. Especially since at 14:26 he says a length of space separating two points A & B can be modelled as a transmission line. I talk about this in https://physicsdetective.com/the-toe-that-maxwell-missed/: “It’s like light is an alternating current in a lossless transmission line of its own making”. Perhaps Malcolm is lacking the concept that an electron is displacement current in a twisted double loop, and that conduction current is therefore not the fundamental current of electromagnetism. I was a little disappointed at 15:52 to hear him talking about E and H as if they’re two separate things, and to hear him being somewhat dismissive of displacement current at 16:41. However he does refer to it on researchgate, so maybe I’m being unfair. Perhaps I’m also being unfair by saying there was a bit of an omission at 27:49 re power transmission, which is done via AC rather than DC. But it was good to see him giving some Heaviside history at 23:07. I was also pleased to hear him say light waves are TEM waves at 28:10, and that they are fundamental. I think Malcolm would be pleased to read about William Kingdon Clifford’s space theory of matter dating from 1870.
.
Edit: I took a look at Ivor Catt’s website. It’s a rather chaotic and confrontational. I found it difficult to find any physics I could comment upon. I thought his book was more reader-friendly. I liked how he talked about unification on page 28, and says there’s no causal relationship between E and H in an electromagnetic wave. However he thinks E and H are at literal right angles, and doesn’t know that E is the spatial derivative and H is the time derivative of one wave. Minskowski talked about this when he referred to the time axis in Space and Time. I was unhappy that there was no mention of the word screw in the book. But I liked the talk of displacement current, and thought the depiction of a capacitor as a transmission line on page 70 was good. I have to go out now. I will look at this further tomorrow.
Hi John,
I can confirm strongly that Catt+Davidson believe that E and H can’t exists by their own but are one thing alone, the TEM, or “Heaviside Signal”. They dismiss displacement current at all. Catt in particular did publish a sensationalistic article that was heavily criticised, “Displacement current (and how to get rid of it)” where they demostrated that displacement current does.. not exist, because a capacitor is a transmission line (they proceeded with a demostration and relative math).
Catt goes a little deeper and some time after, proclaimed that “current in wires is the last of the medieval fluids: it does not exists”. So if you are willing to delve in that mess of publications, you will soon find that those engineers sticked on these claims for all their lives, and still today: the current in the wires is only a loss, and the real thing is the TEM in the dielectric adjacent the wires. The “Primitive” is the TEM wave, and the Poynting Vector has physical reality, it’s not just ExH. They call it “energy current” and can only travel at the speed of light. The main article is “the Death of Electric Current”.
So they see the electron current in wires as a mere loss, it’s not the circulation of electrons, as in “electron drift”, that causes a magnetic field around the wire. The magnetic field was already there with the E field travelling outside the wires, and the penetration inside an imperfect conductor, which is the wire, is the cause of “electron drift”, or in other words “common conduction current”. It is useful just to compute the energy, but it is not the primary cause, it’s an effect.
See more here, from Forrest Bishop, a follower of Catt: http://www.naturalphilosophy.org/pdf/abstracts/abstracts_paperlink_7395.pdf
(You noticed mentions of Heaviside because their work is heavily based on Oliver’s findings.)
You won’t find “screw” or “twisting” or any circular movement descriptive word by Catt becuase (I noticed) he dismiss every “vorticular” characterization in everything, and in EM theory in particular.
As you see, if you are an outsider like me, you will soon end in a world of science where there are many other researchers, some of them write down things, like you do in your website, like those above did in magazines and publications, but the outsider can only read, try to understand and compare.
The outsider can’t tell who is right and who not. The outsider can only get feelings of what can be really right, and what not. Little by little, one day the outsider can reach a level where he can also write down something for the future readers.
But that mainstream science is in good form, that, nobody believes anymore.
That’s it. Hope to exchange something more when I’ll be more “educated”.
Davide:
.
I can confirm strongly that Catt+Davidson believe that E and H can’t exists by their own but are one thing alone, the TEM, or “Heaviside Signal”. They dismiss displacement current at all. Catt in particular did publish a sensationalistic article that was heavily criticised, “Displacement current (and how to get rid of it)” where they demonstrated that displacement current does.. not exist, because a capacitor is a transmission line (they proceeded with a demonstration and relative math).
.
I share their view on this, but instead of calling it a TEM, I just call it light, and I think of displacement current as an innate characteristic of light. In addition, I think there is a real physical displacement of space associated with light. I think of them as two aspects of the same thing. I don’t know if you’ve read Taming light at the nanoscale yet, but it’s well worth it. Taming light is taming displacement current.
.
Catt goes a little deeper and some time after, proclaimed that “current in wires is the last of the medieval fluids: it does not exists”.
.
Trust me, it exists in a lightning bolt. And in my DC welder. And in a cathode ray tube.
.
So if you are willing to delve in that mess of publications, you will soon find that those engineers sticked on these claims for all their lives, and still today: the current in the wires is only a loss, and the real thing is the TEM in the dielectric adjacent the wires.
.
I think that’s true of a transmission line.
.
The “Primitive” is the TEM wave, and the Poynting Vector has physical reality, it’s not just ExH. They call it “energy current” and can only travel at the speed of light.
.
I agree with that, but I just call it light.
.
The main article is “the Death of Electric Current”.
.
I read it: http://www.ivorcatt.com/2608.htm . I think Catt goes too far. Perhaps because he doesn’t know that the electron is a double twisted loop of his TEM. See the bottom of page 2 where he says “Any apparently steady field is a combination of two energy currents travelling in opposite directions at the speed of light. That isn’t true of the electron. The energy current is travelling in the same direction round and round, but with a Mobius twist.
.
So they see the electron current in wires as a mere loss, it’s not the circulation of electrons, as in “electron drift”, that causes a magnetic field around the wire. The magnetic field was already there with the E field travelling outside the wires, and the penetration inside an imperfect conductor, which is the wire, is the cause of “electron drift”, or in other words “common conduction current”. It is useful just to compute the energy, but it is not the primary cause, it’s an effect.
.
Noted. I think they’re generally right here, in that electrons in a wire move very slowly. But the field that’s already there is the electromagnetic field.
.
See more here, from Forrest Bishop, a follower of Catt: http://www.naturalphilosophy.org/pdf/abstracts/abstracts_paperlink_7395.pdf
.
I read it. I do not like i=qc because anything associated with charge cannot move at the speed of light c. I note the mention of a Mobius twist on page 13. I do wish these guys had an electron model. Then they would understand charge, and know that the electric circuit and the transmission line was made of electrons and protons and nothing else. These charged particles are their TEM waves wrapped up into a closed path. That’s all that exists. The only way to make a linear TEM wave in a transmission line is to move a charged particle.
.
(You noticed mentions of Heaviside because their work is heavily based on Oliver’s findings.)
.
Noted. You will hear complaints from me saying Maxwell’s equations are Heaviside’s equations, and expressing unhappiness that some of Maxwell’s knowledge was lost.
.
You won’t find “screw” or “twisting” or any circular movement descriptive word by Catt because (I noticed) he dismiss every “vorticular” characterization in everything, and in EM theory in particular.
.
That’s sad, because this is important in understanding why charged particles attract and repel, and how linear electric force is converted into rotational magnetic force and vice versa.
.
As you see, if you are an outsider like me, you will soon end in a world of science where there are many other researchers, some of them write down things, like you do in your website, like those above did in magazines and publications, but the outsider can only read, try to understand and compare. The outsider can’t tell who is right and who not. The outsider can only get feelings of what can be really right, and what not. Little by little, one day the outsider can reach a level where he can also write down something for the future readers.
.
Start by understanding the photon, then how pair production works, then the electron. These are the fundamentals. You cannot understand electromagnetism without this. Start here, https://physicsdetective.com/what-is-a-photon/ . When you’ve finished each article, click on NEXT at the bottom.
.
But that mainstream science is in good form, that, nobody believes anymore. That’s it. Hope to exchange something more when I’ll be more “educated”.
.
Nice talking to you, Davide.
Does an em wave have extent? Like a water wave has a peak to trough distance?
Yes and no. See the photon. Plank’s constant of action h applies to all photons, which have energy E=hf. The dimensionality of action can be expressed as momentum x distance, and I think that there’s a distance that’s common to all photons. I think it’s a real distance, and that all photons have the same amplitude. See how pair production works. I think this amplitude is 3.86 x 10ˉ¹³ metres. However that isn’t the extent of the photon, just as the wave height isn’t the extent of an ocean wave. The ocean wave extends deep into the ocean, far below the surface, with no real cutoff. See the gif below. At some depth it won’t be detectable any more because of “noise”. And for a wave in space, there is no surface.
.
Thank you!
.
Found a broken link in “photon”
http://www.rain.org/~karpeles/einsteindis.html
Fixed. Link rot is the bane of my life. As is the whack-a-mole war against Sci-Hub.
https://www.earth.com/news/lightning-sparks-the-discovery-of-a-new-electromagnetic-wave/
This article of John’s seems the best place to park this article for everyone’s scientific curiosity. The headlines of said article are very misleading, but it’s still a nice, tidy read.
https://www.google.com/search?q=jethro+tull+the+whistler+lyrics&ie=UTF-8&oe=UTF-8&hl=en-us&client=safari&si=ACC90nzcg09uT9dLCxMVYtMO0-0pjgQ_JR12fuxEIIyv63Ip94qTV1AYapsQRC_0ZtNEAZrbCZ2pM-pdXv1WPwgP14hjAXt-S9vRLPXKTmBdrXjzGtZli0OKG2T205r_Iu2ySi2vysiy4m_qc4v65xRkI8Qz9uSCPi4KrOgcIuSi6A6AzLIjGKM%3D&ictx=1&ved=2ahUKEwikl-qOpIaIAxUmtokEHVrVF28QjukCegQIORAC
Steve, The Son of Anders named Ian & Cohorts are one of my top 5 bands. With that song itself being in my top 5 Tull songs !
Uh huh: https://en.wikipedia.org/wiki/Whistler_(radio) : A whistler is a very low frequency (VLF) electromagnetic (radio) wave generated by lightning.[1] Frequencies of terrestrial whistlers are 1 kHz to 30 kHz, with maximum frequencies usually at 3 kHz to 5 kHz. Although they are electromagnetic waves, they occur at audio frequencies, and can be converted to audio using a suitable receiver. So a “specularly reflected whistler” isn’t a new type of electromagnetic wave in the fundamental sense that I was thinking.
LOL ! I was obviously duped again by a headline, shame on me !
I actually went to Wikipedia and read up, first on lightning. Which lead me to the triboelectric effect. And then onto tornados and thunderstorms in general and numerous other sublinks. Everything except for the subject matter of whistlers themselves !
But the most important thing for me is : that the correct scientific facts are presented. And as a teacher and professional journalist you excelle at both, Boss.
No problem Greg. I think it’s good science anyway, even though it’s not the fundamental physics I was anticipating.