The neutrino

The neutrino was proposed by Wolfgang Pauli in 1930 to account for the conservation of energy and spin angular momentum in beta decay. You can find his original letter to Lise Meitner and others on the Fermilab MicroBooNE database, along with the English translation:

Pauli later said “I have done a terrible thing. I have postulated a particle that cannot be detected”. He was wrong about that. He was wrong about some other things too. He talked about a particle that travels slower than light, and he called it a neutron. This was the name given to the neutron proper by James Chadwick in 1932. Hence the name was changed from neutron to neutrino by Edoardo Amaldi and Enrico Fermi. They were Italian. Amaldi was joking, but Fermi wasn’t, and the name stuck. He came up with a paper on beta decay in 1933 which Nature rejected, see the English translation at MicroBooNE prefaced by Fred Wilson. Because of that rejection, Fermi took a break from theoretical physics and did some experimental physics. That’s why he became “the architect of the nuclear age”. That’s why it’s Fermi’s interaction. Electrons are called fermions because of Fermi. We have Fermilab because of Fermi. We have slow neutrons because of Fermi.

Free neutron decay

Talking of which, perhaps the cleanest example of beta decay is free neutron decay. Outside of a nucleus the neutron decays in about 15 minutes into a proton, an electron, and an antineutrino: n → p + e^– + v̄_e. That’s an antineutrino rather than a neutrino, but no matter. Some part of the neutron suffers some kind of partial annihilation, resulting in an electron and its half-brother the antineutrino. In circa four cases per million the proton and electron remain bound as a hydrogen atom, because the electron had very little kinetic energy. However most of the time the electron is emitted as a fast-moving beta particle:

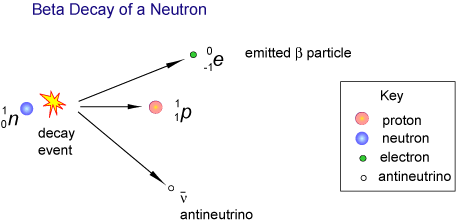Beta decay image from CSIRO, see The Sun: Energy from Nuclei

The electron kinetic energy varies in a smooth continuous fashion, such that there’s a “spectrum” of electron kinetic energies. See the Wikipedia beta decay article which talks about early work by Lise Meitner and Otto Hahn in 1911, and by Jean Danysz in 1913. It says: “these measurements offered the first hint that beta particles have a continuous spectrum”. It goes on to say that in 1914 James Chadwick made more accurate measurements which showed that the spectrum was continuous, and that in 1933 Charles Ellis and Nevill Mott demonstrated that the beta spectrum has an upper bound. See Rod Nave’s hyperphysics for a picture:

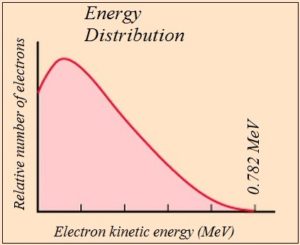Image from Rod Nave’s hyperphysics

The upper bound is the decay energy. We start with a neutron with a mass-energy of 939.565MeV. It spits out an electron and an antineutrino and becomes a proton with a mass-energy of 938.272MeV. The difference is 1.293MeV, and the proton gets so little kinetic energy that we can ignore it. So subtract the electron mass-energy of 0.511MeV from the 1.293MeV, and we’re left with the decay energy of 0.782MeV. The books always balance, energy is always conserved. So when the electron is emitted with hardly any kinetic energy, circa 0.782MeV departs in the guise of an antineutrino. When the electron is emitted with kinetic energy of 0.2MeV, circa 0.582MeV departs in the guise of an antineutrino. When the electron is emitted with kinetic energy as close to 0.782MeV as we can measure, hardly any energy departs in the guise of an antineutrino.

Spin statistics

The books also balance when it comes to spin. This is to do with the spin statistics theorem which is related to the Pauli exclusion principle. See John Baez’s spin, statistics, CPT and all that jazz. He says bosons change phase by +1 when you rotate one by 360° or switch two of them, whilst fermions change phase by -1. He also talks about topological solitons, and twist, and detectives. Interesting stuff. What’s also interesting is that the Einstein-de Haas effect demonstrates that spin angular momentum “is indeed of the same nature as the angular momentum of rotating bodies as conceived in classical mechanics”. Something else that’s interesting is that an overstressed flywheel can break apart with pieces flying off in different directions, whereupon angular momentum might appear to have vanished. Meanwhile in Fermi beta decay transitions the electron and the antineutrino are emitted in similar directions and there’s no change in nucleon spin, whilst in Gamow-Teller transitions the electron and the antineutrino are emitted in opposite directions and there is a change in nucleon spin. The direction of emission matters, because spin is real. The electron is a “dynamical spinor”, which is why electrons and positrons move the way they do in a magnetic field. It’s also a spin ½ particle, as is the proton, as is the neutron. That’s not to say all their spins are all identical, instead they share a spin ½ characteristic. The situation is not unlike odd and even numbers. The numbers three, seven, and eleven are not the same, but they are all odd. If a neutron were to decay into a proton and an electron, it would be like an odd number being broken down into two other odd numbers. We need another odd number to balance the books, another spin ½ particle, the antineutrino. This odd-even type of relationship is why we have even and odd atomic nuclei wherein even-mass-number nuclides are considered to be integer-spin bosons, and odd-mass-number nuclides are considered to be spin ½ fermions.

Radionuclides

Of course back in 1911 Lise Meitner and Otto Hahn were working with radionuclides or radioactive isotopes rather than with free neutrons. One such was bismuth-210. The decay energy for this is 1.16 MeV. The energy spectrum has more or less the same shape as free neutron decay, but the electron and the antineutrino are emitted with more energy. It’s similar for phosphorus-32, where the decay energy is 1.71MeV. This doesn’t sound much compared to the 938MeV mass-energy of the neutron, but it’s a lot compared to the 511keV mass-energy of the electron. The typical beta-particle electron doesn’t just pop out, it’s faster than a speeding bullet. Much faster. It’s so fast it’s relativistic. Using the expression E = m₀c²/√(1-v²/c²) we can work out that a 511keV electron with kinetic energy of 0.2MeV has a speed of just under 0.7c. The beta-particle electron is moving at a significant fraction of the speed of light. The antineutrino is of course moving faster still.

Other beta decays

It’s the same for neutrinos. These were first produced by Frédéric and Irène Joliot-Curie in 1934 when they bombarded aluminium with spin-zero alpha particles to perform beta-plus decay. They called it artificial radioactivity, but we tend to call it positron emission. Given enough added energy, a proton is converted into a neutron plus a positron plus an electron neutrino: p → n + e⁺ + ve. It isn’t really a decay per se, it’s “pushing uphill”: if the neutron was free it would decay into proton with the emission of an electron and an antineutrino. There’s also inverse beta decay. The first example of that was the famous Cowan–Reines neutrino experiment in 1956. Antineutrinos from a nearby reactor combined with protons to produce neutrons and positrons: p + v̄_e → n + e⁺. On top of that there’s electron capture where a proton plus an electron results in a neutron plus a neutrino: p + e⁻→ n + v_e. Then there’s pion beta decay where a negative pion can decay into a neutral pion plus an electron and an antineutrino: π⁻→ π⁰ + e⁻ + v̄_e. Or a positive pion can decay into a neutral pion plus a positron and a neutrino: π⁺→ π⁰ + e⁺ + v_e. There’s a definite Zweig-style tinker-toy aspect to all this. However neutrinoless double-beta decay doesn’t seem to fit the pattern. It is said that this will demonstrate that the neutrino is a Majorana fermion, as opposed to a Dirac fermion. Neutrinoless double-beta decay, which dates back to 1939 and would result in a matter-antimatter imbalance, has not been observed.

Dirac, Majorana and Weyl fermions

What we have observed however, is neutrinos and antineutrinos travelling at the speed of light. Their speed is important when trying to work out what they are. See the Wikipedia fermion article: “mathematically, fermions come in three types – Weyl fermions (massless), Dirac fermions (massive), and Majorana fermions (each its own antiparticle)”. It also says “Dirac fermions can be treated as a combination of two Weyl fermions”. See the Wikipedia spinor article where you can read about Dirac spinors decomposing into a pair of “half-spin” or Weyl representations. Also see Dirac, Majorana and Weyl fermions by Palash Pal. He says “the neutrinos had to be uncharged because of conservation of electric charge, and they seemed to have vanishing mass from the analysis of beta decay data. It was therefore conjectured that the neutrinos are massless. Naturally, it was assumed that the neutrinos are therefore Weyl fermions”. He also said “if neutrinos have mass, they cannot be Weyl fermions”. Whether they do and are, is all to do with helicity and chirality. Make a fist with your left hand and stick your thumb out to your right. A particle moving in the direction of your thumb with a spin in the direction of your fingers has left-handed chirality. Make a fist with your right hand and again stick your thumb out to your right. A particle moving in the direction of your thumb with a spin in the direction of your fingers has right-handed chirality. As demonstrated by the Goldhaber experiment, a neutrino has a left-handed helicity, and an antineutrino has a right-handed helicity:

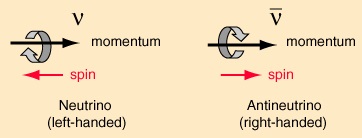Image from of Rod Nave’s hyperphysics

If you could overtake the spinning particle it would appear to move backwards and its helicity will look reversed. Then an antineutrino would look like a neutrino. However you can’t move faster than a particle travelling at c, so you can’t reverse the helicity. This is akin to the absoluteness of electron-positron chirality. The electron has the opposite chirality to the electron, and there is no way you can move to make an electron look like a positron. Apply the same thinking and the nature of the neutrino depends on whether it has mass, which depends on whether it moves at c or not. Do we have evidence of that? I rather think we do.

Neutrinos and antineutrinos travel at c

See Limits on the Neutrino Velocity, Lorentz Invariance, and the Weak Equivalence Principle with TeV Neutrinos from Gamma-Ray Bursts. It’s by Jun-Jie Wei, Xue-Feng Wu, He Gao, and Peter Mészáros, and it dates from 2016. There are some issues with the exact nature of the gamma ray bursts, but they say neutrinos appear to be travelling very close to the speed of light for GRB 11052B, quoting a relative velocity difference of less than or equal to 2.5 x 10^-18. Also see the Wikipedia SN1987A article where you can read this: “approximately two to three hours before the visible light from SN1987A reached Earth, a burst of neutrinos was observed at three separate neutrino observatories”. SN1987A is a supernova that took place circa 168,000 light-years away. Some reports say an initial burst of neutrinos which arrived 7.7 hours before the light. The neutrinos are thought to have been emitted before the light because of the way stars collapse, and in 168,000 years travelling through space, the light didn’t overtake the neutrinos. That suggests neutrinos are massless, which ties in with what Fermi said in section VII of his paper. He plotted three curves and noted that the μ=0 curve matched the empirical curves. He concluded that “the rest mass of the neutrino is either zero, or, in any case, very small in comparison to the mass of the electron”.

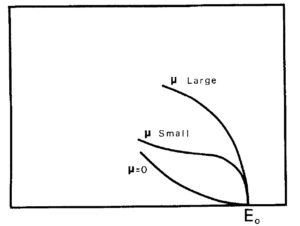Image by Enrico Fermi

Experiments with tritium where the decay energy is a paltry 18keV demonstrate no obvious neutrino mass. See the nuclear and particle physics lecture 21 by Paul Dauncey of the HEP group at Imperial. He says the small energy release makes it easier to observe the effects of a non-zero mass. He goes on to say that neutrino masses of more than 15eV/c² have been excluded, but “it’s very hard to rule out neutrino masses at the level implied by oscillations”. I think it is actually. I think an experiment lasting 168,000 years ruled it out. SN1987A surely trumps a theory that says neutrino oscillation arises “from a mixture between the flavor and mass eigenstates”. Or from a seesaw mechanism based on a mathematical principle that proposes heavy right-handed neutrinos that we’ve never seen. All in all this looks to me like good scientific evidence that the neutrino travels at c just like the photon. And of course in 2011 physicists at OPERA seemingly observed neutrinos travelling faster than light. This was later deemed to be a mistake, but the moot point is that they didn’t see them moving slower than light. Nobody ever has. We have evidence of neutrino oscillation, but we’ve seen enough non-sequiturs already not to jump to conclusions. We’ll come back to neutrino oscillations another day. Meanwhile let’s just say neutrino detection issues do not necessarily mean the neutrino is a Majorana particle with a variable mass. Especially when mass is something we know about. And the wave nature of matter. And electron spin.

What mass is

The mass of a body is a measure of its energy-content. The electron is a body. Electron mass is a measure of resistance to change-in-motion for a wave going around a closed path at c. And because it’s going around that closed path at c, it can’t go linearly at c too. So the electron can never go as fast as light. The photon however is not a body, it’s an E=hc/λ electromagnetic wave. Photon momentum is a measure of resistance to change-in-motion for a wave going linearly at c. It can be a circular-polarized photon with a left hand-helicity or a right-handed helicity. It isn’t the same as the neutrino, but it’s not totally different. Furthermore we have never seen light going slower than light, and we have never seen a neutrino going slower than light either. The hard scientific evidence called SN1987A along with E=mc² says the neutrino is massless, like the photon.

The neutrino is more like the photon than the electron

Not only that, but the hard scientific evidence says the neutrino is more like the photon than the electron. It has no charge like the photon. As far as we can tell it travels at c like the photon, so it has no mass like the photon. The electron has both mass and charge. You can make electrons out of photons in gamma-gamma pair production. You can diffract electrons. In atomic orbitals electrons exist as standing waves. The Poynting vector goes around and around. You don’t need to be Sherlock Holmes to deduce that the electron is a 511keV photon in a closed path, wrapped and trapped in a chiral spin ½ Möbius configuration such that a sinusoidal field-variation looks like an all-round standing field. The neutrino is nothing like that. As for what it is like, in the Wikipedia spinor article we can read about Dirac spinors decomposing into a pair of “half-spin” Weyl representations, presumably like this:

The Dirac-spinor electron

That’s our spin ½ electron, a bispinor where one spin is at twice the rate of the other. Two axial vector currents in sweet harmony. There’s a steering-wheel rotation and a smoke-ring rotation, the former at twice the rate of the other. In one wavelength there are two 360° rotations around the major along with one 360° rotation around the minor axis. If we could somehow remove the major-axis steering-wheel Weyl spinor by making it move downwards, the path of the minor-axis smoke-ring Weyl spinor would no longer be circular. It would be straightened out, so our remaining spinor would exit stage left at the speed of light. We would then have effectively decomposed the electron into two neutrinos moving in orthogonal directions. And as to whether there is a way to do this and ride roughshod over conservation of charge, let’s come back to that another day. For now let’s say the neutrino is like a partial electron, and we made the electron out of a photon in gamma-gamma pair production. So the neutrino is like a photon. Some might even say it’s like half a photon, hence the neutrino theory of light. But a different spin is enough to distinguish the photon and the electron, so I think it’s enough to distinguish the photon and the neutrino too.

The neutrino is rotational wave

The neutrino is like a photon, but not the same. You can emulate a linearly-polarized photon by twanging your washing line. A transverse wave zips down the washing line. You can emulate a circularly-polarized photon by twanging your washing line in two orthogonal directions. A doubly-transverse wave zips down the washing line. To emulate a neutrino you need a pair of pliers. You need to twist that washing line, then let go. A rotational wave zips down the washing line, unwinding the twist. Or if you prefer, the plane-polarized photon is like an arrow with only one pair of flights, whilst the circularly-polarized photon is like an arrow that has one pair of flights set behind the other. It doesn’t rotate, even if the net electric vector does. The neutrino however is like an arrow that has no flights, but which spins like a bullet. In other words the neutrino is a twist in space propagating linearly at c. As it passes you by it’s a momentary magnetic monopole. But it isn’t a real monopole: space isn’t turning continuously. It’s something like the transient rotation that occurs when you turn your wall-mounted hose-reel on. It’s similar to the rotation of the Aharonov-Bohm effect. That’s why the weak interaction violates parity, because it’s the electroweak interaction, and it’s the screw nature of electromagnetism. Hence the Wu experiment is akin to a current loop:

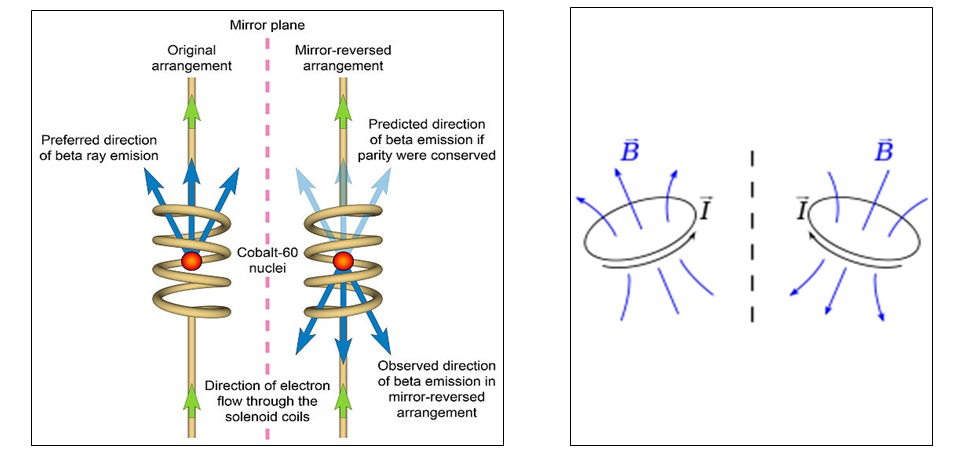        CCASA image by nagualdesign, see Wikipedia                                              Image by Sbyrnes321, see Wikipedia

How much rotation is there in an electron neutrino? There may be a way to work it out, tinker-toy style. Start with the inverse beta decay expression p + v̄_e → n + e⁺. Subtracting p from both sides, we might say that in terms of spin statistics, v̄_e = n – p + e⁺. Substituting p using the beta-plus decay expression p → n + e⁺ + ve gives e⁻ = n – (n + e⁺ + v_e) + v_e which reduces to e⁻ = e⁺ + v_e + v_e. That’s saying that in terms of spin statistics, the electron is equivalent to a positron plus two neutrinos. Let’s say the electron has a right-handed minor-axis rotation whilst the positron with the opposite chirality has a left-handed minor-axis rotation. Then to go from the latter to the former you need to add two left-handed rotations of 360°. This suggests the electron neutrino is a left-handed rotation of 360°, and the electron antineutrino is a right-handed rotation of 360°.

Around and around and around

It also suggests the electron neutrino is a spin ½ particle because it has an odd number of 360° rotations: just one. This in turn suggests the electron is a spin ½ particle that features three 360° rotations: twice round the major axis and once round the minor axis. It would be interesting to throw electrons into an antineutrino flux and look for positrons. Something else that’s interesting is that there seems to be a pattern here. Particles and antiparticles look like they’re just different left-chiral or right-chiral wave-rotation configurations, as suggested by TQFT. So if we know what an electron is, and what a proton is, and what a neutrino is, can we work out what a neutron is? I think the answer is yes. But first I think we need to do some more homework. We need to take a look at electromagnetic gauge theory, the weak interaction, and electroweak theory. And the nuclear disaster.

NEXT