What the proton is not

The proton was discovered by the great Ernie Rutherford in 1917. He used alpha particles to convert nitrogen into oxygen, and in doing so detected hydrogen nuclei. He’d previously done experiments with alpha particles and hydrogen, so he was confident they were hydrogen nuclei. This confirmed William Prout’s hypothesis which dated back to 1815. Prout had observed that the atomic weights of other elements were integer multiples of the atomic weight of hydrogen. So he came up with the idea that the hydrogen atom was a fundamental thing. He called it a protyle, and suggested other atoms were groupings of hydrogen atoms. I think that’s pretty good for 1815. Rutherford more or less confirmed this with the hard scientific evidence, the difference being that the hydrogen nucleus rather than the hydrogen atom was the “fundamental particle”. He called it the proton.

Three quarks for Muster Mark

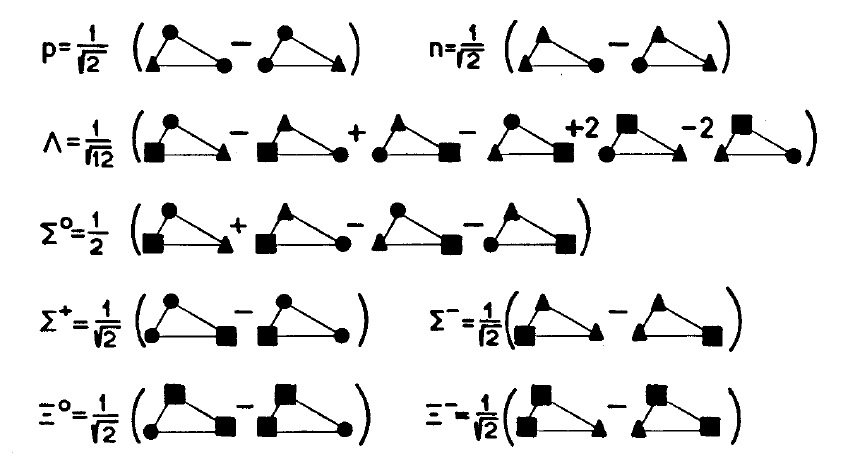
However nowadays you can read that the proton is not a fundamental particle, and instead quarks are. See the particle data group for more about the quark model. This says a meson like a pion is a bound state of a quark and an antiquark, and a baryon like the proton is a three-quark combination. Hence in the Wikipedia proton article you can see this picture:

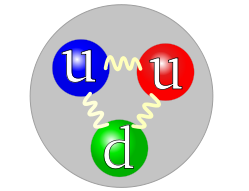CCASA image by Arpad Horvath see Wikipedia

It shows three billiard-ball quarks coloured red green and blue to represent something called color charge. The word color is spelt the American way, without a u, and it isn’t a literal color. The quarks are linked by little springs which represent something called gluons. These are said to mediate the strong force between quarks and so “glue” the quarks together, but note that in ordinary hadrons the gluons are virtual. The u and d characters stand for up and down, which are quark “flavors”. Initially there were three quark flavors, up down and strange, and later charm top and bottom were added. So we have six flavors of quark, and three colors. On top of that there’s antiparticle versions of each quark, each with an anti-color, so there’s six colours in all. There’s also eight types of gluon. The various baryons are said to be comprised of a blue quark, a red quark, and a green quark, or the equivalent anti-quarks. This three-way combination is akin to TV screen colours which together make white, which is no net color. The various mesons are said to be comprised of a quark of a given color and an anti-quark with the corresponding anti-color, again resulting in no net color. The baryons and mesons are said to be “color-neutral”, so you can’t ever see this thing called color. It all sounds reasonable enough, but I’m afraid it’s badly misleading. The picture of the proton above is the wrong picture. It’s a long story. Let’s start from the beginning.

The particle explosion

The electron was discovered in 1897, the proton was discovered in 1917, then the neutron was discovered in 1932, as was the positron. See the Wikipedia timeline of particle discoveries. The muon was discovered in 1937. The charged pion was discovered in 1947, as was the charged kaon. The neutral pion, the neutral kaon, and the lambda baryon were all discovered in 1950. The delta baryon was discovered in 1952. The charged sigma and the charged xi baryon were discovered in 1953. And so on. There’s a useful pictorial list on the particle adventure website:

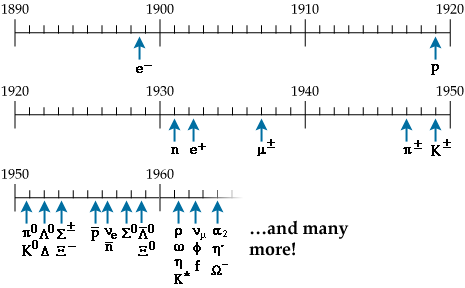Image from the particle adventure

You will find some variation in the dates, for example Rutherford did his experiments in 1917 but reported them in 1919. But regardless of that, it’s clear that from about 1950 there was a whole zoo of supposedly fundamental particles being discovered. It was called the particle explosion, and there was a perception that particle physics was degenerating into something akin to stamp collecting. Wolfgang Pauli said ”had I foreseen that, I would have gone into botany”. Willis Lamb said “the finder of a new elementary particle used to be rewarded by a Nobel Prize, but such a discovery now ought to be punished by a $10,000 fine”. There was a fear that particle physics would be seen as valueless cataloguing, as useful as the study of entrails. Hence particle physicists, both theorists and experimentalists alike, were keen to be seen to be a success. To this end in 1953 Kazuhiko Nishijima developed a formula with Tadao Nakano relating the charge Q of V-particles with isospin I₃, baryon number B, and strangeness S. The formula was Q=I₃+(B+S)/2. In his 1955 paper charge independence theory of V particles, Nishijima referred to various other authors such as Nambu, Yamaguchi, Miyazawa, Oneda, and Pais, and to a property he called eta-charge. Murray Gell-Mann is said to have hit upon the same idea independently a year later in 1956. He referred to the same property but called it strangeness. The formula is nowadays called the Gell-Mann-Nishijima formula. It’s interesting that Gell-Mann’s name comes first.

The V-A interaction

Gell-Mann is an interesting physicist. You can read about him in Ennackal Sudarshan’s glance back at five decades of scientific research. Sudarshan says in 1957 Robert Marshak decided that Sudarshan should present his chiral V-A theory to Gell-Mann over lunch in Santa Monica. Gell-Mann was duly convinced, but told them he didn’t plan to write a paper on it. So Sudarshan wrote up the material, and “rested in peace” from June to September waiting for the big conference in Padua-Venice. However Gell-Mann then wrote a paper with Richard Feynman called the theory of the Fermi interaction. They “asserted” the V-A interaction and merely thanked Marshak and Sudarshan for important discussions. Interesting indeed.

The tenfold way

Meanwhile in 1956 Shoichi Sakata proposed a composite model wherein the various mesons and baryons were composed of four kinds of fundamental particles, namely the ? and the Λ plus their antiparticles, like so:

Image from On a Composite Model for the New Particles by Shoichi Sakata

In 1961 Yuval Ne’eman proposed a classification of hadrons using SU(3) flavour symmetry in a paper called derivation of strong interactions from a gauge invariance. He referred to the Sakata model, and work by Jun John Sakurai and Abdus Salam and John Ward. Gell-Mann is said to have hit upon the same idea independently a year later in 1962. It’s known as the eightfold way, and again there’s some variation in the dates. See the article by George Johnson: “It was rushed into print, and just in time, appearing in February 1962. The Israeli physicist Yuval Ne’eman had independently come up with the same idea. If Ne’eman’s paper hadn’t been bounced because of a formatting problem (his secretary didn’t double-space the manuscript) he would have beat Murray to the punch”. Harry Lipkin gives some useful history of how things progressed in his article from the Sakata model to Goldberg-Ne’eman quarks. We normally think experiments distinguish good model from bad models, but Lipkin says there’s also good and bad experiments, and the latter can have the opposite effect. He also says the discovery of the xi-star particle led Sheldon Glashow and Jun John Sakurai to classify it together with the delta and the sigma particles in the tenfold way and predict the existence of an isoscalar baryon with strangeness -3. He says “to an unbiased observer, the credit for the prediction of the existence of the Z⁻, now called the Ω⁻, belongs to Glashow and Sakurai”. They predicted it in a paper called 27-fold way and other ways: symmetries of mesons-baryon resonances. It was received by Nuovo Cimento in April 1962. However Gell-Mann got the credit for it. Lipkin goes on to say Hayim Goldberg and Yuval Ne’eman’s 1963 paper on baryon charge and R-inversion in the octet model anticipated the quark model. Gell-Mann get the credit for that too. All interesting stuff.

The eightfold way

For some more interesting stuff see the reader-friendly historical article on the eightfold way by Jonathan Rosner. He tells us about the strange feature of certain particles which decay relatively slowly. “Slowly” is debateable, since the charged kaon decays in circa 1.238 × 10⁻⁸ seconds. But no matter, such particles were assumed to have the property of strangeness which is preserved in production but not necessarily in decays. This strangeness is plotted against charge to yield the baryon and meson octets:

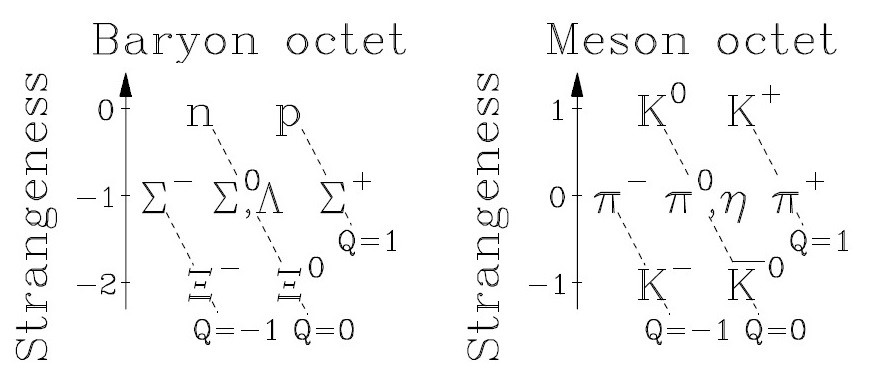Image by Jonathan Rosner

There’s a slightly different version of Rosner’s article on the arXiv. You can read that “Both the mesons and the baryons mentioned above would then have to belong to eight-member families. The baryons fit such a family exactly, leading Gell-Mann to call his scheme the Eightfold Way”.

Predicting the omega minus

You can also read that certain baryons known as Δ (delta), Σ* (sigma-star), and Ξ* (xi-star) appeared to fit into a ten-member triangular family, which would be completed by a not-yet observed particle known as the Ω⁻ (omega-minus). Rosner goes on to say the mass of the Ω⁻ could be anticipated to a few percent because the Gell-Mann-Okubo mass formula predicted the same mass difference between each particle. It’s about 147MeV. See the UPenn citation classic dated September 8^th 1980 for more. Susumu Okubo said it took him two months hard work at CERN in 1960-61 to come up with the mass formula. He also said a special case of the mass formula was discovered by Gell-Mann a year later in his 1962 paper on the symmetries of baryons and mesons, so the formula is now known as the Gell-Mann-Okubo mass formula. Presumably Gell-Mann hit upon the same idea independently. Also see the omega minus blog article by Sabine Hossenfelder. She refers to various sources and says Ne’eman had submitted an abstract to the June 1962 CERN conference but wasn’t given a slot to talk about it. She also says “Ne’eman was confident that there should be an isosinglet resonance with S=-3, negative electric charge, spin 3/2, and a mass of about 1680 MeV, and he decided to make this point in the discussion following a review talk on the new baryonic resonances”. He raised his hand to speak, but so did Gell-Mann, who had hit upon the same idea independently. Gell-Mann got picked because he was more eminent. Or perhaps as Frank Close said in quantum theory, because he was nearer the front. Either way, it was Gell-Mann who predicted the properties of the missing particle, and named it. It was Gell-Mann who got the credit for it.

Detecting the omega minus

Also see the 20^th February 1964 New Scientist article order out of sub-nuclear chaos. In it Paul Matthews talked about the anticipated discovery of the Ω⁻ particle at Brookhaven where they had an alternating-gradient synchrotron and an eighty‐inch bubble chamber. He gave a potted history, referring to Ohnuki’s new spins and saying the masses of the various particles are analogous to the energy levels of atomic or nuclear systems. I’m not sure when he filed his copy but Robert Crease reports that the Ω⁻ was discovered on February 9^th 1964. The paper observation of a hyperon with strangeness minus three by Virgil E Barnes et al was published in Physical Review Letters on February 24^th. See the Brookhaven article on the discovery of the Ω⁻ particle. It describes how in the early sixties theorists “found in group theory a ready-made mathematical description that seemed to provide a remarkably successful scheme for classifying the then known hadrons”. It goes on to say that it was hoped that this scheme might lead to an understanding of particle structure, and that it was very important that the validity of SU3 be demonstrated by experiment. Hence it was a “major triumph” when the Ω⁻ was discovered by a team led by Nicholas Samios. Other reports such as physics today say the experiment was performed by a team of thirty‐three physicists headed by Ralph Shutt with Nick Samios in direct charge of the experiment. Here’s the bubble-chamber photograph with a cleaned-up drawing next to it:

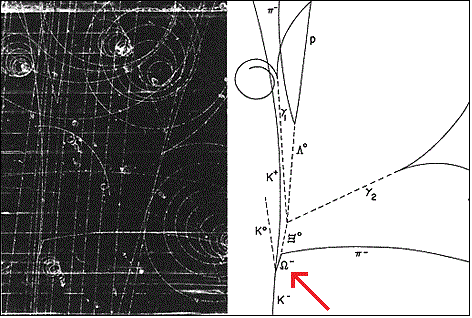Bubble chamber photograph and drawing from the Brookhaven National Laboratory

I’ve pointed out the Ω⁻ track with a red arrow. At 2cm long it’s rather short. Even though the Ω⁻ is said to be comprised of three strange quarks and strangeness is associated with longevity, the particle doesn’t last long. It’s somewhat ephemeral, and the photograph reminds me of night-time fireworks. In 10^-10 seconds the Ω⁻ has decayed into a negative pion and a neutral xi, which doesn’t leave a track. The dotted line has been filled in by hand. The neutral xi then decays in less than a nanosecond into a neutral lambda and a two gamma photons, none of which leave any tracks. Three more dotted lines have been filled in by hand. Moreover on hyperphysics Rod Nave reminds us that “actually, the primary decay of the xi is to a lambda-zero and a pi-zero. It is just that the π⁰ decays into two gammas with a lifetime of about 10^-16 seconds, so the two gamma rays appear to come from the same point as the lambda“. The neutral pion has no track, the length of its track is effectively zero. All in all it isn’t particularly impressive to a member of the public. Particularly since the spin of the Ω⁻ wasn’t measured. It still wasn’t measured even forty years later. See the 2008 paper measurement of the spin of the Ω¯ hyperon at BABAR. The Ω⁻ was widely publicised and billed in the New Yorker and The Sciences and elsewhere as “the kingpin” particle, but on closer examination there’s less to it than meets the eye. Nowadays we might say it was hyped, which is rather ironic, because the Ω⁻ is a hyperon. Also see the Wikipedia omega baryon article which says the discovery was a great triumph in the study of quark processes. But note that there’s no mention of quarks in the 1964 Brookhaven paper. Quarks weren’t flavor of the month yet, not by a long chalk.

The quark model

George Zweig’s memories of Murray and the quark model makes for interesting reading. He says Gell-Mann’s modus operandi was to come up with a toy model that he was prepared to jettison, like cooking pheasant between two slices of veal. He also talks about the spring of 1963. That’s when Bob Serber talked about a scheme wherein baryons were made from “three fundamental representations of SU(3) (3 x 3 x 3)” and mesons were made from a fundamental representation and an antiparticle of the same. Zweig goes on to say this: “After a moment’s calculation Murray [Gell-Mann] found that this would imply that the members of the fundamental representation would have fractional charge, a fact that Serber had not realized. No more was said, but in February of 1964 Murray proposed using the three fractionally charged objects in the fundamental representation as fields from which to construct the currents of a toy field theory”. Interesting. It’s also interesting that Zweig was one of Gell-Mann’s students. See his origins of the quark model. In the spring of 1963 he was working on his thesis which was all about particles being composite objects comprised of “aces”, rather like tinker-toy parts that snap together. By January 1964 Zweig had proposed that “both mesons and baryons are constructed from a set of three fundamental particles called aces”.

Aces image from George Zweig’s origins of the quark model

Gell-Mann hit upon the same idea independently, but used the name quarks. Again there’s some variation in the dates, but again, it’s all interesting stuff. See the CERN fifty years of the quark article. Also see the big and the small by Ganeshan Venkatamaran where you can read that Zweig was at CERN and had to send his paper to Physics Letters, but had problems with the editor and the referees. Also see Zweig’s CERN interview where he said Leon Van Hove “deliberately and systematically tried to keep my work from public view”. Hence Zweig’s paper remained as an unpublished CERN document whilst Gell-Mann published his own paper and established priority. Gell-Mann’s paper was a schematic model of baryons and mesons, and was a mere two pages long.

A mathematical figment

In it Gell-Mann said “it is fun to speculate about the way quarks would behave if they were physical particles of finite mass (instead of purely mathematical entities as they would be in the limit of infinite mass)”. He was suggesting that they were abstract mathematical things, like elements of a pattern. But his paper, apart from thanking Bob Serber for stimulating his ideas, ends thus: “A search for stable quarks of charge -1/3 or +2/3 and or stable di-quarks of charge -2/3 or +1/3 or +4/3 at the highest energy accelerators would help to reassure us of the non-existence of real quarks”. Gell-Mann was hedging his bets. George Johnson says one colleague described Gell-Mann’s position thus: “If quarks are not found, remember I never said they would be; if they are found, remember I thought of them first”. Thus the quark model was born, fireproofed from day one.

Like a lead balloon

Initially however the quark model went down like a lead balloon. For starters it wasn’t popular because of the fractional charge. Here was a theory saying the various observed particles are made up of particles with fractional charge, but nobody had ever seen a particle with fractional charge. Nobody had ever seen a quark either, even though they’d seen a whole zoo of other particles that were supposed to be comprised of quarks. Moreover quarks were supposed to be spin ½ particles, and there were supposed to be three of them in the Ω⁻ particle, with their spins aligned. See Harald Fritzsch’s history of QCD. He says the Ω^– is in breach of the Pauli exclusion principle and that this was “a great problem for the quark model”. It’s the same issue with the delta plus-plus Δ⁺⁺ comprised of three up quarks, and the delta minus Δ⁻ comprised of three down quarks. On top of that the masses didn’t square. The 938 MeV proton was said to be made up of three quarks and nothing else, suggesting a quark mass of circa 310 MeV. That worked for the 940 MeV neutron too. But the 140 MeV charged pion was said to be made up of a quark and an antiquark, suggesting a quark mass of 70 MeV. Something didn’t add up. Something was wrong with the quark picture.

Color and gluons and charm and epicycles

In the same year that the eightfold way had been acclaimed via the discovery of the Ω⁻, the quark model had fallen at the first hurdle. But when a church needs a miracle, a church gets a miracle. So as Andrew Watson says in the quantum quark, Oscar Greenberg came up with a “fix” for the Pauli Exclusion problem. Moo-Yung Han and Yoichiro Nambu came up with a fix too. It was a further 3-value attribute on top of up down and strange, which would eventually become color charge. It came with excess baggage in the form of gluons and eight gluon fields. See the CERN courier article twenty-five years of gluons. It says “the only stable states formed by them are colourless combinations, a hypothesis that sounded at first like sleight of hand”. On top of that Sheldon Glashow was now advocating a 4-value proposal with an extra quark. It was all too soon. In George Johnson’s strange beauty you can read that “for doubters these elaborations were reminiscent of Ptolemy”. Ptolemy was the man who invented epicycles. See Kazuo Fujikawa’s in memory of Akira Tonumura: “fractional charge was an unpopular idea, and most physicists thought that this was one of the reasons why the quark model could not be correct… physicists searched for quarks in every possible way, looking at accelerator production, cosmic rays, the terrestrial environment, sea water, meteorites, air, etc. No quarks were found in any of these searches… the general point of view in 1966 was that quarks were most likely just mathematical representations: useful but not real”. So Gell-Mann might have been feeling rather unhappy, despite hedging his bets.

An infinite number of pointlike partons

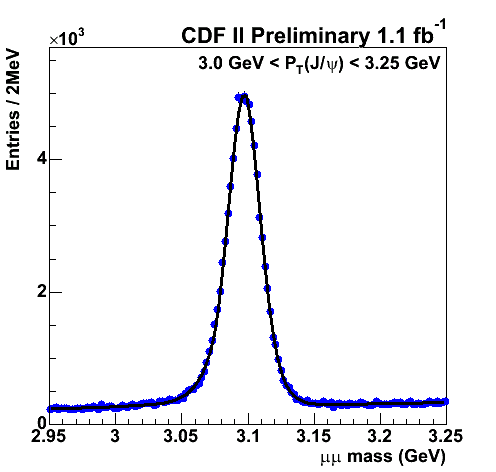
George Johnson also wrote the jaguar and the fox, which tells of the rivalry between Gell-Mann and his Caltech colleague Richard Feynman. Feynman was coming up with a theory of partons in direct competition to the quark model. Gell-Mann sneeringly referred to partons as “put-ons”. I fancy that David Goodstein nailed it with “Murray Gell-Mann was the smartest person on Earth, except maybe for the guy in the next office”. Gell-Mann must surely have been unhappy about what was coming out of SLAC. See Finn Ravndal’s how I got to work with Feynman on the covariant quark model. He tells how in 1968 he went to Caltech taking a Russian paper by P N Bogoliubov about the proton being made up of three quarks. He goes on to say “at one of the first institute colloquia the invited speaker was J Bjorken from SLAC who talked about deep inelastic scattering and the parton model. The proton contained an infinite number of these new particles”. An infinite number of partons? That sounds as if this must have been pretty grim for Gell-Mann, particularly since “the atmosphere was electric” and “Feynman in the front row was smiling”. Particularly since Ravndal also says “the old quark model seemed no longer to be relevant in this context”. But he also says “Gell-Mann beside him was visibly excited”. You can see why when you take a look at inelastic electron-proton and gamma-proton scattering, and the structure of the nucleon by James Bjorken and Emanuel Paschos. They talk about partons, keeping Feynman happy, but they also talk about quarks, keeping Gell-Mann happy. They have their cake and eat it by talking about three valance quarks in a pion-cloud “sea” of quark-antiquark pairs. However quarks were still not accepted. When Gell-Mann was awarded the 1969 physics Nobel prize it wasn’t for quarks. It was for “his contributions and discoveries concerning the classification of elementary particles and their interactions”. In his 2001 book great physicists, William Cropper says quark theory was still tenuous enough that the Nobel citation said nothing about it. It wasn’t until 1974 and the November revolution that quarks caught on, because of the “discovery” of the J/Psi meson at SLAC and Brookhaven. It had a lifetime of 7.2×10^-21 seconds, so its existence was inferred from a narrow resonance in electron-positron annihilation:

Public domain Fermilab image, see Wikipedia commons

There was no particle track. Just a bump on a graph, one that “proved” that quarks were real. In similar vein the gluon was “discovered” in the 1979 TASSO experiment using the PETRA accelerator at DESY. Gluons weren’t seen in a detector, their existence was inferred. See Y(9.46 GeV) and the gluon discovery by Bruno Stella and Hans-Jürgen Meyer. They slammed electrons and positrons together, and when they saw three jets, it “proved” that gluons were real.

Zillions of quarks and gluons

And so it came to pass that partons and quarks became one, thence the existence of quarks and gluons was proven, and they all lived happily ever after. But fast forward to the present day and check out what professor and blogger Matt Strassler has to say. He’s a member of the CMS collaboration at CERN. See his article what’s a proton anyway? He says this: “You may have heard that a proton is made from three quarks. Indeed here are several pages that say so. This is a lie – a white lie, but a big one. In fact there are zillions of gluons, antiquarks, and quarks in a proton”.That’s a surprise to most people. Most people think the proton is made up of two up quarks and a down quark, plus gluons. But that’s not what Strassler says. He says the usual picture of a proton as being composed of three quarks joined by elastic-spring gluons is misleading. He says it’s impossible to describe the proton’s structure simply. He says all the zillions of quarks and antiquarks and gluons inside are rushing around inside at nearly the speed of light. Here’s his depiction:

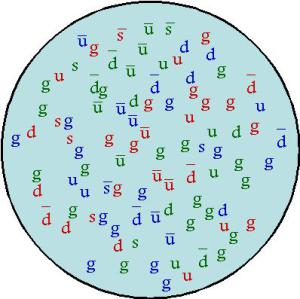Image by Matt Strassler

He says the proton isn’t really made of two up quarks and one down quark. Instead he says it has two more up quarks than up antiquarks, and one more down quark than down antiquarks. You might think Matt is talking out of his hat here, because he’s totally contradicting the quark model developed in the sixties. Particularly if you know that the gluons in ordinary hadrons are virtual, that sea quarks are virtual too, and that virtual particles only exist in the mathematics of the model. But Matt isn’t making it up. He’s telling you about quantum chromodynamics. The trouble is that when you piece the puzzle together, you appreciate that even this new picture is the wrong picture. You appreciate that the proton is not some host of quarks and gluons ready to come spilling out like beans from a bag. You appreciate what the proton is not. The proton is not three quarks glued together by three gluons, and nor is it zillions of quarks and gluons. So what is it?

NEXT