The TOE that Maxwell missed

If you’ve ever read James Clerk Maxwell’s 1865 paper A Dynamical Theory of the Electromagnetic Field, you might have noticed his Note on the Attraction of Gravitation. It’s at the end of part IV. Maxwell ends up saying energy is essentially positive, and that “the presence of dense bodies influences the medium so as to diminish this energy wherever there is a resultant attraction”. Then he said this: “As I am unable to understand in what way a medium can possess such properties, I cannot go any further in this direction in searching for the cause of gravitation”. This is a great shame. He thought there was a back-to-front energy density, and then he gave up.

Things are often back to front in physics

It’s an easy mistake to make. Things are often back to front in physics. For example in electromagnetism, electricity is back to front. You’d think that electricity flows through a wire from the positive terminal of a battery to the negative terminal, but it doesn’t. It goes the other way:

Image from XKCD

Things are sometimes back to front in gravity too. See for example Opticks query 20: “Doth not this aethereal medium in passing out of water, glass, crystal, and other compact and dense bodies in empty spaces, grow denser and denser by degrees, and by that means refract the rays of light not in a point, but by bending them gradually in curve lines?” Newton got his density gradient back to front. In similar vein people say gravitational potential energy is negative when it isn’t. The expression U = -GMm/r is badly misleading. Anyway, Kevin Brown says something about Maxwell and gravity in his mathspages article Why Maxwell Couldn’t Explain Gravity. He says the gravity between two bodies is akin to the electrostatic force between two particles with the same charge, so it ought to be repulsive. He also says “the only possibility that Maxwell could see for salvaging the field-based approach to gravity was if we suppose that a massive body contributes negatively to the energy of the gravitational field in its vicinity”. On top of that Brown says “the modern textbook explanation today is that the total mass-energy of a system is indeed reduced when the matter components are in closer proximity, just as Maxwell surmised”. That isn’t the whole truth, because conservation of energy applies. Maxwell knew about the conservation of energy. He talked about it in part IV of his paper, just after equation (40). He also knew about kinetic energy and potential energy. Google it. So I definitely think he gave up too soon. If he’d stuck to conservation of energy he would have surely known that something was back to front. Then the scales would have fallen from his eyes.

If only he’d turned figure 6 on its side

But they didn’t. Check out what he was still saying eight years later. See the preliminary section of his 1873 Treatise on Electricity and Magnetism. He said this: “In the theory of gravitation the potential is taken with the opposite sign to that which is here used, and the resultant force in any direction is then measured by the rate of increase of the potential function in that direction”. He didn’t challenge this potential with an opposite sign. Even though by then he must have known he’d got his vortices back to front because he’d reverted to Ampère’s molecular vortices. The vortex was now in the matter, not in space. If only Maxwell had thought of that, then revisited his 1861 paper On Physical Lines of Force. If only he’d turned figure 6 on its side:

Excerpt from James Clerk Maxwell’s On Physical Lines of Force

I really mean all this. In part IV/chapter XI of his treatise Maxwell said we must give up the old theory of magnetism, and adopt that of Ampère, “which admits of no magnets except those which consist of electric currents”. He also said we must also regard both magnetic and electromagnetic energy as kinetic energy. Then in the preliminary section of his treatise he missed his own clue when he said the unit of mass is “made to depend on the value of the force of gravity”. It’s as if there’s something missing. Search his treatise for instances of Newton. He refers to Ampère as the Newton of electricity. He talks about the popularization of correct dynamical ideas since the time of Galileo and Newton. He talks about Newton’s notation. He talks about Newton’s Principia. But there’s no mention of Newton’s aethereal medium.

The punchline comes at equation (132)

I find it surprising, because of the very genesis of Maxwell’s electromagnetism. Maxwell was into aether in a big way. In his 1861 paper On Physical Lines of Force, he said the stress along the lines of gravitating force must be a pressure. He was right about that. But he even though he knew that the force of gravity decreased in line with the inverse square rule, and even though he was treating space as an elastic medium, he didn’t pursue it. Take a look at the Wikipedia talk page for On physical lines of force. It dates back to 2010. Contributor David Tombe says “the punchline comes at equation (132) where he uses the Weber/Kohlrausch experimental result in Newton’s equation for the speed of sound”:

Excerpt from James Clerk Maxwell’s On Physical Lines of Force

Maxwell used Newton’s equation. The one that said the speed of a transverse wave in an elastic medium was V =√(m/ρ), where “m is the coefficient of transverse elasticity, and ρ is the density”. He referred to a coefficient of magnetic induction, but it’s the same difference. If the density increases, the speed decreases. Maxwell knew about Huygens, who along with others “developed the undulatory theory”. So he must surely have known that light is refracted when the medium changes. And that the pressure changes in line with the inverse square rule? Surely?

They came up with the speed of light in 1855 using a Leyden jar

Nowadays we write Maxwell’s expression down as c = 1/√(ε₀μ₀). That says the speed of light depends on the permittivity and permeability of space. Amazingly this dates back to 1855, when Maxwell was still talking about sources and sinks. Take a look at the Wikipedia article on the history of Maxwell’s equations. I don’t know who wrote it, but it’s good stuff. Thanks guys:

The discovery of this relationship started in 1855, when Wilhelm Eduard Weber and Rudolf Kohlrausch determined that there was a quantity related to electricity and magnetism, “the ratio of the absolute electromagnetic unit of charge to the absolute electrostatic unit of charge” (in modern language, the value 1/√(ε₀μ₀)), and determined that it should have units of velocity. They then measured this ratio by an experiment which involved charging and discharging a Leyden jar and measuring the magnetic force from the discharge current, and found a value 3.107×10⁸ m/s, remarkably close to the speed of light, which had recently been measured at 3.14×10⁸ m/s by Hippolyte Fizeau in 1848 and at 2.98×10⁸ m/s by Léon Foucault in 1850. However, Weber and Kohlrausch did not make the connection to the speed of light. Towards the end of 1861 while working on part III of his paper On Physical Lines of Force, Maxwell travelled from Scotland to London and looked up Weber and Kohlrausch’s results. He converted them into a format which was compatible with his own writings, and in doing so he established the connection to the speed of light and concluded that light is a form of electromagnetic radiation.

I think that’s amazing. Wilhelm Weber and Rudolf Kohlrausch came up with the speed of light in 1855 using a Leyden jar. A battery. But they didn’t know it was the speed of light until Maxwell nailed it in 1861. Or so it would seem. Like David Tombe I’m not sure of that because in 1857 Gustav Kirchhoff “calculated that an electric signal in a resistanceless wire travels along the wire at the speed of light”. It would seem that Kirchhoff made the connection between electricity and the speed of light years before Maxwell, but didn’t realise that light was an electromagnetic wave in space.

It’s like light is an alternating current in a lossless transmission line of its own making

Kirchhoff’s paper was on the motion of electricity in wires. I didn’t get it myself, it isn’t the clearest paper I’ve ever tried to read. But I did a Computer Science degree. I know that the speed of a signal down a transmission line like a coaxial cable depends on its inductance and capacitance. The expression is v = 1/√(LC):

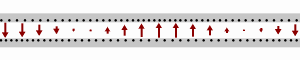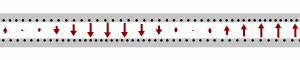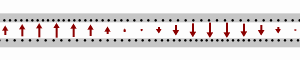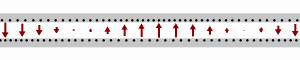
Transmission line Gif by Sbyrnes321, see Wikipedia.
Caption: “A wave traveling rightward along a lossless transmission line. Black dots represent electrons, and arrows show the electric field”.

I also know that the impedance of the line is Z₀ = √(L/C), and that impedance is resistance to alternating current. I also know that the impedance of free space is Z₀ = √(μ₀/ε₀), and is 376.73 Ohms. So I know that the speed of light in space depends on the permeability and permittivity of space. The expression is c = 1/√(ε₀μ₀). It’s like light is an alternating current in a lossless transmission line of its own making. An alternating displacement current going this way ↑ then that way ↓ whilst propagating through space this way →. I know that if you change the impedance or the capacitance you change the signal speed. Kirchhoff knew it too. But I’m not sure Maxwell did.

The velocity of light in different media is inversely proportional to their indices of refraction

Maxwell repeated the speed of light stuff in his 1865 Dynamical Theory of the Electromagnetic Field. See part VI. He said Weber and Kohlrausch’s results showed that “ν = 310,740,000 metres per second is the number of electrostatic units in one electromagnetic unit of electricity, and this, according to our result, should be equal to the velocity of light in air or vacuum”. Then Maxwell gave a variety of measured and deduced speeds of 314,858,000, 298,000,000, and 308,000,000 m/s. Now take a look at chapter XX of his 1873 treatise. He said “the velocity of light in different media is inversely proportional to their indices of refraction”. He also knew that light was intimately connected to Ampère’s molecular vortices. He knew that Faraday thought of particles as parts of space where forces converged. He must have known about Opticks query 30 where Newton said “are not gross bodies and light convertible into one another?” Surely? I have to wonder if he ever actually read that. Or Newton’s query 20. Here it is again: “Doth not this aethereal medium in passing out of water, glass, crystal, and other compact and dense bodies in empty spaces, grow denser and denser by degrees, and by that means refract the rays of light not in a point, but by bending them gradually in curve lines?” Maxwell knew that c = 1/√(ε₀μ₀) , but it looks like he didn’t think of permittivity and permeability varying in a gravitational field.

Newton’s aether model

A little bit of detective work on the internet turns up Eric Baird’s 2000 paper Newton’s aether model. He says modern textbooks typically say that Newton believed that space and time were absolute and inviolable. Then he says this: “However, a reading of Newton’s ‘Principia’ and ‘Opticks’ reveals a rather different picture, with Opticks in particular documenting Newton’s attempt to produce a model of gravity in which a gravitational field could be represented as a series of light-distance differentials, or as a variation in lightspeed or refractive index”. Good stuff Eric. Why have I never heard of you before? And what else have you got to tell me? Uh huh: “This can be compared to Einstein’s ‘refractive’ approach to gravitational light-bending in 1911 and to his description of general relativity as a (nonparticulate!) gravitational aether model in 1920”. Excellent. Baird then gives Newton’s back-to-front view, that “the falling of light-corpuscles in a gravitational field can be described as the deflection of light towards regions of higher lightspeed”. Then he gives Huygen’s view: “If a light-signal wavefront encounters a lightspeed gradient across its surface, with a faster natural speed on one side and a slower speed on the other, the retardation of the wavefront’s slower side will steer the wavefront towards the slower-speed region”. As we know, Huygen’s view is correct:

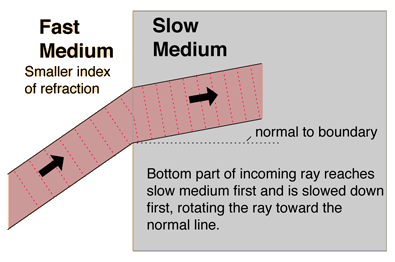Refraction image from Rod Nave’s hyperphysics

Baird then says we can make Newton’s description compatible with Huygens’ principle by inverting his lightspeed and aether-density relationships. This is great, it’s like finding AS carved on the wall of the cavern. This guy was playing physics detective twenty years before me. Then he says this: “the disagreement between Newton’s and Huygens’ arguments and the subsequent disproof of Newton’s lightspeed predictions (Foucault, 1850) had serious consequences for the idea of wave-particle duality, with Opticks going out of print until 1931, and its contents apparently unknown to Einstein as late as 1921”. What? Maxwell didn’t know about Newton’s Opticks? FFS. Baird also says Maxwell thought of William Kingdon Clifford’s work as “the work of a space-crumpler”. Jeez. You learn something new every day.

We would have had an initial theory of everything in 1870

Maxwell combined the electric field and the magnetic field to give us the “greater whole” called the electromagnetic field. Then he threw in light, in what was a precursor to QED, the “strange theory of light and matter”. But it looks like Maxwell didn’t know about Newton’s aethereal medium growing denser and denser by degrees. It looks like Maxwell didn’t know that the speed of light is not constant in vacuo. If he had, he could surely have applied his certain knowledge that energy is positive and is always conserved. Then he would have soon worked out that the kinetic energy of a falling body comes from that falling body, and not from the field. Then he would have worked out that the potential energy was positive, and was in that falling body, because it was mass-energy. He would have worked out that gravity was merely a refraction, a trick of the light that converted internal kinetic energy into external kinetic energy. Then when this external kinetic energy is dissipated you’re left with a mass deficit. Just like in electromagnetism:

Image from Rod Nave’s hyperphysics

That’s why U = -GMm/r is badly misleading. Because when you lift a brick, you do work on it. You add energy to it. So you increase its mass. So m changes. Knowing this, Maxwell would have flipped his showstopper issue. He would have known that “the presence of dense bodies influences the medium so as to increase its energy wherever there is a resultant attraction”. He would have known that a gravitational field was a pressure-gradient in space. Or an energy-density gradient if you prefer. He would have known how gravity works. He would probably have known about E=mc² and about mass. Then we would have had an initial theory of everything. In 1870. A TOE that combined electricity, magnetism, light, and gravity. Shortly followed by the worble embracing itself. Ampère’s molecular vortex. The electron. The “dynamical spinor”. Understand all that, and the rest is just mopping up.

NEXT