In the Wikipedia dark energy article you can read how the term “dark energy” was coined by Michael Turner in 1998. This was in a paper co-authored with Dragan Huterer called prospects for probing the dark energy via supernova distance measurements. It referred to the type 1a supernovae observations made by the Supernova Cosmology Project and by the High-Z Supernova Search Team. Their observations indicated that the expansion of the universe is accelerating, which was contrary to expectations and led to Nobel prizes in 2011:
Expanding universe image from the NASA Goddard Space Flight Centre
However dark energy goes arguably back further than that. As to how far, it’s hard to say. There’s an interesting historical paper by Helge Kragh dating from 2011 called Preludes to dark energy: Zero-point energy and vacuum speculations. He starts by saying “according to modern physics and cosmology, the universe expands at an increasing rate as the result of a “dark energy” that characterizes empty space”. Kragh also talks about Walther Nernst’s zero-point energy hypothesis dating from 1916. He says “to many physicists and cosmologists, the cosmological constant and the zero-point energy density of vacuum are just two names for the same thing”. That’s interesting.
Vesto Slipher measures galactic redshift
Another interesting historical paper was written by Cormac O’Raifeartaigh in 2012. It’s on the contribution of VM Slipher to the discovery of the expanding universe. Way back in 1913 Vesto Slipher had measured a blue-shift for the Andromeda nebula equivalent to 300 km/s. By 1917 he had results for 25 spiral nebulae, of which 21 were red-shifted, by up to 1100 km/s. O’Raifeartaigh says “such large recession velocities were a great anomaly and suggested to some that the spirals could not be gravitationally bound by the Milky Way. Thus, Slipher’s redshift observations became well-known as one argument for the ‘island-universe’ hypothesis”. But not known to Einstein, it would seem.
Einstein’s cosmological constant §1
Dark energy is often considered to have originated with Einstein’s cosmological constant. See O’Raifeartaigh’s 2017 Physics Today article Albert Einstein and the origins of modern cosmology. It’s about Einstein’s general relativity wherein Gμν = -κTμν. The Gμν term is a tensor that describes the geometry of a region of spacetime, Tμν is a tensor that describes the stress-energy-momentum within that region, and κ is the Einstein constant. The article is also about Einstein’s 1917 paper which added a λgμν term and “laid the foundations of modern theories of the universe”. As such, Einstein’s 1917 paper deserves careful attention. It was called cosmological considerations in the general theory of relativity. In the introduction Einstein talked about Poisson’s equation ∇²φ = 4πκρ and how he might describe “boundary conditions” for gravitational potential in an infinite universe. In section §1 Einstein talked about the “Newtonian system of the universe”. He was referring to a universe consisting of an island of stars in an infinite ocean of space. Einstein likened stars to gas molecules and said if we apply Boltzmann’s law the Newtonian stellar system can’t exist because “a vanishing of the density at infinity thus implies a vanishing of the density at the centre”. He then proposed ∇²φ – λφ = 4πκρ with an extra lambda term, and described a scenario where on the largest scale matter was distributed uniformly, resulting in a uniform potential on that largest scale. He said such a universe would have no centre with respect to its gravitational field, and that matter would be in equilibrium “without any internal material forces (pressures) being required”. This sounds reasonable. It’s akin to Newton’s infinite universe, which avoids collapse because all stars are surrounded by other stars. But see Newton and the infinite universe written by Edward Harrison in 1986. Note that “rotating sidereal systems, considered by the imaginative Thomas Wright in 1750, received no attention from Bentley and Newton”. Or from Einstein, it would seem.
Einstein’s cosmological constant §2
In section §2 Einstein said “in a consistent theory of relativity there can be no inertia relatively to ‘space’, but only an inertia of masses relatively to one another”. This is Mach’s principle, and it doesn’t sound reasonable at all. Particularly when Einstein said this: “If, therefore, I have a mass at a sufficient distance from all other masses in the universe, its inertia must fall to zero”. This contradicts E=mc² wherein “the mass of a body is a measure of its energy-content”. Particularly since on the next page Einstein said potential energy “becomes infinitely great at infinity”. The trouble with that is as per Gustav Mie’s 1915 mass deficit description, potential energy is mass energy, so if the potential energy increases, inertia should increase too. Fortunately with the assistance of Jacob Grommer, Einstein abandoned this approach. He said two possibilities next present themselves: a) gμν at spatial infinity approximates to a given tensor value, and b) gμν is only given for the spatial limit of the domain under consideration. He rejected the latter as giving up. But he also rejected the former because it pre-supposes “a definite choice of the system of reference, which is contrary to the spirit of the relativity principle”. Of course he didn’t know about the CMBR dipole anisotropy back then:
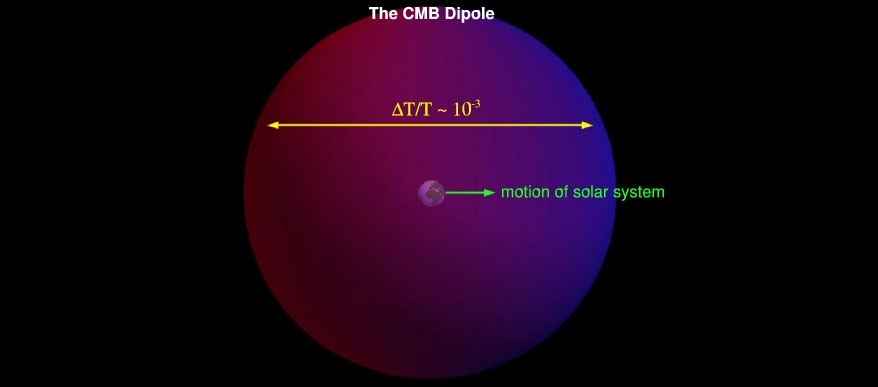CMB dipole image by William Kinney and NED
Einstein also rejected the former option because it failed “to comply with the requirement of the relativity of inertia”. But he said there was a possible way out: “if it were possible to regard the universe as a continuum which is finite (closed) with respect to its spatial dimensions, we should have no need at all of any such boundary conditions”. In subsequent sections Einstein described a curved closed hypersphere universe: if you keep going thataway, you end up coming back thisaway, like the old asteroids game. Note though that Einstein’s cosmological constant didn’t cause the curvature. Einstein finished thus: “It is to be emphasized, however, that a positive curvature of space is given by the presence of matter27, even if the supplementary term is not introduced. That term is necessary only for the purpose of making possible a quasi-static distribution of matter, as required by the fact of the small velocities of the stars”.
Puzzling aspects
O’Raifeartaigh says a puzzling aspect of Einstein’s paper is that Einstein made no attempt to estimate the size of his model universe, or consider its stability. He makes that point that a slight increase in density would trigger a contraction, and “a slight decrease would result in a runaway expansion”. For me a more puzzling aspect of the paper is why Einstein was talking about an “outlandish“ curvature of space when a gravitational field is a place where space is neither homogeneous nor isotropic. Or why he thought of space as some kind of empty arena for matter. Or why he didn’t think of a universe where matter was rotating, as per the solar system. After all, back in 1917 most people thought the island universe was the Milky Way. See Wikipedia: “in a treatise in 1755, Immanuel Kant, drawing on earlier work by Thomas Wright, speculated (correctly) that the Milky Way might be a rotating body of a huge number of stars, held together by gravitational forces akin to the Solar System but on much larger scales”. Kant also suspected the nebulae were galaxies in their own right. All in all I definitely think my hero Einstein was in greatest blunder territory here.
The de Sitter universe
It seems that a hundred and two years earlier, Willem de Sitter felt the same. He was Einstein’s contemporary and correspondent. He signed his letters ihr ganz ergebener: your most devoted. See his 1917 paper On the relativity of inertia. Remarks concerning Einstein’s latest hypothesis. He was not enamored of Mach’s principle: “If all matter is supposed not to exist, with the exception of one material point which is to be used as a test-body, has then this test-body inertia or not? The school of MACH requires the answer No. Our experience however very decidedly gives the answer Yes”. He didn’t seem fond of Einstein’s closed universe either: “If the gμν at infinity are zero of a sufficiently high order, then the universe is finite in natural measure”. Interestingly, de Sitter also spoke of the need to suppose that space is filled with matter, of which the total mass is so enormously great, that compared with it, all matter known to us is utterly negligible. He said “this hypothetical matter I will call the ‘world-matter’”. Even more interestingly he said “in the system A, the world-matter is the three-dimensional space, or at least is inseparable from it”. System A is where “the velocity of light is variable”. He also said “the constant σ only serves to satisfy a philosophical need felt by many, but it has no real physical meaning”. All this is great stuff. Unfortunately in the next breath he said the constant σ “can be mathematically interpreted as a curvature of space”. I don’t think it can actually. Hence de Sitter’s 1918 paper on the curvature of space looks like a backward step to me. Especially when he talks about a field of pure inertia and spherical space. Inertia is there because the mass of a body is a measure of its energy-content, and light curves when space is inhomogeneous. But no matter, there’s some good stuff there for 1918, and we do end up with the de Sitter universe:
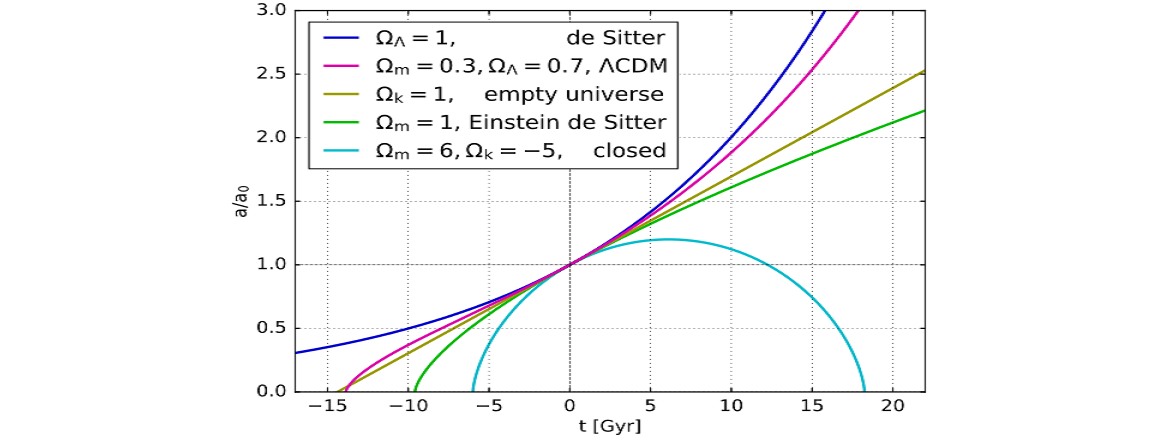CCASA image by Geek3, see Wikipedia
The de Sitter universe “models the universe as spatially flat and neglects ordinary matter, so the dynamics of the universe are dominated by the cosmological constant, thought to correspond to dark energy in our universe”. Since ordinary matter is thought to comprise only 4% of the mass-energy of the universe, what’s not to like?
Schrödinger’s cosmic pressure
Something else to like is Erwin Schrödinger’s cosmic pressure. See the 2014 Cambridge companion to Einstein by Michel Janssen and Christoph Lehner: “Schrödinger [1918] had pointed out another way of treating the cosmological constant: moving it from the left-hand side of Equation [7], where it represents a contribution to space-time curvature, to the right-hand side, where it represents a contribution to the energy-matter distribution. Then it would correspond physically to a kind of cosmic pressure”. Unfortunately Einstein didn’t like it. “In his response to Schrödinger, Einstein [1918d] wrote that he had considered his option too, but had rejected it as artificial”. You can read more in Alex Harvey’s 2012 paper How Einstein Discovered Dark Energy. He gives a translation of Schrödinger’s paper and refers to Einstein’s response: Comment on Schrödinger’s Note ‘On a System of Solutions for the Generally Covariant Gravitational Field Equations’. Schrödinger talked about an energy tensor with vanishing off-diagonal components. The only components that mattered were those in the energy-pressure diagonal. He also talked about a continuous compressible fluid, with a pressure and a density. He also talked about a negative pressure, a tension. It’s pretty much spot on when compared with modern cosmology. See for example what Robert Lambourne says:
Fair use excerpt from Relativity, Gravitation and Cosmology by Robert J Lambourne, see page 252
Also see the 2016 New Scientist article space is full of gigantic holes that are bigger than we expected. It’s by Joshua Sokol, who says “we had to wait until the 1998 discovery of dark energy: a cosmic pressure that forces empty regions of space to expand as if someone was blowing air into each of the universe’s soap bubbles all at once”. Why Einstein thought of this sort of thing as artificial in favour of a closed curved universe I don’t know. Particularly since he was still talking about cosmic pressure in 1919 in a letter to David Hilbert. Particularly since we nowadays think of dark energy as something on the right hand side of the field equation. Particularly since it’s so similar to quintessence, which “differs from the cosmological constant explanation of dark energy in that it is dynamic; that is, it changes over time”. Perhaps Einstein was overly attached to static things.
Friedmann on the curvature of space
Talking of which, see Einstein’s 1917 Static Model of the Universe: A Centennial Review. It’s by Cormac O’Raifeartaigh again, but this time co-authored with Michael O’Keeffe, Werner Nahm, and Simon Mitton. They go through Einstein’s 1917 paper blow by blow. They also give a wealth of history including information on Alexander Friedmann’s 1922 paper on the curvature of space. They also say “few physicists paid attention to Friedmann’s time-varying cosmology, possibly because the work was quite technical and made no connection to astronomy”. They tell how Einstein publicly faulted it, and whilst he retracted his criticism in 1923, “an unpublished draft of Einstein’s retraction demonstrates that he did not consider Friedmann’s cosmology to be realistic”. I dislike Friedmann’s cosmology because I associate spatial curvature with electromagnetism, and don’t like to see spatial curvature in a gravitational context. I also dislike the way in 1924 Friedmann covered all the bases with negative curvature, no curvature, and positive curvature. It’s as if Friedmann has his raisin cake and eats it. As per string theory, if a theory predicts anything, it predicts nothing. But never mind me, check out “The Waters I am Entering No One Yet Has Crossed”: Alexander Friedmann and the Origins of Modern Cosmology. It was written by Ari Belenkiy in 2013 and it’s another interesting historical paper. Belenkiy argues that Friedmann should get credit for the expanding universe as opposed to Georges Lemaître. He also refers to the m-for-monotonic M1 universe which expands from a singularity and has an inflexion point, an M2 universe which expands from a non-zero radius, and a p-for-periodic P universe which expands and contracts. I don’t like point singularities or the Big Bounce, but it’s all grist for the mill.
Lundmark’s Hubble constant
Another interesting historical paper is Who discovered Universe expansion? by Ian Steer dating from 2012. He argues that Knut Lundmark should get the credit for discovering the expanding universe instead of Lemaître. He says Lundmark was the first person to find observational evidence for expansion in 1924, and that his expansion rate was within 1% of the best measurements today. Also see The First Determination of The Hubble Constant by Stephen Kent. Lundmark’s landmark paper was in MNRAS in June 1925 and was called The Motions and the Distances of Spiral Nebulæ.
Lemaître’s expanding universe
Yet another interesting historical paper is Who discovered the expanding universe? It’s by Harry Nussbaumer and Lydia Bieri, and it dates from 2011. They argue that Lemaître should get credit for the expanding universe as opposed to Hubble. Lemaître used galactic redshifts measured by Slipher in 1917 along with distances estimated by Hubble in 1925 and 1926. He put two and two together and concluded that the universe must be expanding. He didn’t mention Slipher directly, he said “utilising the 42 nebulae figuring in the lists of Hubble and of Strömberg”. And that was only in the 1927 French paper. Einstein thought the idea was abominable, but Eddington didn’t. The 1931 English translation is Expansion of the Universe, A Homogeneous Universe of Constant Mass and Increasing Radius Accounting for the Radial Velocity of Extra-Galactic Nebulae. It lacked some crucial paragraphs, and there was a time when this was allegedly due to foul play. However as Mario Livio demonstrated in 2011 in Lost in translation: Mystery of the missing text solved, it was actually Lemaître who omitted them. But regardless, I like Lemaître’s paper because it starts with this: “According to the theory of relativity, a homogeneous universe may exist such that all positions in space are completely equivalent: there is no centre of gravity”. That’s right. A star is surrounded by inhomogeneous space, because inhomogeneous space is what a gravitational field is. So if space is homogeneous on the largest scale, the universe has no overall gravitational field. OK I don’t like what he said about positive curvature, because if space is homogeneous, light goes straight and your pencil doesn’t fall down. But I do like the internal stresses which reduce to a simple pressure which is variable with time. OK I don’t like the way he said this pressure is radiation pressure. But I do like the way he said we have a universe of constant mass. That I like, because I like conservation of energy. I also like the way he said the galactic redshift depends on “the ratio of the radii of the universe at the instants of observation and emission”. And the way the radius of the universe “increases without limit from an asymptotic value R0 for t = –∞”. That I really like, because I really don’t like point singularities. Excellent stuff.
Robertson on relativistic cosmology
Howard Robertson was hard on Lemaître’s heels. See Wikipedia and you can read how “Robertson’s most notable achievements were in applying relativity to cosmology. He developed the concept of an expanding universe, and predicted the redshift, which he plotted using the available data. In 1929, this was confirmed by Edwin Hubble”. Robertson’s 1928 paper was On Relativistic Cosmology. He talked of an “empty world” akin to de Sitter’s universe: “as a whole the irregularities caused by the aggregation of matter into stars and stellar systems may be ignored; and if we further assume that the total matter in the world has but little effect on its macroscopic properties, we may consider them as being determined by the solution for an empty world”. That sounds good. But then he talked about a hypersphere in higher-dimensional 5-space, and about a Euclidean universe of infinite extent, and about interchanging past and future. I found it all rather abstract myself. Ditto for his 1929 paper On the foundations of relativistic cosmology. This is where he allegedly found “all the solutions that describe the cosmological spaces”. However he ended up saying “the world lines of all matter in the universe form a coherent pencil of geodesics”. And that our idealized space-time is a “hypersurface of revolution in a 5-dimensional flat space”. That doesn’t sit well with me, because a world line isn’t something real, nor is a geodesic, and nor is a hypersurface. I fear Robertson was getting lost in maths here, and all in all, I am uncertain of his contribution to cosmology.
Hubble’s relation between distance and radial velocity
I feel more certain about Edwin Hubble. He’s generally thought of as the man who discovered the expanding universe. He’s the man the Hubble telescope was named after. The Wikipedia article contains some good history, telling how in 1922-23 he used Cepheid variables to establish that spiral nebulae were so distant they had to be galaxies in their own right. That settled the Shapley-Curtis debate and appeared in the New York Times in 1924. In 1926 he produced a paper on Extragalactic nebulae featuring a wealth of information including some beautiful images of galaxies:
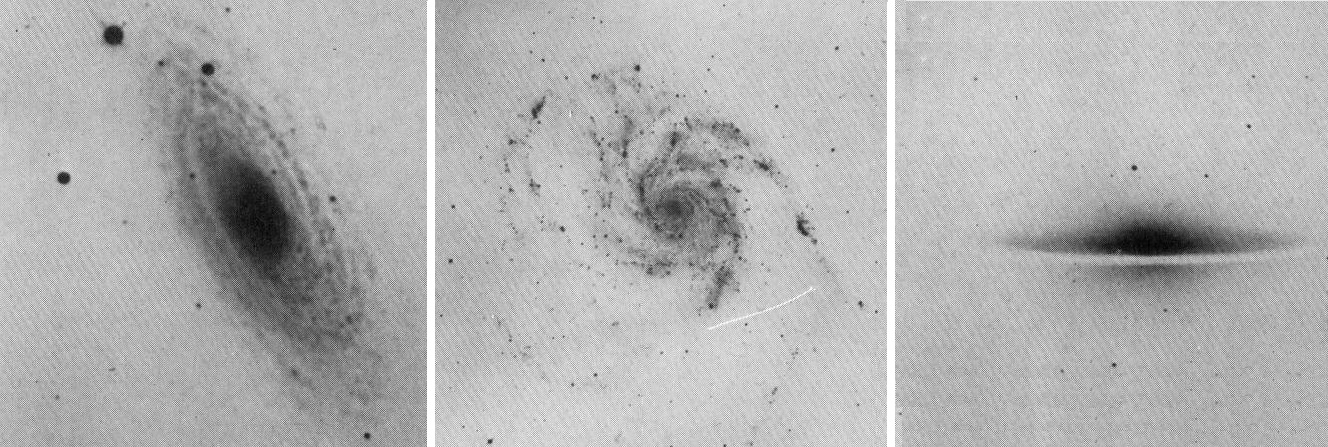Images by Edwin Hubble and the Carnegie observatories
In 1929 Hubble compared galactic distances and redshift: “Combining his measurements of galaxy distances with measurements of the redshifts of the galaxies by Vesto Slipher, and by his assistant Milton L Humason, he found a roughly linear relation between the distances of the galaxies and their redshifts, a discovery that later became known as Hubble’s law”. The title of his paper was a relation between distance and radial velocity among extra-galactic nebulae. However most people don’t appreciate that Hubble credited de Sitter for predicting a “tendency of material particles to scatter”. Or that Hubble was never convinced that the redshift was actually due to the expansion of the universe. As ever it’s all interesting stuff. As is Dismantling Hubble’s Legacy? by Michael J Way dating from 2013. Meanwhile I would urge you to take a look at the Edwin Hubble Bibliography and read the law of the red shifts dating from 1953. Hubble tells the story of cosmic discovery with what I can only describe as humility and awe. He also said this: “When recession factors are included, the distance relation is expected to be linear or non-linear in the sense of accelerated expansion”. Hubble anticipated the discovery of the accelerating expansion of the universe, by as much as seventy years.
The Einstein-de Sitter universe
By 1930 the expanding universe was all the rage. Helge Kragh tells us about de Sitter’s view in Preludes to dark energy: Zero-point energy and vacuum speculations. He says de Sitter believed the cosmological constant was responsible for the expansion of space, and quotes him saying this: “It is the presence of lambda, the ‘cosmological constant’ of Einstein, in the equations that not only closes up the universe, … but also provides the possibility of its changing its size”. Kragh includes a cartoon of de Sitter as a lambda blowing up a cosmological balloon:
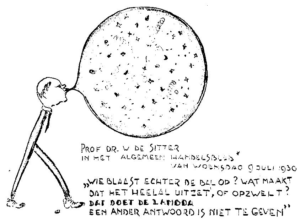Sketch in the Algemeen Handelsblad of 9 July 1930, as reproduced in Peebles (1993 p81). De Sitter says: “What, however, blows up the ball? What makes the universe expand or swell up? That is done by lambda. No other answer can be given”.
However a year later lambda was gone. That was when Einstein agreed that the universe was expanding. See Einstein’s conversion from his static to an expanding universe written by Harry Nussbaumer in 2013. Also see Einstein’s cosmology review of 1933: a new perspective on the Einstein-de Sitter model of the cosmos. It was written in 2015 by the Cormac O’Raifeartaigh, Michael O’Keeffe, Werner Nahm, and Simon Mitton team. They refer to a variety of cosmic models proposed in the early 1930s: “Eddington 1930, 1931: de Sitter 1930a, 1930b; Tolman 1930a, 1930b, 1931, 1932; Heckmann 1931, 1932; Robertson 1932, 1933”. They also refer to “the Friedmann-Einstein model of 1931 and the Einstein-de Sitter model of 1932”, and they point out that the Einstein-de Sitter paper was extremely short. It was On the relation between the expansion and the mean density of the universe and it was only two pages long. Hence they were “delighted” to find a review by Einstein containing “a detailed exposition of the Einstein de Sitter model”. They give a guided tour starting on page 7 and a translation starting on page 40. The bottom line is that Einstein abandoned his cosmological constant in 1931, then abandoned the curvature in 1932. The resulting Einstein-de Sitter universe remained a favoured model of the universe for many years.
Lemaître gets noticed
Meanwhile Lemaître was having his annus mirabilis. In 1931 the English translation of Expansion of the Universe, A Homogeneous Universe of Constant Mass and Increasing Radius Accounting for the Radial Velocity of Extra-Galactic Nebulae appeared in MNRAS. 1931 was also when The Beginning of the World from the Point of View of Quantum Theory appeared in Nature. It’s not even half a page, but it introduced the idea of the universe starting out as a “unique atom, the atomic weight of which is the total mass of the universe”. He also wrote The Expanding Universe which appeared in MNRAS in 1931. His paper Discussion on the Evolution of the Universe appeared in Nature later that year. He said “pressure is the chief factor in the question of instability of a static universe. If the pressure was rigorously zero, the expansion would never occur”. He also talked about condensation and cosmic rays and the formation of a star from an atom. He went on to say this: “at the origin, all the mass of the universe would exist in the form of a unique atom: the radius of the universe, although not strictly zero, being relatively very small. The whole universe would be produced by the disintegration of this primeval atom“. He elaborated in 1933 in a paper entitled Evolution of the Expanding Universe. He talked of the cosmological constant in terms of a pressure related to vacuum energy density: “In order that absolute motion, i.e., motion relative to vacuum, may not be detected, we must associate a pressure p = – ρc² to the density of energy ρc² of vacuum. This is essentially the meaning of the cosmical constant λ”. He also talked of an accelerating expansion: “the motion in the idealized model is of the ever-expanding type: a retarded expansion passing through a minimum velocity at some time t, when the total gravitation force vanishes, and expanding again under the predominant effect of the cosmical repulsion, the velocity tending finally to infinity”. Lemaître anticipated the discovery of the accelerating expansion of the universe by sixty five years, but was somehow sidelined.
Back with a bang
Soon thereafter in 1936 Arthur Walker wrote On Milne’s theory of world-structure, and the Friedmann–Lemaître–Robertson–Walker metric was born. The prehistory of dark energy then entered something of a steady state. In less than twenty years Einstein had invented his cosmological constant and abandoned it, along with Schrödinger’s cosmic pressure. Meanwhile Lemaître got noticed, but not enough. Hence in 1998 the discovery of the accelerating expansion of the universe came as a surprise. The cosmological constant is now back with a bang, but now with an important difference. We’re now seeing papers like Dynamical dark energy: scalar fields and running vacuum. It’s by Joan Sola, Adria Gomez-Valent, and Javier de Cruz Perez, and it was written in 2016. They say the “the current cosmological data disfavors the hypothesis Λ=const in a rather significant way”. They’re talking about a cosmological constant that, like the fine-structure constant, isn’t constant. Their last word is that dark energy density is decreasing with the expansion of the universe, and thus dark energy behaves as a quintessence.
Quintessence
It’s a funny old world. What goes round comes round. Because it isn’t just the cosmological constant that’s been resurrected. I forgot to mention just how far back dark energy goes. Or that Helge Kragh tells us that pre-quantum and pre-relativity analogies to dark energy date back to the nineteenth century. He says this: “the general idea that cosmic space is permeated by an unusual form of hidden energy – a dark energy of some sort – was popular during the Victorian era, where space was often identified with the ether”. He goes on to describe how some “assumed that it was quasi-material and only differed in degree from ordinary matter”. He later talks about Einstein’s resurrection of the ether: “Einstein began to speak of physical space, as described by the metrical tensor gμν in his general theory of relativity, as an ‘ether’”. Kragh also talks about Einstein delivering a lecture in Nottingham in 1930. That’s where Einstein said space “has in the last few decades swallowed ether and time and also seems about to swallow the field and the corpuscles, so that it remains the sole medium of reality”. This is true. Something else that’s true is that the ancient Greeks thought the moon and other heavenly bodies were made of pure incorruptible quintessence. Quintessence is the fifth essence. The fifth element. Quintessence is the aether. The aether is back. With a bang. A big bang. Talking of which…