Quantum electrodynamics

Quantum electrodynamics arguably goes back to Werner Heisenberg and Wolfgang Pauli in 1929, when it was the same thing as quantum field theory. But as pointed out by Robert Oppenheimer in 1930, it suffered from the “divergence issue”, also known as the “problem of infinities”. So much so that some historians say most workers in the field doubted its correctness, and some say the accepted wisdom was that it was no good. Others say physicists were overwhelmed by the problems and believed that a conceptual change was needed. Jagdish Mehra and Helmut Rechenberg talk about the situation in the conceptual completion and the extensions of quantum mechanics 1932-1941. They say at the start of the 1940s quantum field theory was still plagued by the infinities, but that “three theoretical physicists – separated from each by vast distances, with no mutual personal acquaintance or awareness of each other’s existence – sought to improve upon this situation”.

Stueckelberg the forerunner

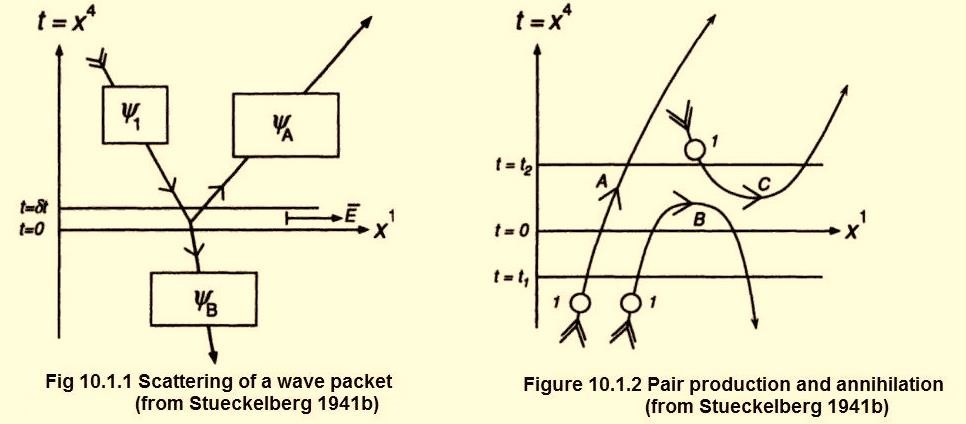
The first of the three was Ernst Stueckelberg, sometimes described as a forerunner of modern physics. In 1934 he’d written a paper on the Relativistic invariant perturbation theory of the Dirac electron. However it was not adopted by others at the time, which was said to be very unfortunate. In 1938 he’d written a three part paper on the forces of interaction in electrodynamics and in the field theory of nuclear forces. However it didn’t get much attention. In 1941 he presented a paper in Basle on the significance of proper time in wave mechanics, then followed up with two further papers the following month, one of which included Stueckelberg diagrams:

Stueckelberg diagrams from Silvan Schweber’s QED and the men who made it, page 576

Mehra and Rechenberg say Stueckelberg “considered the process of electron-positron pair creation and annihilation which could be visualized in a space-time diagram: the positron appeared like an electron running back in time”. This is nowadays known as the Feynman-Stueckelberg interpretation. Time is not something we move through, either forwards nor backwards, so this interpretation is incorrect. However there is a sense in which a positron really is a “time-reversed” electron. We’ll come back to that another day. Meanwhile I note that in his Nobel lecture Feynman said he stole the idea of representing positrons as electrons going back in time from his advisor John Wheeler. I also note the popular legend that when Feynman, Schwinger, and Tomonaga were exiting the stage at the Nobel ceremonies, Schwinger quipped, “By the way Dick, professor Stueckelberg wants his lecture notes back”. That’s perhaps a veiled reference to Stueckelberg’s lost paper. You can read about it in various places including the St Andrews Stueckelberg biography written by John O’Connor and Edmund Robertson. They say in the early 1940s Stueckelberg “wrote a long paper outlining a complete and correct description of the renormalization procedure for quantum electrodynamics. He sent it to the Physical Review, but it was rejected”. You can also read Jagdish Mehra quoting Feynman saying Stueckelberg “did the work and walks alone toward the sunset; and, here I am, covered in all the glory, which rightfully should be his”. On Woit’s website and elsewhere you can read that Stueckelberg’s paper might have been floating around the USA physics community for years. It all sounds so promising, but on the down side see page 578 of Silvan Schweber’s QED and the men who made it. That’s where Schweber said Stueckelberg eventually “accepted Dirac’s (1938b) philosophy that considered electrons pointlike”. For me, point particles disappoint. Schweber also said Stueckelberg extended Dirac’s subtraction procedure and derived divergence-free equations of motion for point charges. He referred to Stueckelberg’s 1944 Nature paper describing an unambiguous method of avoiding divergence difficulties in quantum theory.

Feynman and Tomonaga soldier on

Mehra and Rechenberg also talk about Richard Feynman and his 1942 thesis on the principle of least action in quantum mechanics. They say Feynman had no faith in Wheeler’s programme to solve the outstanding problems of quantum electrodynamics. That’s because the classical part of the theory written by Wheeler resisted all efforts at renormalization. Hence Feynman “pursued the work on his thesis along a different path”. He learned from Herbert Jehle that Paul Dirac had proposed a scheme to replace the usual Hamiltonian formulation of quantum field theory by a Lagrangian formulation, and thought that this offered promise. But soon Feynman was recruited to the Manhattan project, and QED was off his agenda. Mehra and Rechenberg say another theoretical physicist seeking to improve the situation was Sin-Itirô Tomonaga in Tokyo. Tomonaga tells his story in his Nobel lecture. He said Dirac’s 1932 paper on relativistic quantum mechanics attracted his interest because of the novelty of its philosophy and “the beauty of its form”. After investigation he found that it was mathematically equivalent to the older Heisenberg-Pauli theory. He said Dirac treated electrons “according to the particle picture” whilst they were “treated as waves in the Heisenberg-Pauli theory”, but the latter was not relativistically covariant. Tomonaga said Hideki Yukawa wrote a paper in 1942 emphasizing this unsatisfactory aspect, and thought it should be possible to do something about it. He said the first phenomenon which attracted his attention was the electromagnetic mass of the electron. He said the electron “produces an electromagnetic field around itself. In turn, this field, the so-called self-field of the electron, interacts with the electron”. And that because of this, the apparent mass of the electron differs from the original mass, the excess mass being the electromagnetic mass. Tomonaga said according to Weisskopf’s 1939 paper on the self-energy and the electromagnetic field of the electron, this electromagnetic mass turned out to be infinite, which was of course contrary to experiment. He also said “In order to overcome the difficulty of an infinitely large electromagnetic mass, Lorentz considered the electron not to be point-like but to have a finite size. It is very difficult, however, to incorporate a finite sized electron into the framework of relativistic quantum theory”. See Tomonaga’s paper on a relativistically invariant formulation of the quantum theory of wave fields. It was written in Japanese in 1943, and translated into English in 1946. Part II was co-authored with Zirô Koba and Takao Tati in 1946:

Fair usage expert from  on a relativistically invariant formulation of the quantum theory of wave fields II 

Tomonaga said in 1946 Shoichi Sakata wrote a paper proposing a cohesive force field and a new mass which was negative and infinite and thus cancelled out the infinite electromagnetic mass. He also said it was later found that Abraham Pais “proposed the same idea in the U.S. independently of Sakata”. See the brief item on page 796 of physical review volume 70, within the minutes of the meeting of September 19-21, 1946 at New York. Tomonaga asked himself whether the electron-scattering infinities could be similarly removed, and said an example of a computation had already been given by Oppenheimer’s student Sidney Dancoff in a 1939 paper on radiative corrections for electron scattering.

Dancoff’s error

Tomonaga said “What we had to do was just to replace the electromagnetic field by the cohesive force field in Dancoff’s calculation”. Tomonaga also said he happened to discover a simpler method of calculation, and that “I mobilized young people around me and we performed the computation together”. They discovered a mistake in Dancoff’s calculation wherein one crucial term had been overlooked. When corrected, the infinities in the scattering process cancelled completely, except for “the divergence of vacuum polarization type”. However, Tomonaga said Dancoff had already discovered that the latter could be amalgamated into an apparent change in the electron charge, and that there are no other divergences in the theory. Tomonaga also said when a theory is incompetent in part, it is a common procedure to rely on experiment for that part, and this procedure is called the renormalization of mass and charge. He said the word renormalization was in Dancoff’s paper, and “his error was very unfortunate; if he had performed the calculation correctly, the history of renormalization theory would have been completely different”.

The Shelter Island conference

That history includes the famous Shelter Island conference. It was a three-day event lasting from the evening of Sunday 1^st June 1947 through to Wednesday evening, and intended to emulate the Solvay conferences in Europe. You can read all about it in Silvan Schweber’s 2011 Shelter Island revisited:

Photograph from the AIP Emilio Segrè Visual Archives, Marshak Collection

Schweber tells how on the final part of the 100-mile trip from New York, the conference bus was accompanied by a police motorcycle escort, and in Greenport the attendees were wined and dined by the local Chamber of Commerce. In an after-dinner speech, a grateful chamber president John C White said he’d been a Marine in the Pacific, and that he and many like him would not be alive were it not for the atomic bomb. Schweber also said the timing was “to accommodate the presence of Oppenheimer, who was also to write a 500-word paper outlining subjects for discussion. The other two physicists asked to prepare papers for the conference were Victor Weisskopf and Hendrik Kramers”. Oppenheimer’s paper concentrated on cosmic-ray phenomena, Weisskopf’s paper outlined the problems facing particle physics, and “Kramers, for his part, chose to review the difficulties encountered in QED since its inception in 1927 and to indicate one way out of these problems”. Schweber described how Kramers referred to his own work of 1938–1940, and the work of his students Jean Serpe and Wladyslaw Opechowski which described “how an electron with experimental mass behaves in its interaction with the electromagnetic field”.

Oppenheimer was in absolute charge and impressive

Schweber also said Karl Darrow chaired the conference, but Oppenheimer was the dominant personality who was “in absolute charge” and impressive. He said the next most impressive was Bethe, and that on the first day of the conference Willis Lamb presented data from his experiment with Robert Retherford. They’d measured what’s now known as the Lamb shift, the unexpected difference between the 2s½ and 2p½ energy levels of the hydrogen atom. See their paper fine structure of the hydrogen by a microwave method. Lamb’s presentation was followed by Isidor Rabi, who presented data on the hyperfine structure of hydrogen and deuterium. See his paper co-authored with John Nafe and Edward Nelson. The next morning Kramers gave his QED review, which was “clearly influential”. In the afternoon Weisskopf “reviewed the divergence difficulties in the hole-theory calculations of the self-energy of an electron”. Schweber said during the ensuing discussion, Weisskopf and Schwinger indicated how a hole-theoretic calculation of the level shift might be attempted. Schweber also said Bethe performed his famous non-relativistic calculation on the train ride home from New York to Schenectady. Amazingly enough, hole theory was still around in 1947.

The Bethe-Lewis scheme

On page 195 of his 1997 book conceptual development of 20th century field theories, Tian Yu Cao talks about the Bethe-Lewis scheme for mass renormalization. He says “soon after the discovery of the level shift of hydrogen by Lamb and Retherford (1947) with the microwave method, Bethe accepted a suggestion by Schwinger and Weisskopf and tried to explain the interaction of the electron and the radiation field”. He says Bethe pointed out that it was possible to identify the most strongly divergent term with an electromagnetic mass effect, which should be regarded as already included in the observed mass of the electron. Cao goes on to say that inspired by Bethe’s success, Harold Warren Lewis “applied the mass renormalization procedure to the relativistic calculation of the radiative correction to the scattering cross section”. And that in doing so, Lewis made the nature of the renormalization clearer by claiming that “the electromagnetic mass of the electron is a small effect, and that its apparent divergence arises from a failure of present day quantum electrodynamics above certain frequencies”. Bethe’s 1947 paper was on the electromagnetic shift of energy levels. It was received by Physical Review on June 27^th and published on the 15^th August. Lewis’s paper was on the reactive terms in quantum electrodynamics, It was received by Physical Review on 24th November and published on 15^th January 1948. Cao says Lewis combined the assumed-to-be-small electromagnetic mass with a finite “mechanical” mass to obtain an observed mass, then subtracted the electromagnetic mass. He also says “in this way the renormalization procedure had obtained a solid physical ground”. Renormalization had achieved “a solid physical ground” by adjusting the electron mass from infinity to 511lkev/c², via a retrofit to an experimental result. There is no understanding of the electron here.

Tomonaga’s papers

While all this was going on Tomonaga was busy. He presented a preliminary account of his work at the Kyoto symposium in November 1947. See page 609 of climbing the mountain: the scientific biography of Julian Schwinger by Jagdish Mehra and Kimball Milton. They say at the end of 1947, Tomonaga was in full possession of the concepts of charge and mass renormalization. They refer to Progress of Theoretical Physics 2 217 (1947). This was Tomonaga’s correction due to the reaction of “cohesive force field” for the elastic scattering of an electron co-authored with Daisuke Ito and Zirô Koba. Perhaps Mehra and Milton meant to refer to application of the “self-consistent” subtraction method to the elastic scattering of an electron by Tomonaga and Koba, received on 1^st November 1947 and published on 1^st December. However Mehra and Milton say Tomonaga communicated his results on elastic electron scattering on 30^th December, the same day Schwinger sent in his paper on the anomalous magnetic moment of the electron.

Schwinger stakes his claim

Silvan Schweber tells the Schwinger story starting on page 316 of QED and the men who made it. He starts with Schwinger’s motivational discussion with Norman Ramsey in September 1947. Schwinger then set to work, then in November went to a conference in Washington and gave a status report that “got Oppy very excited”. That’s because Schwinger had indicated that “the discrepancy in the hyperfine structure of the hydrogen atom… could be explained on the same basis as that of the electromagnetic self-energy, as can the line shift of Lamb”. Schweber says in doing this “Schwinger had transformed the perception of quantum electrodynamics, and had made it into an effective, coherent, and consistent computation scheme to order e²”. The news spread rapidly. Rabi said “God is great”, and Bethe said Schwinger’s theory was wonderful, even though “nobody so far has been able to give me a complete account of his theory”. Schwinger’s paper was on quantum-electrodynamics and the magnetic moment of the electron. It was received by Physical Review on 30^th December 1947 and published on 15^th February 1948. At one page, it is short. Schwinger said the simplest example of radiative correction is for an electron in a magnetic field. And that “the detailed application of the theory shows that the radiative correction corresponds to an additional magnetic moment associated with the electron spin of magnitude δμ/μ = (½π)e²/ħc = 0.001162. It is indeed gratifying that recently acquired experimental data confirm this prediction”. He said prediction even though it was a postdiction. He also said “a paper dealing with the details of this theory and its applications is in course of preparation”. There’s a definite feeling here that Schwinger was staking a claim to establish priority. Especially since Mehra and Milton say Schwinger said his relativistic calculation of the Lamb shift was consistent with that of Bethe, but that “the vagueness of the latter remark reflected Schwinger’s awareness that his calculation was wrong”. Elsewhere they refer to “a characteristic Schwinger patent application”. Nevertheless, Schwinger had struck gold.

Schwinger strikes gold

Schweber tells how at the New York APS meeting, Schwinger’s lecture was recent advances in quantum electro-dynamics, given on January 31^st 1948. He says Karl Darro noted that it was “given too rapidly for my apprehension but given with great gusto which implied a great advance”. Schwinger’s lecture “attracted such a large gathering that it was necessary for him to repeat it”. A young Freeman Dyson said at the end Schwinger “made a dramatic announcement of a still newer and more powerful theory which is still in embryo”, and “there were tremendous cheers when he announced that the crucial experiment had supported his theory”. Schwinger’s first presentation of his covariant formulation was at the Pocono conference on March 31^st 1948. It lasted most of the day. There’s an account of it by James Gleick in his 1992 book Genius. See page 256. Gleick tells how Schwinger stressed that this theory of quantum electrodynamics met the dual criteria of relativistic invariance and gauge invariance. It was a theory where “each small volume of space is now to be handled as a particle”. Schwinger introduced a difficult new notation and set about to derive a sampling of specific results. However “if his distinguished listeners found themselves in darkness, they were nevertheless not so easily cowed as Schwinger’s customary audiences, and the usual express train found itself halted by interruptions”. Gleick says Bohr himself broke in with a question, but Schwinger cut him off. He also says Bethe noticed that the formal mathematics silenced the critics, who raised question only when Schwinger tried to express physical ideas. And that “Fermi, glancing about at his famous colleagues, noticed with some satisfaction that one by one they had let their attention drift away. Only he and Bethe had managed to stay with Schwinger to the end”.

Schwinger was the next Einstein

Nevertheless as Jagdish Mehra said, the conference belonged to Schwinger. And as Hans Bethe said, Schwinger’s theory was closely connected to the known quantum electrodynamics, so Niels Bohr was convinced it was correct. Schwinger’s fame grew, so much so that after he gave an APS lecture in Pasadena in June 1948, the New York Times reportage was hyperbolic. They said SCHWINGER STATES HIS COSMIC THEORY; Physicists Awed as Harvard man of 30 Tells Version of Electrodynamic Forces. They also said “the new theory was presented by Dr Julian Schwinger, whom American physicists regard as the heir-apparent to the mantle of Einstein”. Schwinger’s paper quantum electrodynamics I : a covariant formulation was received on July 29^th 1948 and published on 15^th November. He said “attempts to avoid the divergence difficulties of quantum electrodynamics by mutilation of the theory have been uniformly unsuccessful”. He also said “we inquire whether quantum electrodynamics can account unambiguously for the recently observed deviations from the Dirac electron theory, without the introduction of fundamentally new concepts”. Only he talked of the proper mass of the photon, and the charge fluctuations of the vacuum. So I don’t think he had any concept of what mass is, or what charge is. He also talked of the electromagnetic field and the matter field. So I don’t think he had any concept of the what a photon is, or what an electron is. And yet you can read that “as Schwinger stood at the blackboard, writing ambidextrously and speaking mellifluously in well-formed sentences, it was as if God Himself was handing down the Ten Commandments”. That’s in Schwinger: the forgotten genius of physics by Rodney Brooks. As is this: “I believe that the main reason these masterpieces have been ignored is that many physicists found them too hard to understand. (I know one who couldn’t get past the first page)”. One can’t help thinking of the Emperor’s New Clothes. Even Schwinger’s Nobel lecture is dripping with maths.

Feynman’s fail

Feynman was different. He had a head start with his 1942 thesis, but with his wartime stint at Los Alamos, he lost ground. Then when quantum electrodynamics fired up again, he had a bad start. James Gleick gets it across in Genius, see page 257. He says at the January APS meeting in New York, Oppenheimer was smoking his pipe on the front row, and Schwinger was the star. When Schwinger repeated his lecture by popular demand, “Feynman rose during the question period to say he too had reached these results and that, in fact, he could offer a small correction. Immediately he regretted it. He thought he must have sounded like a little boy piping up with “I did it too, Daddy””. Gleick says “few people that winter realized the depths of rivalry he felt”. Things did not improve at the Pocono conference in March. Feynman’s presentation came after Schwinger’s marathon performance, and he didn’t stick to plan. That’s because his mentor Hans Bethe had suggested that Feynman follow Schwinger’s example and take a mathematical approach to his presentation. Gleick says Schwinger was hearing Feynman’s theory for the first time, thought it intellectually repulsive, and “could see that Feynman was offering a patchwork of guesses and intuition”. Gleick also says Bethe interrupted Feynman, sensing the audience was numbed with detail, and tried to return Feynman to fundamentals. Feynman “explained his path integrals, an alien idea, and his positrons moving backwards in time, even more disturbing”. Gleick says Edward Teller caught the apparent infringement of the exclusion principle, and refused to accept Feynman’s unrigorous justification. When Dirac asked if the theory was unitary, Feynman didn’t even know what he meant. Then when Feynman drew his diagrams on the blackboard “Bohr rose to object. Had Feynman ignored the central lesson of two decades of quantum mechanics? It was obvious, Bohr said, that such trajectories violated the uncertainty principle. He stepped to the blackboard, gestured Feynman away, and began to explain”.

QED Feynman diagrams from Rod Nave’s hyperphysics

Bohr continued for long minutes, and Feynman knew he had failed. Gleick says at the time Feynman was in anguish. He says Feynman was in runner-up vein when he was asked to help select a winner for a National Academy of Sciences prize. And that “when Schwinger saw Feynman’s name on the list of judges, he inferred correctly that the prize was meant for him”.

Dyson makes a difference

Gleick tells how Oppenheimer was impressed by Schwinger and unimpressed by Feynman, all the more so because “awaiting him back in Princeton was a startling confirmation of Schwinger’s theory”. It was a letter from Tomonaga plus a collection of manuscripts. Oppenheimer telegraphed back encouraging him to write a summary of his work, which he would arrange to have published in Physical Review. This was a paper on infinite field reactions in quantum field theory. It made its mark on Freeman Dyson. He was also in Princeton, and as Gleick says, “the revelation of Tomonaga’s papers lay in what seemed a simple beauty. He thought that he now understood Schwinger and that not all Schwinger’s complications were necessary”. Gleick also says graduate students poring over the Pocono notes already suspected this, despite the acclaim their elders were awarding. And that “Dyson quoted “an unkind critic” as having said “Other people publish to show how to do it, but Julian Schwinger publishes to show you that only he can do it”. He seemed to strive for an exceptional ratio of equations to text”. Gleick goes on to talk about Dyson’s June 1948 road trip with Feynman to Albuquerque. Dyson was on his way to Ann Arbour in Michigan to hear Schwinger give a series of lectures, but “relished the chance to spend time with Feynman. No one interested him so much”. Dyson said he knew that somewhere hidden in Feynman’s ideas was the key to a theory of QED that was simpler and more physical than Julian Schwinger’s elaborate construction. That autumn Dyson finished his paper on the radiation theories of Tomonaga, Schwinger, and Feynman:

Fair use excerpt from the radiation theories of Tomonaga, Schwinger, and Feynman

It was received on 6^th October 1948 and published on 1^st February 1949. Dyson said “a unified development of the subject of quantum electrodynamics is outlined, embodying the main features both of the Tomonaga-Schwinger and of the Feynman radiation theory”. And that “the chief results obtained are a) a demonstration of the equivalence of the Feynman and Schwinger theories, and b) a considerable simplification of the procedure involved in applying the Schwinger theory to particular problems”. He referred to the 1946 translation of Tomonaga’s 1943 paper on a relativistically invariant formulation of the quantum theory of wave fields, and to Tomonaga’s 1947 case of interacting electromagnetic and electron fields co-authored with Zirô Koba and Takao Tati. He also referred to Tomonaga’s 1948 case of interacting electromagnetic and meson fields co-authored with Suteo Kanesawa, and to Tomonaga’s 1948 paper on infinite field reactions in quantum field theory. Dyson said several papers giving a complete exposition of Schwinger’s theory are in course of publication, and little of Feynman’s theory is yet published. The only Schwinger material he referred to was the one-page paper and the paper entitled quantum electrodynamics I : a covariant formulation. The only Feynman material he referred to was a paper on the space-time approach to non-relativistic quantum mechanics and a paper on the relativistic cut-off for quantum electro-dynamics. Dyson had told Bethe that it was Schwinger’s and Feynman’s own fault that they hadn’t published “any moderately intelligible account”, and that by publicising their work he was performing a service to humanity. As to whether he was, is debateable. But Gleick says “the distinctions he drew and the characterizations he set down soon became the community’s conventional wisdom: that Schwinger’s and Tomonaga’s approach was the same, while Feynman’s differed profoundly; and that Feynman’s method was original and intuitive, while Schwinger’s was formal and laborious”.

Dyson and Bethe convert Oppenheimer

Oppenheimer had been waxing lyrical about “Schwinger’s theory” and “Schwinger’s program”, but Dyson begged to differ. In an inter-office memo to Oppenheimer he said “I disagree rather strongly with the point of view expressed in your Solvay Report” and “I am convinced that the Feynman theory is considerably easier to use, understand, and teach”. As a result Oppenheimer set up a series of forums attended by Bethe and others. Gleick says “in the end Bethe turned Oppenheimer around. He cast his vote explicitly with the Feynman theory and let the audience know he felt Dyson had more to say. He took Oppenheimer aside privately, and the mood shifted. By January, the war had been won”. By then Dyson also had a handwritten note saying “Nolo contendere. R. O”. Nolo contendere means no contest. Oppenheimer later rewarded Dyson with a lifetime appointment at the IAS in Princeton. While all this was going on, Tomonaga had written a paper on a self-consistent subtraction method in the quantum field theory co-authored with Takao Tati. It was received on 23^rd May 1948 and published on 1^st December 1948. It was followed by parts II-1 and II-2 in 1949 co-authored with Bunrika Daigaku, Hiroshi Fukuda and Yonezi Miyamoto. But by then Tomonaga had been left behind.

A crossbow in a world of sticks and clubs

By the end of January 1949 Feynman realized he was ahead. He was at the New York APS meeting and heard that “Oppenheimer had devastated a physicist named Murray Slotnick, who had presented a paper on meson dynamics”. Slotnick had been talking about pseudoscalar coupling and pseudovector coupling. The former gave finite answers, the latter didn’t. Oppenheimer had stood up and said “What about Case’s theorem?” He said it proved that the two types of coupling would give the same result, and Case was going to demonstrate this the next day. Feynman went back to his hotel room and calculated that the couplings were not the same. The next morning “he buttonholed Slotnick to check the answer. Slotnick was nonplussed. He had just spent six intensive months on this calculation; what was Feynman talking about? Feynman took out a piece of paper with a formula written on it. Slotnick asked “What’s that Q in there?” Feynman said that was the momentum transfer, a quantity that varied accordingly to how widely the electron was deflected”. Gleick says this was another shock for Slotnick: “here was a complication that he had not dared to confront in a half-year of work. The special case of no deflection had been challenge enough. There was no problem, Feynman said. He set Q equal to zero, simplified his equation, and found that indeed his night’s work agreed with Slotnick. He tried not to gloat, but he was afire. He had completed in hours a superior version of a calculation on which another physicist had staked a major piece of his career. He knew he now had to publish. He possessed a crossbow in a world of sticks and clubs”.

Feynman defines the start of the modern era

Meanwhile Schwinger wrote a paper quantum electrodynamics II : vacuum polarization and self-energy which was published in April 1949. He also wrote a paper quantum electrodynamics III : the electromagnetic properties of the electron—radiative corrections to scattering which was published in September 1949. But Schwinger found the spotlight sliding away, whilst Feynman’s star was rising. Feynman and Dyson were at the Oldstone conference in April 1949 “where the main talking-point was Richard Feynman’s approach to quantum electrodynamics”. Gleick says Feynman published an extended set of papers that defined the start of the modern era. In 1948 Feynman wrote a paper about a relativistic cut-off for classical electrodynamics, a paper about a relativistic cut-off for quantum electrodynamics, and a paper called the theory of positrons. In 1949 he wrote a paper on a space-time approach to quantum electrodynamics. In 1950 he wrote a paper on the mathematical formulation of the quantum theory of electromagnetic interaction. In 1951 he wrote a paper on an operator calculus having applications in quantum electrodynamics. Gleick says “the younger theorists who devoured them realized that Dyson had given only a bare summary of Feynman’s vision. They felt invigorated by his images – beginning with the unforgettable bombardier metaphor in the positron paper – and by his way of insisting on the plainest statements of physical principles in physical language”.

Houston we have a problem

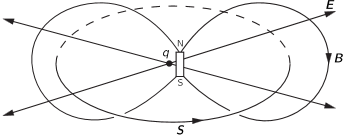
However if you’ve ever actually read any of these papers, you’ll know there’s a problem. On page 5 of his 1948 paper about a relativistic cut-off for classical electrodynamics Feynman said “the rest mass particles have is simply the work done in separating them against their mutual attraction after they are created”. It absolutely isn’t. Feynman was allegedly the leading physicist of his generation, the man with the key to the universe, but he didn’t understand E=mc². He didn’t know that the mass of a body is a measure of its energy-content. It gets worse, because in 1948 Feynman was still saying a positron is an electron going back in time. He didn’t know what a positron was, because he didn’t know what an electron was. In 1963 he still didn’t know. Have you ever read the Feynman Lectures? Take a look at what Feynman said in lecture 27: field energy and momentum:

Feynman lectures Fig. 27–6. Caption: a charge and a magnet produce a Poynting vector that circulates in closed loops

He said this: “Suppose we take the example of a point charge sitting near the center of a bar magnet, as shown in Fig. 27–6. Everything is at rest, so the energy is not changing with time. Also, E and B are quite static. But the Poynting vector says that there is a flow of energy, because there is an E × B that is not zero. If you look at the energy flow, you find that it just circulates around and around. There isn’t any change in the energy anywhere – everything which flows into one volume flows out again. It is like incompressible water flowing around. So there is a circulation of energy in this so-called static condition. How absurd it gets!” Yes Dick. How absurd it gets.

NEXT