We can trace black holes all the way back to John Michell in 1783. He’s the man who devised the torsion balance used by Henry Cavendish to determine the mass of the Earth. Michell was something of an expert on gravity. He talked about “dark stars” which were dark “in consequence of the diminution of the velocity of their light”. He also said this: “if there should really exist in nature any bodies, whose density is not less than that of the sun, and whose diameters are more than 500 times the diameter of the sun, since their light could not arrive at us… we could have no information from sight”. I think that was pretty good for 1783. As was this: “if any other luminous bodies should happen to revolve about them we might still perhaps from the motions of these revolving bodies infer the existence of the central ones with some degree of probability”. That’s exactly what we’ve done to establish the existence of a supermassive black hole in the centre of our galaxy.
Sagittarius A*
Check out Sagittarius A*. It’s part of Sagittarius A, which is a radio source in the middle of the Milky Way. Sagittarius A* is arguably the site of an accretion disk or a relativistic jet rather than the central black hole itself, but either way there’s something very small and very massive at the heart of our galaxy. We’re confident of this because of many years of work by many good men and women. Different people have joined and left the various groups over the years, but in 2002 Rainer Schödel, Thomas Ott, Reinhard Genzel, and twenty other authors reported on the orbital motion of star S2 over a ten year period. In 2008 Stefan Gillessan, Frank Eisenhauer, Sascha Trippe, Tal Alexander, Reinhard Genzel, Fabrice Martins, and Thomas Ott published a paper on the orbits of nearby stars over a sixteen year period. Another noteworthy paper is an update on monitoring stellar orbits in the galactic center. It’s dated November 2016, and is by twelve authors mainly from the Max Planck Institute but also from the Racah Institute and Berkeley. It uses a 25-year dataset derived from VLT and Keck observations. There’s more people involved, too many to mention. But also see the animations produced by Andrea Ghez and team at the UCLA Galactic Center Group using Keck datasets:
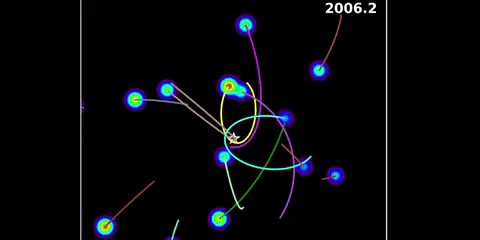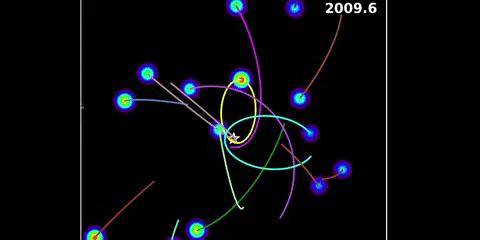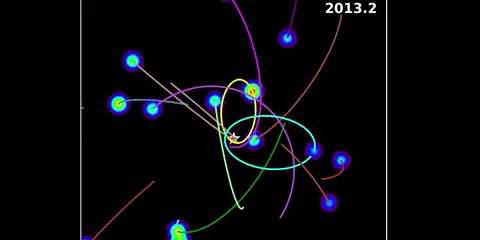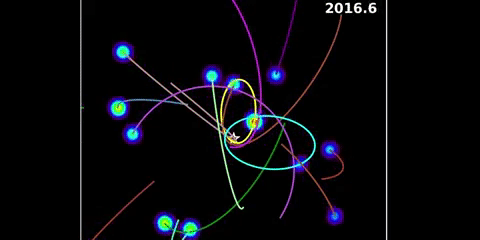Animation by Andrea Ghez and research team at UCLA
There’s something there with a mass that’s circa 4.28 million times the mass of the Sun. But it’s at most thirty times bigger than the Sun in terms of spatial extent. There’s only one thing it can be, and that’s a black hole. Hence we’re confident that black holes exist. As to their exact nature, that’s another story.
The speed of light varies with gravitational potential
The story starts with Einstein saying the speed of light is not constant, and instead varies with gravitational potential. That’s the speed of light in vacuo, which I will shorten to the speed of light. It varies with altitude. Some people will tell you that Einstein said this in 1907 or 1911, then stopped saying it, but he didn’t. He was still saying it in 1913, in 1914, in 1915, in 1916, and in 1920. He never ever stopped saying it. He made it crystal clear that “a curvature of rays of light can only occur in a place where the speed of light is spatially variable”. You can find Irwin Shapiro saying much the same thing in 1964: “according to the general theory, the speed of a light wave depends on the strength of the gravitational potential along its path”. Also see what Don Koks the PhysicsFAQ editor said in 2014: “light travels faster near the ceiling than near the floor”. Hence light curves as per Huygen’s principle, like sonar waves curve downwards when the speed of sound decreases with depth. Matter is similarly affected because of the wave nature of matter. That’s how gravity works. Light doesn’t curve because spacetime is curved. That thing called “curved spacetime” is an abstract thing. It isn’t curved space, it’s a curved “metric”, associated with measurement. It’s effectively a curved plot. A curved plot of measurements of the speed of light made using optical clocks:
Image from Ethan Siegel’s blog starts with a bang
The tidal force at some location relates to the curvature of the plot at that location. This curvature is the second derivative of potential, and is effectively the spacetime curvature or Riemann curvature. The force of gravity at some location relates to the gradient of the plot at that location, the first derivative of potential. The force of gravity is greatest where the gradient is greatest, not where the spacetime curvature is greatest. If there is no gradient, light doesn’t curve and there is no gravity. The tilted light-cones in the Stanford singularities and black holes article are another way of depicting this. Alternatively you can emulate this gradient or tilt with a piece of stiff board. Lift one side up, and roll a marble across it. The path of the marble curves because the board is tilted, not because the board is curved. It’s similar for the room you’re in. The force of gravity is 9.8 m/s² at the floor and at the ceiling, so there’s no detectable tidal force, and so no detectable spacetime curvature. But your pencil still falls down. That’s detectable, as is a difference in NIST optical clock rates. The lower clock goes slower because light goes slower when it’s lower. The bottom line is that the speed of light varies in the room you’re in. If it didn’t, your pencil wouldn’t fall down.
But many physicists say it’s constant
See what David Wineland of NIST says: “if one clock in one lab is 30cm higher than the clock in the other lab, we can see the difference in the rates they run at”. An optical clock goes slower when it’s lower. This is hard scientific evidence for gravitational time dilation. It’s also hard scientific evidence that light goes slower when it’s lower. However despite what Einstein and others said, and despite the hard scientific evidence of optical clocks, many physicists think the speed of light is constant. As to why, I’m not sure. But the Wikipedia variable speed of light article talks about Peter Bergmann who was Einstein’s research assistant in Princeton between 1936 and 1941. He wrote the first textbook on general relativity in 1942. After Einstein died ”Bergmann wrote a new book in 1968 claiming that vector light velocity could change direction but not speed. This has become a prevailing opinion in science”. However that prevailing opinion is wrong, and I’m afraid to say that as a result of that, the nature of black holes is generally misunderstood.
Einstein didn’t believe black holes could form
Einstein wrote a paper on black holes in 1939. It was on a stationary system with spherical symmetry consisting of many gravitating masses. He said “g44 = (1 – μ/2r / 1 + μ/2r)² vanishes for r = μ/2. This means that a clock kept at this place would go at the rate zero. Further it is easy to show that both light rays and material particles take an infinitely long time (measured in “coordinate time”) in order to reach the point r = μ/2 when originating from a point r > μ/2”. That fits with the speed of light being spatially variable. Einstein also said this: “In this sense the sphere r = μ/2 constitutes a place where the field is singular”. He thought of the thing we now call the event horizon as the black hole singularity. That fits with the speed of light reducing to zero. So far so good. But sadly Einstein concluded that “the ‘Schwarzschild singularity’ does not appear for the reason that matter cannot be concentrated arbitrarily”. He said that this was “due to the fact that otherwise the constituting particles would reach the velocity of light”. He said this even though he knew that the material particle falls faster and faster because the speed of light gets slower and slower. If he had ridden his material particle like he rode the light beam he would surely have known that something had to give and predicted gamma ray bursters. Or if he’d recalled his own words about the energy of the gravitational field acting gravitatively he might have sidelined the material particles and focused on light and energy. Then he would surely have been talking frozen-star black holes. Perhaps with Robert Oppenheimer and Hartland Snyder who’d just written their paper on continued gravitational contraction. But this was 1939, a time of Nazis and war, a time when Einstein had somehow lost his confident intuition that had served him so well. It was not to be.
The baby and the bathwater
Twenty years later the “golden age” physicists threw out the baby with the bathwater. See the Wikipedia black hole article where you can read that David Finkelstein identified the Schwarzschild surface as an event horizon, “a perfect unidirectional membrane: causal influences can cross it in only one direction”. The Wikipedia article says “this did not strictly contradict Oppenheimer’s results”, but it did. It utterly contradicted it, and Einstein too. Finkelstein plus Martin Kruskal didn’t say Einstein missed the trick wherein the black hole formed from the inside out. They discarded the Schwarzschild singularity and the frozen star, and the very essence of Einstein’s general relativity. They discarded the speed of light is spatially variable. In doing this they threw out the very reason light curves and why matter falls down. They discarded the very reason the black hole is black. What they discarded, is why doesn’t the light get out?
Why doesn’t the light get out?
It’s one of the simplest questions in cosmology, and one of the most important. But the answer is usually wrong. As for the right answer, imagine you’re standing on a gedanken planet shining a laser beam straight up into space. The light goes straight up. It doesn’t curve, and it doesn’t fall back down. Now imagine it’s a denser more massive planet. The light still goes straight up. It still doesn’t curve, and it still doesn’t fall back down. Let’s make it a really massive planet. That light still goes straight up. It still doesn’t curve, and it still doesn’t fall back down:
Public domain image courtesy of NASA, with light beam added by me
But when we make our gedanken planet so massive that it’s a black hole, all of a sudden light can’t escape. Why? Why doesn’t the light get out? Some will tell you that the light curves back to the event horizon. When you challenge that by saying the light didn’t start curving on the ever-more massive planet, they’ll change tack and say it’s because spacetime is curved. Then when you challenge that by saying light curves because of the gradient rather than the spacetime curvature they’ll change tack again and tell you about the waterfall analogy.
The waterfall analogy
The waterfall analogy is where space is falling inward so the light beam doesn’t make any upward progress. It’s derived from Gullstrand-Painlevé coordinates, which Einstein rejected for good reason. The waterfall analogy may have been publicised on Horizon by Max Tegmark, but it is not in accord with the general theory of relativity. In no sense is space falling inwards in a gravitational field. We do not live in some Chicken-Little world where the sky is falling in. A gravitational field alters the motion of light through space, it doesn’t suck space down into some cosmic plughole. Because as Einstein said in his 1920 Leyden Address a gravitational field is a place where space is “neither homogeneous nor isotropic”. You can find modern authors saying more or less the same thing. See inhomogeneous vacuum: an alternative interpretation of curved spacetime dating from 2008. That’s where Xing-Hao Ye and Qiang Lin talk about the propagation of light in a medium with a graded refractive index. They are essentially correct. We don’t call it gravitational lensing for nothing. Einstein referred to refraction, as did Newton, see Opticks query 20. The contest between Einstein plus Newton versus Chicken Little is no contest at all.
Why the light doesn’t get out
So why doesn’t the light get out? PhysicsFAQ editor Don Koks tells it like it is: “light speeds up as it ascends from floor to ceiling, and it slows down as it descends from ceiling to floor; it’s not like a ball that slows on the way up and goes faster on the way down”. Somewhat counter intuitively, the ascending light beam speeds up, and the descending light beam slows down. Because light goes slower when it’s lower. That’s why optical clocks go slower when they’re lower. So if light goes slower when it’s lower, how much slower can it go? Have a google on infinite gravitational time dilation. What comes up time and time again? Black holes. Gravitational time dilation goes infinite at the black hole event horizon. An optical clock at the event horizon doesn’t tick at all, like Einstein said. And when you understand the nature of time, you know why. It isn’t because some abstract thing called time stops. It’s because light stops. Because the speed of light at the event horizon is zero. That’s why the light doesn’t get out of the black hole. Not because of some mystic curvature that makes vertical light beams bend back round. Not because the sky is falling in. But because at that location, the speed of light is zero. The light isn’t moving, so it doesn’t go up. It doesn’t get out because it is effectively “frozen”. That’s why a black hole is black. Because it’s a frozen star.
Frozen stars
If you google on frozen star and Robert Oppenheimer you can find ample references to the frozen-star black hole. Such as the 1971 Physics Today article introducing the black hole by Remo Ruffini and John Wheeler who said “in this sense the system is a frozen star”. However if you google on frozen star alone, what tends to come up is articles about some new hypothetical stars, or a TV program. Or you get redirected to black holes which feature a central point singularity. It’s like the original “frozen star” has been airbrushed away and replaced with something else. Something that contradicts Einstein but doesn’t say so. At least Andrew Hamilton says so on his JILA website. He says Einstein misunderstood how black holes work and thought the Schwarzschild geometry had a singularity at the event horizon. Hamilton isn’t alone in thinking that. On the Wikipedia Schwarzschild metric article you can read that “the singularity at r = rs is an illusion”, that it’s “an instance of what is called a coordinate singularity”, and that it “arises from a bad choice of coordinates or coordinate conditions”.
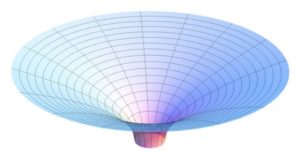Flamm Paraboloid (exterior Schwarzschild solution) CCASA image by AllenMcC, see Wikipedia
I think most physicists would concur with that, and with the Wikipedia article on the propagation of light in non-inertial reference frames. This says “at the event horizon of a black hole the coordinate speed of light is zero”. There’s nothing wrong with that. However the article then says the proper speed is c, and “the local instantaneous proper speed of light is always c”. There’s a problem there of biblical proportions. You can see where it goes in Kevin Brown’s mathpages article the formation and growth of black holes. The article refers to the frozen star interpretation, saying this gives “a serviceable account of phenomena outside the event horizon”. It also says a clock runs increasingly slowly as it approaches the event horizon, and “the natural limit of this process is that the clock asymptotically approaches full stop (i.e., running at a rate of zero). It continues to exist for the rest of time, but it’s frozen”. That fits with Einstein’s thinking, and Oppenheimer’s. However the article favours a “geometrical interpretation” which it incorrectly attributes to Einstein, saying that’s where “all clocks run at the same rate, measuring out real distances along worldlines in curved spacetime”. That’s a surprise given what Einstein said about zero-rate clocks. It’s also a surprise given the hard scientific evidence: NIST can demonstrate two clocks running at different rates when one is a mere 2cm above the other. Hence it contradicts “Einstein and the evidence”. Even more surprising is this: “rather than slowing down as it approaches the event horizon, the clock is following a shorter and shorter path to the future time coordinates. In fact, the path gets shorter at such a rate that it actually reaches the future infinity of Schwarzschild coordinate time in finite proper time”. That’s saying the clock reaches the end of time. And get this: “the object goes infinitely far into the “future” (of coordinate time), and then infinitely far back to the “present”. The clock doesn’t just go to the end of time, it goes to the end of time and back again.
To the end of time and back again
You might be tempted to dismiss Kevin Brown’s mathspages article as some kind of crackpot outlier. Don’t. Because it’s in line with Gravitation by Charles Misner, Kip Thorne, and John Wheeler. Dating from 1973, Gravitation is known as MTW and is a mighty 1,279 pages long. It’s considered to be the bible of general relativity. You can perhaps find a pdf online. On page 848 you can see figure 32.1, which shows free-fall Schwarzschild coordinates on the left:
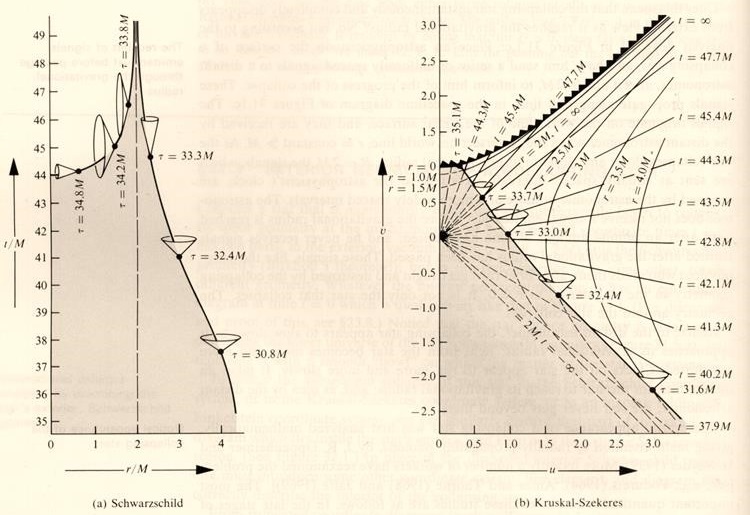Image by W H Freeman and company, publishers of Gravitation
The horizontal axis denotes distance, and the vertical axis denotes time. The vertical dashed line is at r = 2M and denotes the event horizon. The curve on the right denotes the path of an infalling body outside the event horizon. It gets closer and closer to the event horizon as the time t increases. Note though that the time axis is truncated, obscuring the way the infalling body somehow manages to cross the event horizon at time t = infinity. Then it comes back down the chart, tracing out the curve to the left of the vertical dashed line. It ends up in the central point singularity at r = 0 at proper time tau τ = 35.1 M. Yes, according to MTW an infalling body goes to the end of time and back. But that’s not all. If you look horizontally across the Schwarzschild chart at time t = 45, you will notice that the infalling body is at two locations at the same time t. It’s outside the event horizon with a proper time τ = 33.3 M, and at the same time it’s inside the event horizon with a proper time of circa τ = 34.3 M. That’s why you read about the elephant and the event horizon, where the elephant is in two places at once.
Eddington-Finkelstein and Kruskal-Szekeres coordinates
The issues go on. MTW also refers to Eddington-Finkelstein coordinates. See box 31.2 on page 828, which says Eddington and Finkelstein used free-falling photons as the foundation of their coordinate system. However the Wikipedia article says this: “they are named for Arthur Stanley Eddington and David Finkelstein, even though neither ever wrote down these coordinates or the metric in these coordinates. Roger Penrose seems to have been the first to write down the null form but credits it (wrongly) to the above paper by Finkelstein, and, in his Adams Prize essay later that year, to Eddington and Finkelstein”. The article also says “one advantage of this coordinate system is that it shows that the apparent singularity at the Schwarzschild radius is only a coordinate singularity and is not a true physical singularity”. Eddington-Finkelstein coordinates employ a “tortoise coordinate” which is like Zeno’s paradox in reverse. The time unit used in the coordinate system gets bigger and bigger as you approach the black hole. Hence it allegedly cancels out the gravitational time dilation, increasing to infinity at the event horizon. Kruskal-Szekeres coordinates are similar. Hence the chart on the right of MTW page 848 has done away with the troublesome trip to the end of time and back. It has done a hop skip and a jump over the end of time and swept the problem under the carpet. The conclusion is then that a star collapses to a singular point of infinite density in finite time:
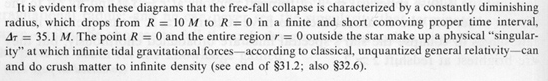Fair use excerpt from Misner Thorne Wheeler’s Gravitation
There’s just one little problem with that: light curves and an infalling body falls down because the speed of light is spatially variable. Your pencil falls down because the speed of light near the floor is lower than the speed of light near the ceiling, and there’s a gradient in between. But at the event horizon the speed of light is zero and it can’t go lower than that. So there is no more gravity. If we could somehow place our gedanken observer at the event horizon, he wouldn’t fall down. Nor would anything else. There is no gradient in gravitational potential, so there’s no further collapse, and no tidal forces. But the speed of light is zero so there’s no observing either. This is a crucial point.
Hawking did not understand gravity
Unfortunately many physicists are unaware of it. For example, one of Stephen Hawking’s “seminal” papers was singularities and the geometry of spacetime dating from 1966. On page 26 he referred to the Schwarzschild metric and the “apparent” singularity at r=2m. He said it was “simply due to a bad choice of coordinates”. On page 76 Hawking talked of “such a strong gravitational field that even the ‘outgoing’ light rays from it are dragged back”. It’s clear Hawking had never read Einstein’s fundamental ideas and methods of the theory of relativity. That’s where Einstein explained why light curves. It’s clear that Hawking did not understand that a gravitational field is a place where “the speed of light is spatially variable”. He didn’t know that in a gravitational field, “light speeds up as it ascends from floor to ceiling”. He didn’t know that in a strong gravitational field, outgoing light rays aren’t dragged back. They speed up even more. Hawking didn’t understand the first thing about gravity, so he didn’t understand the first thing about black holes either. If you think that’s bad, it gets worse. A lot worse.
He sees nothing
If we could lower a gedanken observer into a black hole such that we could watch him approach the event horizon through some gedanken camera, we’d see his optical clock going slower and slower until it stopped. We’d see him stop too. Kruskal-Szekeres coordinates try to cancel out the stopped clock with the stopped observer, who is somehow supposed to see the clock ticking normally “in his frame”. It is said that he sees nothing unusual. But Kruskal-Szekeres coordinates contain a schoolboy error, because at the event horizon the speed of light is zero. So the gedanken observer can’t see. His light is stopped, and because of the wave nature of matter, so is he. Electrochemical signals in his nerves and brain do not move. So instead of seeing nothing unusual, he sees nothing. Ever. Which means Kruskal-Szekeres coordinates are like some dead parrot sketch, where the shopkeeper swears that a dead customer sees the dead parrot squawking normally. Which means the singularity at r = rs is not just a coordinate singularity. You can’t get past it by inventing a fantasy coordinate system where seconds last forever. Gravitational time dilation goes infinite, so there are no more events, so there isn’t any time, so proper time isn’t proper at all. Yes, in general relativity we talk of coordinate independence and say all coordinate systems are equal. But when light has stopped we can’t measure seconds and metres, so that’s where all coordinate systems end. They are all equal, but there is no never-never land beyond the end of time.
What a black hole is
We now start to get a clearer picture of what a black hole is. The central point singularity has gone, and in its place we have a place where you can’t go. As such it’s akin to the gravastar, featuring a “gravitational vacuum”, a void in the fabric of space and time. This fabric is like some gin-clear ghostly elastic, which is why the stress-energy momentum tensor features a shear stress term. The black hole is a hole in this fabric, so the frozen-star black hole is more of a hole than the point-singularity black hole. In simulated images it even looks like a hole. Think of a blue-grey party balloon, somewhat translucent, with a starscape painted on it. Now add a bullethole whilst keeping the balloon intact. What you have is Alain Riazuelo’s black hole depiction:
CCASA simulated image of a stellar black hole by Alain Riazuelo see Wikipedia
But whilst it looks like a hole in space, the frozen-star black hole is like solid space too. Rock solid, because it’s a place where c is zero, so there can be no motion. And if there can be no motion there can be no angular momentum. There can be no spin. We can find articles that say a black hole spins at nearly the speed of light. But the speed of light at the event horizon is zero, so that creates a problem for the Kerr black hole. Since however Kerr black holes are associated with negative space and wormholes and other universes and time travel, I don’t think that’s a problem myself. In similar vein a charged particle has a Poynting-vector energy flow going around and around at the speed of light. But at the event horizon this speed is zero, so that creates a problem for the Reissner-Nordstrom black hole. Since however Reissner-Nordstrom black holes are associated with naked singularities and one-way wormholes that connect to white holes in another space and time, I don’t think that’s a problem myself. Particularly because of the mass inflation and the infinite blueshift. Conservation of energy rules this out. When you drop a 511kev photon into a black hole, you would say the black hole mass increases by 511keV/c². So the photon didn’t gain any E=hf energy or increase in frequency as it descended. You and your clock go slower when you’re lower, so you measure the selfsame frequency to be higher, that’s all. It’s similar for gravitational redshift. Einstein said this in 1917: “an atom absorbs or emits light at a frequency which is dependent on the potential of the gravitational field in which it is situated”. The frequency doesn’t reduce as the photon ascends, it was already lower when the photon was emitted. The ascending photon does not reduce in frequency. It does not lose energy. There is no magical mechanism by which a photon in space loses energy. There is no magic, there is no time travel, and despite what the Penrose diagrams say, there is no wormhole, or parallel universe, or parallel antiverse:
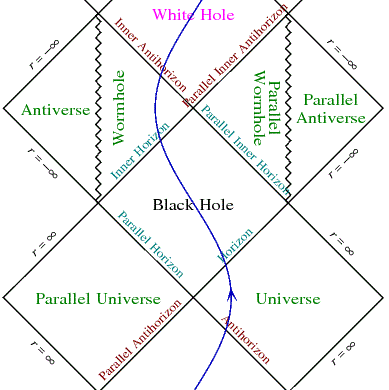Penrose diagram by Andrew Hamilton, cropped by me
Some would say that the frozen-star black hole cannot be correct because nothing passes through the event horizon, and therefore black holes cannot grow. After all, that’s more or less what Einstein said. But think in terms of a hailstone. A hailstone doesn’t grow because water molecules pass through its surface.
Black holes grow like hailstones
Imagine you’re a water molecule. You alight upon the surface of the hailstone. You can’t pass through this surface. But you are presently surrounded by other water molecules, and eventually buried by them. So whilst you can’t pass through the surface, the surface can pass through you. So the frozen-star black hole grows like a hailstone. The event horizon expands outwards from the centre of a collapsing star. Which consists of matter, falling down because of the wave nature of matter and because light curves where the speed of light varies. You can think of an electron as light going around and around, then you can simplify it to light going round a square path, then you can imagine it’s in a gravitational field. The vertical parts of the path stay vertical, but the horizontal parts bend down a little, so the electron falls down. The reducing speed of light is transformed into the downward motion of the electron. It’s all rather simple and straightforward when you know how gravity works. There are no messenger particle. There is no magical mysterious action at a distance. There is no mystery to it. The mystery is how a black hole falls down, and how LIGO could have detected a black hole merger. There’s another mystery too. Something that grew out of gamma ray bursts, which we’ll come back to another day. Something that used to be called the Hawking effect. It’s nowadays called Hawking radiation.
Nice idea to describe a black hole as a hailstone, building up layer by layer. (I rather imagine a pavement covered by old chewing gums:-) When asking about the event horizon on PSE it is interesing to see how everyone goes a great length to confirm that the observer sees nothing special. Who bloody cares. If I look at my kitchen clock, my question is: did the observer reach the event horizon by now, will he tomorrow, will he in a gazillion years? And according to what I understand from the formulas, the answer is plain NO! Now if that observer does not reach the event horizon any time soon, how then is the matter going to collapse into a singularity any time soon?
As you describe, the progression of time is not so much different from the progression of light. Measuring the speed of light by how long a beam of light takes to travel a meter using a clock that defines time by how long light takes to travel a meter, of course local measures of $c$ are always the same. Again, who cares. According to my kitchen clock, neither light nor time can progress near the even horizon, so neither matter nor energy will progress; how should it collapse.
What I wonder is, how the space behind the event horizon can be described when its like frozen. There are nice thought experiments here https://physics.stackexchange.com/q/304776/73067 and here https://physics.stackexchange.com/q/421036/73067 but the answers are depressingly similar in trying to explain that this is a short lived situation and much too complicated to describe today 🙁
Maybe this singularity-business is much easier than commonly thought. In a certain way, space is like the trunk of your car: when its full, its full. There is no singularity in the middle of your luggage:-)
Good stuff Harald. I so dislike point singularities. I also dislike a lot of what I read about black holes. The first stack exchange question misses the trick that there is no mechanism by which a black hole falls down. Light curves downward because it’s moving through inhomogeneous space. The electron falls down because it’s a “dynamical spinor” which again features motion through inhomogeneous space. So what happens when there is no motion, because the gravitational time dilation has gone infinite? The stack exchange question asks if there’s reason to think any of the laws of physics would be different in this region of space? I’d say when there is no motion, there are no laws of physics. The second stack exchange question misses the point that a gravitational field is a place where the speed of light is spatially variable, and light can’t go slower than stopped. And yes, the answers are not good. In fact they’re useless. And on stack exchange, the people who give those useless answers conspire to delete good answers. Like my answer here. If you can’t see it please let me know and I’ll send it to you. As for what this “frozen space” is like I can’t really say. Perhaps it’s something like a BEC. I do find the Bosenova interesting. But there again, perhaps it’s not.
Hi John,
indeed I cannot see the answer you link to.
As for the general problem of the singularities and the speed of light inside the event horizon, I wonder what your take is. In https://physics.stackexchange.com/questions/421036/overlapping-gravitational-field-of-non-black-holes-formally-creating-a-black-hol I try to conjure up a situation where the gravitational potential is larger even than on the event horizon. If time and the speed of light depend on the gravitational potential $-GM/r$ according to (for local time increase with regard to observer time) $\frac{dt}{dt_0} = \sqrt{1 – \frac{2GM}{c_0^2 r}}$ then what does it mean that the potential gets even greater. As you say often, slower than $0$ is not an option. Would you assume that the potential in the overlapping area, or inside the event horizon does actually not get greater than $-GM/r_s$, for example because the reach of gravitation is slowed down to zero at the event horizon too?
I think the situation would be much the same as if you were between two stars. At the midpoint the gravitational potential is low and the gravitational time dilation is high. There’s no gradient in gravitational potential and so no force of gravity. But if you stepped one side there would be. I can plot the potential like this:
Harald, here’s my answer:
.
Does the equivalence principle give us a means to tell if variations in the coordinate speed of light have absolute or only relative significance?
.
No. Scientific evidence tells us that black holes exist, and therefore the coordinate speed of light has an absolute significance. So much so that you can drop the word coordinate.
.
In general relativity the local speed of light is a constant and has the usual value c, but the speed of light that we measure from here for a part of space over there (called the coordinate speed) may differ from the accepted value.
.
Correct. But the reason why we always measure the local speed of to be 299,792,458 m/s is because of the wave nature of matter, and because we use the local motion of light to define our metres and our seconds. It’s a tautology. See https://arxiv.org/abs/0705.4507.
.
This is one way to structure arguments about gravitational red/blue shift
.
The ascending photon does not change frequency. It is emitted at a lower frequency. Because things go slower when they’re lower. See page 149 of Relativity, the Special and General Theory. That’s where Einstein said this: “an atom absorbs or emits light at a frequency which is dependent on the potential of the gravitational field in which it is situated”.
.
and the curvature of light paths relative coordinate systems fixed to a particular observer. It is a common way of explaining the Shapiro delay.
.
See the Wikipedia Shapiro delay article: “according to the general theory, the speed of a light wave depends on the strength of the gravitational potential along its path”. Light curves because the speed of light varies in line with gravitational potential.
.
Indeed in that kind of context this point of view is successful enough that it is tempting to take it as definitive. To say “the speed of light really does vary from place to place
.
It’s what Einstein said.
.
the constancy of the local speed is an artifact of using the motion of light to define our measure of time.
.
Yes. Once you “see” the tautology it’s scarey just how simple and straightforward it is, but people just don’t get it.
.
How does the equivalence principle come into play?
.
It doesn’t. The principle of equivalence applies to an infinitesimal region only, To a region of zero extent. So it doesn’t apply at all. This is why Einstein said special relativity is nowhere precisely realized in the real world. It’s also why John Synge said the midwife should be buried, see page ix and x of relativity: the general theory.
.
Not being a relativist in any serious way myself (my sole course on general relativity is more than twenty years in the past!) I’ve been wondering about how that notion gets along with the equivalence principle.
.
The equivalence principle is a mess. See the mathspages article on the many principles of equivalence where you can read that the equivalence principle has undergone several changes over the years. Brown says “the modern statement of the strong equivalence principle, of the assertion that the laws of physics are the same for all frames of reference (i.e., independent of velocity) is also conceptually quite distinct from the original meaning of Einstein’s equivalence principle”. John Norton reiterates this in his 1985 paper what was Einstein’s principle of equivalence? He said it was a special relativity principle that dealt only with fields that could be transformed away. He talked of an old view and a new view, and said “the equivalence of all frames embodied in this new view goes well beyond the result that Einstein himself claimed in 1916”.
.
I try to isolate the question with the following thought experiment. Two (identical) space craft are commanded from their geometric centers and also feature a pair of transverse light clocks a height L/2 “above” and “below” the cockpit. While accelerating the “high” clock should accumulate more time than the “low” clock just as they would if the ship was grounded upright on Earth.
.
It won’t.
.
Now we imaging these two craft hurtling toward each other in deep space while they both employ a steady thrust to reduce their closing velocity in such a way that they arrive at relative rest just as their cockpits come alongside one other. At this instant, the two occupants of the two craft momentarily share a single co-moving frame of reference. Naive “paradox” However, occupants of each craft will report a different expectation for the relative timing of the clocks. In particular occupants of craft A see clocks A high and B low as above them and therefore running fast while clocks A low and B high are below them and therefore running slow. Occupants of craft B of course have the opposite expectations.
.
There are no paradoxes.
.
Of course the occupants of both crafts are in non-inertial frames, an observer floating freely nearby will report that both ships exist in a flat space-time for which the coordinate speed of light is everywhere equal to the local speed of light.
.
In this context a reference frame is little more than a state of motion.
.
What’s the point In my naive view this scenario demolishes claims that the coordinate speed has some absolute significance because * It arranges a paradox if we believe in absolute significance of the coordinate speed. * Viewing differences in the coordinate speed of light as having only relative consequence would seem to have no problem with the described scenario. Is this a sustainable conclusion or is there something that I am missing (that is: is there a correction I’m failing to make that prevent the “paradox” from coming up in the first place thereby leaving the ontological question unresolved)?
.
Yes. The equivalence is not exact. Accelerating through homogeneous space is like being stationary in inhomogeneous space, but it is not the same. You can distinguish between being in the accelerating spaceship and being in the spaceship sitting on the surface of the the Earth by comparing the upper clock with the lower clock. If they differ, you’re on Earth.
.
Neither of Gravity, Acceleration, Time Dilation and the Equivalence Principle Time dilation in a gravitational field and the equivalence principle address the question of what significance should be understood for variations in the coordinate speed of light.
.
You are missing the significance of the “absolute” view. I know it runs counter to what people say about general relativity, but you can gauge your motion through the universe by looking at the CMBR. It’s not some absolute frame in the traditional sense, but that motion is as absolute as it gets. In addition, black holes are black because the light can’t get out. Because the coordinate speed of light at the event horizon is zero, hence the upward-pointed light beam doesn’t ascend. This applies for everybody. Even for the gedanken observer at the event horizon with his optical clock. Gravitational time dilation goes infinite. His clock is stopped, and he’s stopped too. Contrary to what Kruskal-Szekeres coordinates suggest, the stopped observer doesn’t see his stopped clock ticking normally “in his frame”. He sees nothing. Ever.
.
This answer has a net 6 downvotes and was “Deleted by AccidentalFourierTransform, Kyle Kanos, knzhou May 31 at 15:50”.
John,
the point I am trying to make is that time dilation and the speed of light measured in coordinates of the observer at infinity seem pretty much to depend on the the gravitational potential. At the event horizon, we reach the point where the potential is high enough for infinite time dilation and zero speed of light. Inside the event horizon, time dilation cannot be higher and the speed of light cannot be lower, so there are statements like “time and space change roles”, time runs backwards and what not. While this may formally, mathematically be true somehow, I wonder if there could be a better explanation which simply says: the potential cannot get higher than on the event horizon, at least not in finite coordinate time, because the gravitation “cannot get in in finite time in the same way as light come to a halt at the event horzion” (however this may be formulated in term of gravitational waves, maybe)?
I agree with all that Harald. Light can’t go slower than stopped. Time dilation can’t go greater than infinite. That’s the inevitable result you reach once you know that a gravitational field is a place where the speed of light is spatially variable. It means most of what we’ve been told about black holes is wrong. All that stuff about point-singularities is wrong. As is all that stuff about “time and space change roles”. There is no basis for that. Motion stops at the event horizon, and that’s that. Everything else that is said to happen only happens in some never-never land beyond the end of time. Which means it doesn’t happen at all. It also means Hawking radiation doesn’t happen either.
Hi, I am glad having found this blog and some ideas quite similar to mine.
“An optical clock at the event horizon doesn’t tick at all, like Einstein said. And when you understand the nature of time, you know why. It isn’t because some abstract thing called time stops. It’s because light stops. Because the speed of light at the event horizon is zero. That’s why the light doesn’t get out of the black hole. Not because of some mystic curvature that makes vertical light beams bend back round. Not because the sky is falling in. But because at that location, the speed of light is zero. The light isn’t moving, so it doesn’t go up. It doesn’t get out because it is effectively “frozen”. That’s why a black hole is black. Because it’s a frozen star.”
I agree that mostly, but I wouldn’t say it quite this way. I think, the main reason really is that time stops at even horizon. Matter is frozen, and hence there is no such events to launch photons. Events are requiring normally ticking time.
A light ray has always infinite time dilation but still it is moving from normal observer’s point of view. From light’s point of view it doesn’t need any time to move, it proceeds in a zero time even from the release moment of CBR to the ultimate end of universe, if not colliding to anything. How could something that is not consuming any time accelerate? Normal gedanken observers are recognizing the speed of light as constant, everyone with his own subjective time. Therefore I wouldn’t quite say that light speeds up, because no one particular observer is measuring the change of speed caused by change of gravity.
Event horizon’s infinite time dilatation doesn’t stop gravity waves generating. They might be generated by nearby time space’s anomalies, therefore not necessary originating from inside of merging event horizons.
I have been wondering why the quantum mechanics of black hole is treated on completely different and quite speculatively basis as events in big bang’s commonly accepted early quantum mechanics. It would feel natural that contrariwise events would happen when mass is pressed towards zero volume. The most important question is if the inflatory field or force would be activating, maybe preventing collapsing mass to be pressed into a point singularity, producing thus some kind of ‘fuzzy ball’ instead, which could match to the timeless situation inside event horizon.
I’m awfully sorry Jorma, your comment was in my spam folder, and I didn’t check it. Utmost apologies.
.
The important point about time is that there is no fundamental thing called time. So optical clocks go slower when they’re lower because light goes slower when it’s lower. See https://physicsdetective.com/the-nature-of-time/ and https://physicsdetective.com/the-speed-of-light/ for details. Normal gedanken observers think the speed of light is constant because they use the local motion of light to calibrate their meters and seconds, and them use them to measure the local motion of light. You might not say light speeds up, but Einstein did, time and time again.
.
I don’t have an issue with gravitational waves, because waves are more fundamental than fields. But I do have an issue with the merging black holes spiralling towards one another, as if they’re ordinary matter.
.
See the subsequent articles for information about the quantum mechanics of black holes. I’m afraid some of it is very speculative indeed. I’ll be writing about inflation soon. And the early universe, where the timeless situation seems to be similar to that inside a black hole.
So then why do “black holes” create realtivistic jets?
Because they “burn” matter and convert it into gamma radiation, which blasts other matter out. The black hole functions as a kind of jet engine. I’ll be posting my next article on Saturday which says more about this.
Excellent blog, thank you for all the articles John, golden info really! Mind opening stuff. One question, now that we saw yesterday(10/4/19) the first image of the M87 black hole from the EHT project and all the info about it pointing to it being actually a spinning kerr black hole , what would you comment now ? You said above that zero speed of light at the event horizon causes a problem for the existance of spinning kerr black holes, if I did understand what you said correctly. Thanks!
Hi Akis, thanks re the golden info. The reports I read talked about the accretion disk, and quoted one of the scientists saying they didn’t know what lay within the event horizon. Can you refer me to the report you read which talked about a Kerr black hole?
Hi John,
I read the paper they put out yesterday and saw all the vids/presentations from the EHT team as well as the answers on reddit (to the Q of the public by many participating scientists in this project)..fascinating info! So much relative info is out there now..(we live in exciting times my friend!). Here is a quote from forbes website (but same info is to be found in the released papers etc) : https://www.forbes.com/sites/startswithabang/2019/04/11/10-deep-lessons-from-our-first-image-of-a-black-holes-event-horizon/#78ef380755e6
“3. This has to be a rotating black hole, and its rotation axis happens to point away from Earth. With observations of the event horizon, the radio emissions surrounding it, the large-scale jet, and the extended radio emissions that were measured previously by other observatories, the Event Horizon Telescope Collaboration has determined that this must be a Kerr (rotating) and not a Schwarzschild (non-rotating) black hole.”
—–
Also from Astronomy.com:
https://astronomy.com/news/2019/04/the-nature-of-m87-a-look-at-a-supermassive-black-hole
Overall,” the paper states, “the observed image is consistent with expectations for the shadow of a spinning Kerr black hole as predicted by general relativity.”
so for further details I suggest you have a look to the scientists released info/paper etc. The existance of Kerr rotating black holes is not consitent with what you say about the BH being frozen stars etc so I would love to hear what you make of all the new info. Thank you for all the shared info and explanations on all different kind of topics again! Looking forward to your reply!
Cheers
Akis
Thanks Akis. The first one is by Ethan Siegel. He and I sometimes have discussions about his posts on Patreon. I sometimes object to him promoting unproven speculations. Of course, he’s not alone in this. Some experimentalist comes up with some fairly ordinary observations, and some theorist jumps up and claims that it’s rock solid evidence for M-theory or the holographic universe or the multiverse or something.
.
However your second reference says what it says: “the observed image is consistent with expectations for the shadow of a spinning Kerr black hole as predicted by general relativity”. It also says “it still managed to uncover evidence that M87’s supermassive black hole rotates in the same direction as its accretion disk”. However when I read the paper I can’t see any solid support for this. They say “models in our library of non-spinning black holes are inconsistent with the observations as they do not produce sufficiently powerful jets”. But they also say this: “There is no consensus model for jet launching”. I’d say the observations are consistent with models developed by people who don’t understand why gamma ray bursts occur. Note this “Here ${a}_{* }\equiv {Jc}/{{GM}}^{2}$, where J, G, and c are, respectively, the black hole angular momentum, gravitational constant, and speed of light. They don’t even know that the speed of light varies in a gravitational field.
.
See section 7.4 where they don’t rule out alternatives. Funnily enough they use the phrase “many exotic alternatives to Kerr black holes”. Perhaps they don’t appreciate just how exotic the Kerr black hole is. I’ll dig further. But meanwhile, something I’m a little suspicious of here is that we have a big collaboration with teasers and hype, and they’re drawing an awful lot of conclusions from some rather hazy observations.
Well the reason I decided to post in your blog is you opened my eyes regarding the variable speed of light, what gravity is and how it works, why objects/matter falls down, what a photon is etc etc…My mind was blown and I could connect all the missing dots and finally understand physics at a whole new level! Your writings made so much sense. I fell in love with Physics again! So many unanswered questions and so many unconnected things suddently all made sense and could now be unified in my mind! You are the best physics teacher I ‘ve had! 😉 no BS and all of them had studied Physics 😉 I thank you for that. My ex is a theoretical physicist (cosmologist / astrophysicist) and I love physics too especially Optics, so I always talked with her about such topics..I was usually skeptical about the mainstream explanations and theories…as wrong info and misinformation is to be found in all sciences and topics..I even questioned her about the speed of light once and told her that from my understanding it has to be variable, and that is seems more plausible to my eyes than it being constant..then I did some research to show her proof searching if there was any supporting info on that and had found the wiki article on VSL, that was back in 2016…and saw only very few scientists that supported this theory..
So it seemed like a ..not very accepted idea..and stupidily I moved on without looking back..
At that point as a visual guy I was trying to understand how the universe and space /curved spacetime really works at a practical level with tanglible evidence to support those explanations..and understand reality.
Unfortunatelly I did not go very far..but as a computer graphics artist I had manage to make the blueprints for a universe simmulation/visualization model where in 3d virtual space ( in the computer ), the space (representing the space in our universe) with areas with curved spacetime, they were being represented with the following proeprty, the objects in there had a size that varied, ie the higher the space energy density in that aera the more the reduction in object size (now I think of it..I was effectivelly simulating the slower VSL speed of light as the smaller object will have smaller relative speed and thus moving more slowly in this (‘denser’) space – curved spacetime / it would take the small object a longer time to move accross a meter of more bent space compared to a meter of unbent space)..
Then last year I did some research again alone this time on the VSL topic again and ta-da I found your blog! I was in heaven lol… Really deep understanding you have my friend. Your way of thinking is very solid and logic / evidence based and I like that you helped me to go read einstein’s own paper’s saying’s and work on VSL and other topics. Something most physisists don’t even bother to do yet comment as if they have… I was blown away! Yep VSL was indeed the real case according to Einstein himself..
So if I understand things correctly space does seem to be like glass-ether like, refracting light, the more the energy density the more the bending of the light..the more the gravitational potential..and the higher the space energy density the less the matter can ‘change'(‘move’) over time/ the less easy matter can overcome time in a way so to speak. Its as if curved spacetime is simply the more dense area of the clear gin gel you like to compare it to..
The higher the energy density there , the less freedom is left for ‘things’ to do ‘stuff’ lol
I would compare it with a busy highway road, not allowing others to move feely (/ do work) inside in these fully filled lanes.If the traffic gets too much after a critical/saturation point all the movement stops..
Same with speed of light and space energy density, bholes are the areas where too much mass/energy compacted in a small space that nothing can escape/move there..
But maybe its not that simple..? I dunno I am still confused about some stuff myself..
Yes black holes should be frozen stars as fas as I understand too, due to infinate time dilation at the event horizon etc speed of light reaching zero. Like yourself I am a big skeptic too (and certainly a consipracy theorist) so I do not automatically accept what we are being told by ‘authorities’ or people in white lab coats just cause I am told so..I was surpirsed by what you said about Gravitational waves and the 2 black hole merger gravitational waves..but it makes sense!..how can black holes move around each other in space etc if the speed of light at their event horizons is infinitelly slow/reaching zero (meaning no movement whatsoever)! Same case with the Kerr rotating black hole now..Thats why i wanted your input..as what we are being told now is that this few pixels wide blurry image / visualization..is actually proof of a spinning black hole..as its matches their theoretic modeled sims..
If its not a spinning Kerr BH , what do you think these jets are and show , just a rotating accretion disk ?
I’m honoured, Akis, and flattered, Thank you. That I fell in love with physics again makes it all worthwhile. Shame about your ex. I don’t suppose you could use any of this stuff to your advantage? See my strapline about looking at past papers. There’s some great stuff by some great authors, and not just Einstein. Once you’ve read those old papers then IMHO it’s astonishing that they’re not common knowledge. And once you know that a gravitational field is a place where space is inhomogeneous, then you ask yourself where is it curved? That’s a whole new world of adventure.
.
Yes, it is that simple. You might be confused now, but as you read more you won’t be. Especially when you find that it isn’t just me saying this stuff, it’s Einstein and other famous physicists. Then you’ll form a different view about the people in white lab coats. But don’t blame them all. It’s a funny old business is physics. And cosmology of course. There are reliable solid people doing great work, and there are the hucksters too. Anyway, I think a black hole is a bit like a plughole, and a bit like a jet engine too. Infalling matter goes round and round in an accretion disk, but at some point it disintegrates into photons and neutrinos. Basically it turns into gamma-ray burst energy that blasts out other matter. A jet engine does something similar, but the jet is orthogonal to the rotation, and is constrained at the sides. I imagine a black hole could blow away its accretion disk, but I also imagine that would be a rare event. Most of the time the accretion disk would function as the walls of the jet engine.
.
I also think all the rotation is outside the event horizon. And that angular momentum is conserved too, because the gamma ray burst occurred.
Ok so that I get this straight, can you please explain to me how you you understand things are near the event horizon? If the gravitational ‘pull-in’ force of any heavy object (ie BH) accelerates a person’s speed when he is approaching it, and he falls infaster and faster..why when we reach the event horizon all matter/energy, even light reaches zero speed/stops moving?
Is it because gravity pulls us in towards something heavy, faster and faster ..but only up to certain point? …then the increasing ‘resistance’ from the higher ‘energy density’ of the space near the heavy object starts to take over (as opposite direction force) and starts slowing us down instead..till we reach so close that we reach the EH where even light speed is reaching zero?
Till at the EH, the light ‘hits a wall’ of high energy density..so ‘thick’ that nothing can move in it..do I get this right?
What I try to warp my head around is, if an object approaching a bh, its pulled in faster and faster by the great, concentrated, mass of the bh, ..when does this accelleration stop and the decceleration start though? At which r / point do we have zero acceleration that is? (probably will depend on the object and bh masses).
Is this the reason why the scientist of the EHT say that its hard if not impossible for us to shoot an object straight into a black hole, and that it would end up in orbit instead (and not fall in)?
Cheers
You need to read my firewall article, Akis. Rather counterintuitively, the descending light beam slows down. But falling bodies don’t. If you fall into a black hole, you fall faster and faster because the speed of light is getting slower and slower. If this continued without limit, you’d end up falling faster than the local speed of light. That surely can’t happen, because of the wave nature of matter. And as you know falling bodies do not slow down. So something else surely has to happen. I think a gamma ray burst happens. Friedwardt Winterberg worked that out in 2001. He’s the guy who had the idea for GPS.
It seems to me that in your theory of physics, since the speed of light is spacially variable and gravity is caused by concentrations of curved space causing this C variability, it follows that there is some kind of absolute refernce frame related to space away from any gravity fields (even if said frame is unknowable to us stuck in our refernce frame) because space must be some kind of substance. if so, and if a black hole is an area where the speed of light is zero and therefore all motion (and motion’s emergent property, time) stops, then mustnt that black hole then be standing still relative to this absolute refernce frame? How can it still , say, orbit a galactic center? If a thing feel gravity because its particles are photons moving around in circles and the horizontal components of those circular paths bend down in a gravitational field, how can a black hole respond to another body’s field if the internal motions of its particles is zero?
That’s a good comment, Gary. Note though that the spatially variable speed of light is Einstein’s theory of physics, not mine.
.
I don’t think there’s any absolute reference frame in the general relativity sense. Yes, the CMBR gives us a “universal” reference frame, and the universe is as absolute as it gets. But there’s no way you can tell you’re moving if you’re inside some windowless box that’s at rest or in uniform motion with respect to the CMBR. So I’m happy that a black hole keeps on moving once it’s formed.
.
But I don’t know how a black hole falls down. As far as I can tell, there is no mechanism whatsoever for a black hole to be affected by gravity. Hence I just don’t know how two black holes can circle one another.
I know it’s Einstein’s theory, and I think it’s right. Of course to any observers made of matter (space waves) every frame seems equivalent, since we are bound by our local C which dictates how we measure time and space. But regardless of “observers” (why should the universe care if there are observers?) there must be some universal absolute frame if space is some kind of “ghostly gin-clear elastic” (even if one can never tell if he is in that frame) so if a black hole is an area of “frozen space waves”, frozen relative to what? Must be that absolute frame? But there is good evidence of black holes in our universe and they are certainly moving relative to eAch other so if those are indeed black holes that can’t be right. Maybe a BH is frozen relative to its own frame it had since before it contracted down to event horizon, , so in a frame that’s moving relative to the BH it’s not seen as quite a black hole, (or seen as anything haha) until it’s gravity pulls you into it and you now share its frame.
Also, the gravitational field outside the event horizon, where c is above zero, can hence still move through space, maybe it drags the frozen star inside it with it?
An analogy I’m thinking of would be to imagine space as a material, which has a possible lowest density state (the universal absolute reference frame) and the speed of sound (waves) in this material is C. There are areas where sound waves and standing sound waves in the form of spinors are concentrated, which decreases the local speed of sound, in a decreasing gradient as you get closer to center of energy density) In these areas observers made out of standing sound waves still measure the speed of sound as c since their measure of time is dictated by their local speed of sound; and spinors fall down because their horizontal component bends down because of the gradient. The question is, if a region where the density of this material is so high due to a concentration of sound waves and/or sound spinors that the speed of sound through this region is zero exists, do they even exist as waves anymore, and can this region continue to move through the material?
Can a black hole be accelerated?
Sorry to be slow replying Gary. If a black hole is an area of “frozen space waves”, they’re frozen relative to other waves in local space. It’s like you walk into a crowd, and it’s so crowded you can’t walk any more. But you could be in a crowd on the deck of an aircraft carrier moving relative to some other crowd on the deck of some other aircraft carrier. That’s how I see it anyway. Frozen relative to its own frame before it became a black hole sounds right. If you’re moving relative to it you’d still see it as a black hole. It’s black. Light can’t get out. Your relative motion doesn’t change that.
.
Maybe the gravitational field outside the event horizon has some effect on the black hole. The trouble is I don’t know how.
.
Your sound analogy sounds right. But observers in a place where the speed of sound is zero don’t measure anything, ever. Do they even exist as sound waves any more? I think not. What you’ve got is some big amorphous region where the speed of sound is zero, Like all the sound waves merged into one. I am reminded of a Bose-Einstein condensate.
.
Can a black hole be accelerated? I don’t know how it can be. If a star was heading towards the Earth, and if it turned into a black hole, the black hole would go straight through the Earth and would just keep on going. Google on wandering black hole.
I think black holes could be accelerated in your model. Einstein said, in effect, that light never actually reaches the event horizon. So there is a lot of energy still zipping around while it falls in, albeit at ever more slow speeds. So there may be enough to accelerate black holes towards each other. It’s a question of the growth of the hailstone verses the dynamics of the potential.
So what LIGO could be measuring is a shock wave in space due to the shock in the event horizons.
I don’t know Alan. The black hole is black because light can’t get out, because the speed of light is zero. So there are no dynamics. So I don’t know what LIGO are measuring. Perhaps it’s a passing truck. Perhaps they haven’t measured anything at all. When a church needs a miracle, a church gets a miracle.
The way I see it is that black holes are things that can move in space like everything else. And they are affected by gravity like everything else, and generate gravitational potential. So they can attract each other.
.
They have mass, lots of it. Which is energy. They don’t contain any matter though – nothing happens on the inside, there are no waves, no motion, no time, no dimensions, no nothing. They are dead. Or undead, because there has to be energy which is something, and it’s fundamental. Can I say zombar (zombie star)? So I think of it as a region of space with nothing but bound energy – frozen because it’s maximally dense. (A region, not a singularity, because those are not real.)
.
Nothing can enter (except another black hole); all infalling matter is radiated away or smeared on the surface.
.
They can spin though, no problem there. And outside, their gravitational pull wreaks havoc on space and there is massive magnetism and frame-dragging and accretion and jets of radiation. Galaxies revolve around them.
.
So the event horizon is an impenetrable barrier. The point is that regardless of whether a black hole spins or not, its inside is fixed, has infinite entropy. It’s energy without space. It’s where “space is full”.
I share your sentiments on most of that. The big issue for me is how does a black hole fall down? I feel confident that I know how gravity works. I’m pretty sure that an electron falls down because electron spin is akin to light going round and round, at the speed of light,. The horizontal component of this is refracted downwards because the electron is an extended entity in a region where there’s a vertical gradient in the speed of light. But if the spin was frozen because the speed of light is zero, the mechanism by which the electron falls down just isn’t there. Scale this up to a brick, and then to a black hole, and I hope you see the problem.
You’re right, that mechanism cannot be there. But light tied up into matter is one thing; black holes are a special breed, they are not matter but pure energy. (I would even speculate that space and energy are somehow the two fundamental aspects of nature, with waves mediating between the two, and a black hole being one extreme where the duality ends, but I digress.) Galaxies do have peculiar motion though, Andromeda moving closer to us was the first thing Slipher saw in his blueshift measurement. That attraction is stronger than the expansion of the universe. And LIGO did measure something and it was surely a binary BH merger. So I don’t doubt that BHs attract each other. They have to – they are both massive so they have gravitational fields and they affect everything. If gravity isn’t involved all I can think of is opposite angular momentum. The frame-dragging of space may contribute too.
Yes, that mechanism cannot be there. I think space and energy are, in the end, the same thing. Yes, galaxies do have peculiar motion, and that attraction is stronger than the expansion of the universe. But as for what LIGO measured, I do doubt that black holes attract each other. Yes, they’re both massive, and they both have gravitational fields, but that mechanism by which matter falls down just isn’t there. Just as space doesn’t fall down, nor does frozen space. Nor does a black hole. What did LIGO detect? Maybe it was just a truck. Maybe it was nothing.
I hear you. But if two galaxies attract, such as the Andromeda galaxy and our Milky Way, and eventua;ly merge in a few billion years, what causes that? Would it not be the dance of the supermassive black holes in their centres that make that happen? After all, the billions of stars in their wake only follow their lead.
They’re just heading towards one another. Yes, the stars follow their lead, but do other black holes? I’d be interested to see some observations of galaxies with supermassive black holes orbiting other galaxies.
A link you posted in the “misconceptions in gravitational phyics” article states that there is indeed a universal reference frame, the ether (or simply space itself), and our movement through it is detectable via the doppler shift in the CMBR as a proxy. http://www.aether-theory.co.uk/totalsmallbook.pdf
That’s right Gary. Google on CMB reference frame. Also see Wikipedia. You can use the CMB to gauge your motion through the universe.
Enjoyed your blog post and generally agree with much of it. I spent about ten years researching fundamentals of gravity and have several papers. There are two things you might want to consider:
1. Whichever model of black holes one uses, it is hard to intuitively grasp that a black hole is mobile in space. It may either translate or rotate. The “freezing” of in-falling light is only with respect to motion relative to the black hole. The frozen photon and the BH may together be dragged about with no more inertia than their combined mass-energy. Just a point of curiosity. Not a contradiction of anything you said, provided the reference frame relativity is understood.
2. I spent a few minutes analyzing your spaceship paradox, as these are some of my favorite puzzles. You didn’t give a detailed development with calculations so I have to assume a bit about what you intend. And I don’t see how to upload figures in a comment, so bear with my abstract description. For others reading this post, allow me to clarify that a useful heuristic for quickly thinking about moving clocks is Leading Clocks Lag, see http://mc1soft.com/papers/2014-LeadingClocksLag.pdf . Another fundamental point which might be useful to readers is that ordinary clocks do not automatically re-synchronize themselves after acceleration, and aren’t fundamentally affected by acceleration. See Swann 1960 https://aapt.scitation.org/doi/10.1119/1.1934976 . Unfortunately no free copy is available.
In no case does the Principle of Equivalence claim the same physical processes are in effect in ordinary acceleration vis a vis a gravitational field. I mention this in case you are not aware. Many people assume otherwise. Einstein wrote a long paper prior to GR in which he gave an analysis of clock rates in an accelerating space ship using Doppler. In your example, the captain would see clock A running faster not because it is running faster – it is in fact unaffected by acceleration – but because he is viewing photons some time after they were emitted, and he is now moving faster than when they were emitted, thus they are blue shifted. Likewise the B clock is blue shifted. Were he to merely stop accelerating, the clocks would not be properly synchronized (per Swann) and he would have to adjust them using round trip light signals. Were he to decelerate back to his original frame, the Doppler shifts would unwind in the other direction exactly.
Now consider two space ships, with clocks A,B and A2,B2, headed toward each other at some high velocity. Assume each pair of clocks is duly synchronized in its original reference frame. They will not be after acceleration. We will leave them alone for the two captains to observe.
Initially the first captain observes his own clocks A and B in sync. The two clocks moving rapidly toward him appear skewed such that A2 reads an earlier time than B2 (Leading Clocks Lag).
The second captain observes his own clocks A2 and B2 in sync. The two clocks moving rapidly toward him appear skewed such that A reads an earlier time than B (Leading Clocks Lag).
These measurements are quite hypothetical, I hasten to add. And impractical. They only appear if the Einstein 2 on 1 clock measurement method is used (explained in the paper on Leading Clocks Lag). The space ships would have to be so long (or have long booms containing measurement apparatus) that they overlapped in the beginning in order to make this measurement. While theoretically possible, either the lengths of the ships or the amounts of deceleration are impractical.
Now as you proposed, the ships decelerate until they are adjacent and stopped and remain that way. In this post I will give only a qualitative description to save time. If you don’t believe something, we can work out the details. Both the amount of time skew and the perceived rate of increase or decrease in clock speed depend on γ, a, d and L/2, where d is the initial distance separating the ships and γ the initial Lorentz factor and the rest of it you have defined. These are not all independent. If d is larger, a will be less but will persist for a longer time, and so forth.
From the point of view of the second captain, A<B and they remain so, unaffected by acceleration. At the end he reports A<B. What does the first captain report of his own clocks?
His view is that they are initially in sync, but as he is decelerating A will run slower. At the end he will declare: "By golly, you are right, I now see A<B for my own clocks!"
And likewise for clocks A2 and B2, and so the two captains come to agreement on the final observation in which they are in the same reference frame, and there is no violation of the Equivalence Principle.
There are many aspects of General Relativity with which I disagree, at least as to interpretations, and generally I agree with your analysis of the Schwarzschild Radius. But the EP seems to hold up. I believe the reason is the same as the reason that time dilation is similar between General and Special Relativity. It is based on energy conservation. It takes a certain amount of energy to go from one inertial frame to another, always a positive amount. So the appearance of time dilation is symmetric. But in the gravitational field, it takes a positive amount of energy to go up and energy can be extracted from something going down, so the appearance of time dilation is asymmetric, and thus consistent rather than contradictory as in SR.
The point you make about coordinates, about some of them being unrealistic, I would take much further. Only in homogeneous coordinates does Noether's theorem naturally hold. These need not necessarily be flat but that is the simplest case. The entire universe could have a small constant curvature, but measurements in the late 1990s pin the possible value at very small levels. In homogeneous temporal coordinates conservation of energy holds, and in homogeneous spatial coordinates conservation of momentum holds. One can crank through and find that conservation of momentum results in a length contraction which is exactly proportional to the time dilation. Since length cannot be directly broadcast as time is, this is ambiguous. Length contraction is not experimentally distinguishable from spatial expansion (as long as one cannot produce a traversible wormhole, which doesn't seem likely). For mathematical development of exact GR (and some plausible alternative metrics) in this framework, see https://link.springer.com/article/10.1140/epjp/i2018-11983-2
Thanks Robert. I have no issue with the translational motion. But I start frowning when I hear about a black hole rotating at half the speed of light when a black hole is a place where the coordinate speed of light is zero. Only Einstein called it the speed of light. Especially because of the gamma ray bursters. See this: Firewall!
.
Swann’s paper is available here. I think the principle of equivalence is rather ambiguous. I wrote something about it in this article. The original principle of equivalence is not the principle of equivalence I read about in the popular press, or indeed in some papers.
.
The point I didn’t spell out was that in a tall tower, you can go down to the basement and see that the clock there is lagging behind the clock in the attic. This lag increases with time. Sorry, where was I talking about the ships decelerating? Harald was talking about that in his StackExchange question, I didn’t say much about it. I didn’t say it violates the equivalence principle did I?
.
I agree with most aspects of Einstein’s General Relativity. However I find myself disagreeing with many aspects of what you might call “Modern General Relativity”. It seems to be an ersatz version of the real thing, where the foundations have been disregarded, resulting in contradiction and paradox and error.
.
It’s good to hear you talking about energy conservation. I dislike it when people say things like “energy is not conserved in general relativity”. Matter is made of energy. It doesn’t just pop into existence. Or somehow fade away. Even in a place where space is “neither homogeneous nor isotropic”. I’m not fond of Noether’s theorem myself. Energy is what it is, and in a way it’s the only thing that is. Meanwhile, symmetry is abstraction.
.
I’m reading your paper. I scratched my head at this on page 2:“For topologies not readily mapped to a homogeneous space”. Because a gravitational field is inhomogeneous space. No matter. I like The coordinate velocity of light on page 3. And yes there are more momentum impulses per unit time on the bottom end of the rod. You shed energy when you descend, so the same force feels stronger, even though energy-momentum is conserved. But what’s this? Objects on a tether feel heavier at the bottom than the top? But they’ve lost mass! Your CFS postulate on pages 4 and 5 seems fine. You’re measuring the force of gravity in two different ways. I’m not sure about this on page 5 though: If temporal units are longer, then length units must be shorter and vice versa. We define the metre as the distance travelled by light in in 1⁄299792458 of a second. When light goes slower the second is bigger, but the metre doesn’t change. I’m not fond of page 6 I’m afraid. Like Newton, I view a gravitational field as a “pressure gradient in space”. Meanwhile space expands because of a “pressure in space”. Schrodinger called it cosmic pressure. On page 8 I liked this If a field imparts some kind of energy to objects or takes it from them It does this by converting internal kinetic energy, which is potential energy and mass-energy, into external kinetic energy. So I’m afraid I don’t like your equation 17. Because m varies. So does c. Sorry. I noticed this on page 12: If light had not been “double bent” by gravity. I think of matter as being half bent. The wave nature of matter means matter is akin to light in a closed path. Only the horizontal component curves down. All interesting stuff. Not as interesting as artificial gravity, eh? But that’s one for another day. Nice talking to you Robert!
I love how Michell said this, over a hundred years before Einstein: “concerning the diminution of the velocity of light in consequence of the attraction of the sun.”
Well said Anders. Thanks. Now why didn’t I say that in this post? I’m going to change the introduction to include it. I don’t like to change a post long after I’ve written it. However it’s only a minor addition, but very important. Thanks again.
God Almighty John. An answer of mine on Quora was just upvoted by Roy Kerr.
I just had to tell somebody… blown away.
Carry on!
Good man Anders! Hyperlink please!
I have sent you an email message.
Got it.
John, if a black hole, star, or any massive object had the gravitational gradients as you show in your image physicsdetective.com/wp-content/uploads/rubbersheetblackholes.png, I would think that the gravity gradient would tend to move things away from the center of the object and concentrate stuff in a hollow shell.
The math to model this is far beyond my abilities.
What is your opinion?
Don, that picture depicts gravitational potential between two stars. I probably mislabelled it by calling it rubbersheetblackholes.png. Probably because I copied some other drawing in a hurry. The equivalent depiction for a black hole has no gradient in potential inside the black hole. So there’s no gravity at all inside the event horizon. Like
, and like this:
“>
.
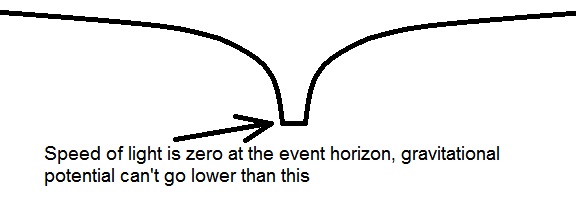Got it. Thanks John
John Duffield aka “Farsight” wrote above :
” but either way there’s something very small and very massive at the heart of our galaxy. We’re confident of this because of many years of work by many good men and women.”
.
My scale-invariant quantum antigravity hypothesis is very simple and clear, and it naturally explains what this: ” something very small and very massive at the heart of our galaxy” actually is. And it happens to be something that also eliminates the need for dark matter.
.
Galaxy rotation is the arena where the so-called “strong gravity” dominates.
.
My hypothesis clearly explains the principle of how the “strong gravity” is being generated by normal galactic dynamics, and therefore this: “something very small and very massive at the heart of our galaxy” is not massive at all, because it is (small) geometric center of the “strong gravity” being generated by the galaxy.
.
How could “strong gravity”, or any gravity at all, be possibly generated without anything massive, like black hole, or dark matter?
I have noticed that on this blog there have been some doubts expressed about the ultimate validity of mass-energy equivalence principle. Even if this principle is not as universal and unconditional as mainstream physics would like us to believe, for the sake of my argument I assume it to be good enough.
.
” Even masses at rest have an energy inherent to them. You’ve learned about all types of energies, including mechanical energy, chemical energy, electrical energy, as well as kinetic energy. These are all energies inherent to moving or reacting objects, and these forms of energy can be used to do work, such as run an engine, power a light bulb, or grind grain into flour. But even plain, old, regular mass at rest has energy inherent to it: a tremendous amount of energy. This carries with it a tremendous implication: that gravitation, which works between any two masses in the Universe in Newton’s picture, should also work based off of energy, which is equivalent to mass.” — Dr. Ethan Siegel, Ph.D., Astrophysicist
.
So, how could “strong gravity”, or any gravity at all, be possibly generated without anything massive, like black hole, or dark matter?
.
According to my hypothesis, the “strong gravity” is being generated from energy generated by normal galactic dynamics. However, it is not just any energy, but a specific, well-known form of energy.
.
All the details are explained in my paper and on my website, and most importantly, my hypothesis is easily and cheaply experimentally testable on a table’s top.
.
John, from the perspective of an outside observer, the concept of space and time breaks down inside the event horizon. So, it’s meaningless to talk about someone inside the event horizon shining a torch upwards. You’re extrapolating your spacetime experience on Earth with how things behave inside the event horizon.
For example, an outside observer can never see anything enter a black hole, because, from an external perspective, anything falling into a black hole slows down to almost zero. Not quite, as, to get to zero would take eternity, it cannot happen, eternity is a limit forever out of reach. So, if nothing can go in, from the outside world, then nothing can be seen coming out of it.
As for 4-D spacetime, iight, unlike massive particles, travels in geodesics. From the point of view of a photon, that photon gets from A to B instantly, there is no concept of the passage of time at all.
The Lorentz equations essentially a 4D spacetime fabric. Whereas Newton showed that the up-down dimenion is symmetric with left-right, forward-back, Einstein showed that the 4th dimension is symmetric with our 3D dimensions, except for a difference in sign.
The 4D picture agrees with experiment perfectly. So, it’s a reasonable picture. Saying that the speed of light changes because time slows down is equivalent. Light takes longer, from an external observer, to get from A to B, due to travelling on a geodesic that is, relative to us, curved. So, unless you can determine an experiment showing which interpretation of the mathematics is physicsl, then it’s just a metaphical argument.
Jim Eadon 30 Jun 2021 Reply
” So, unless you can determine an experiment showing which interpretation of the mathematics is physics, then it’s just a metaphical argument. ”
.
That is what I have always been saying to the likes of Dr. Jack Sarfatti :
Mathematics is not physics.
And mathematical physics is not experimental physics.
.
But the likes of Dr. Jack Sarfatti prefer to live in such a La-La Universe,
where all of the above is one and the same.
.
.
Jim: but it isn’t meaningless to extrapolate the upward light beam to a smaller denser body, until you get to a point where the light doesn’t get out. This isn’t meaningless either: “the curvature of light rays occurs only in spaces where the speed of light is spatially variable”. Nor is this: “This means that a clock kept at this place would go at the rate zero”. The same applies to the upward light beam. Its speed is zero, that’s why the black hole is black. Why do you think its black? Because gravity pulls the ascending light beam down? That’s wrong. In a gravitational field, the upward light beam speeds up.
.
Re the outside observer never seeing anything entering the black hole, no problem. See what Einstein said about light rays taking an infinitely long time to reach what we call the event horizon. That’s because at the event horizon, the speed of light is zero. Simple. However black holes do exist, so see my hailstone analogy. A water molecule can alight on the surface of the hailstone, but it can’t pass through the surface. However it can be surrounded and buried by other water molecules, so the surface can pass through it. That’s what the frozen-star black hole is all about.
.
As for 4-D spacetime, it models space at all times. So there is no motion in spacetime. So light doesn’t travel on a geodesics through spacetime. Yes, you can model the motion of light through space using spacetime, but make no mistake, the motion is through space, not spacetime, and the photon doesn’t get from A to B instantly. The 4D picture might agree with experiment perfectly, but the map is not the territory. Hard scientific evidence shows us that optical clocks go slower when they’re lower. So it’s not some metaphysical distinction. It cuts to the very heart of understanding Einstein’s general relativity, and why light curves – because space is inhomogeneous, wherein the speed of light is spatially variable. Saying light curves because it travels on a curved path through spacetime is throwing away that understanding and replacing it with a handwaving non-explanation that’s wrong on multiple counts, because there is no motion through spacetime, and spacetime curvature relates to the tidal force, not the “force” of gravity.
“Jim: … The same applies to the upward light beam. Its speed is zero, that’s why the black hole is black. Why do you think its black? Because gravity pulls the ascending light beam down? That’s wrong. In a gravitational field, the upward light beam speeds up.”
John, let me explain the “upward”-pointing lightbeam inside a black hole. Inside the black hole, the gravitational field is so intense that there is no geodesic (in this case, a geodesic being the shortest distance between two points in a “curved” 4D space-time) that light can follow that extends beyond the event horizon.
This explanation confounds our intuiton if you’re thinking in terms of our 3D-space experience, because, in our 3D experience shining a torch creates a beam in a straight line: the geodesic our intuition expects (the curvature of space is locally flat). In a black hole space is severely warped in 4D. If you’re not thinking in curved 4D, then you’re going to get extremely confused. Non-euclidian geometry is weird. Non-euclidian 4D geometry is even weirder.
“Re the outside observer never seeing anything entering the black hole, no problem. See what Einstein said about light rays taking an infinitely long time to reach what we call the event horizon. That’s because at the event horizon, the speed of light is zero.”
Be VERY careful before saying that. You’re getting yourself into all kinds of trouble. In the reference frame of someone crossing the event horizon, they see all light travelling at speed C. There is NO frame of reference where C is measured as equal to zero that can be experienced with finite energy, not unless you are a massless particle anyway. C is ALWAYS, and I mean ALWAYS measured as C.
“Simple. However black holes do exist, so see my hailstone analogy. A water molecule can alight on the surface of the hailstone, but it can’t pass through the surface. However it can be surrounded and buried by other water molecules, so the surface can pass through it. That’s what the frozen-star black hole is all about.”
John, that’s “simple”. And WRONG. The only reference frame where a “frozen-star black hole can exist, is the reference frame of an outside observer. In that referene frame, one sees matter falling towards, but never actualy into, the black hole.
“As for 4-D spacetime, it models space at all times. So there is no motion in spacetime. So light doesn’t travel on a geodesics through spacetime.”
A geodesic is the path, in 4D, taken by photons.
“Yes, you can model the motion of light through space using spacetime, but make no mistake, the motion is through space, not spacetime, and the photon doesn’t get from A to B instantly.”
Actually, from the reference frame of the photon itself, it does get from A to B instantly.
“Hard scientific evidence shows us that optical clocks go slower when they’re lower. So it’s not some metaphysical distinction.”
Yes it is.
“It cuts to the very heart of understanding Einstein’s general relativity, and why light curves – because space is inhomogeneous, wherein the speed of light is spatially variable.”
To get that to work, you need “speed of time” to “slow down” – ugly! Also, it’s just philosophy. You’re just trying to interpret the equations in one way, instead of another, more natural, way. You’re trying to bend spacetime by bending it in the “time” axis. Worse, you can give me no experiment that can show that what you are saying is even meaningful as physics.
“Saying light curves because it travels on a curved path through spacetime is throwing away that understanding and replacing it with a handwaving non-explanation that’s wrong on multiple counts, because there is no motion through spacetime, and spacetime curvature relates to the tidal force, not the “force” of gravity.”
John, this is hypocrisy, a hypocritical philosophy. You’re just bending spacetime in the time-direction, then claiming that it means C varies. Which is just a handwaving non-explanation. You’re just a philosopher trying to mash up the GR equations in one way instead of in another way. The thing is, you make erronous statements about black holes and “time stopping” along the way, which is a red flag.
An analogy.
Let’s say you’re in “flat land”. You’re a 2D flat person, and and you’re in a black hole, the event horizon of which is a flat circle. You are inside that circle in the x-y plane. You shine a torch “upwards” to the “top” of the circle, along the y-axis, the circle being the event horizon. You see the light move away from you in a straight line – at first. It moves up the y-axis towards the boundary circle. But then what happens is, the light goes into the z-axis, and, in the z-axis, it curves away from your flat-land. Ultimately it goes around until, relative to the y-axis, it starts to go “backwards”. You do not see the z-plane, so, to you, the light goes up in the y-axis, then down again, in the y-axis.
It’s as if the light is following a geodesic like the circumpherence of another circle, in the y-z plane, that arcs out of your flat x-y land. The z-dimension is curved, which is why the light moves in a circle relative to the flat-land.
This is what 4D does to 3D inside a black hole event horizon. It can move a beam of light away from the event horizon, because it’s following a “straight line” in a curved 4D space. All straight lines curve away from the event horizon. Because curved space bends lines that are still the shortest distance between two points.
Jim, that is abject handwaving. Let me reiterate: there is no motion in spacetime. Light does not move in 4D spacetime. Google on there is no motion in spacetime. Your “explanation” is popscience nonsense that flatly contradicts Einstein’s general relativity. Here’s what Einstein said: “As a simple geometric consideration shows, the curvature of light rays occurs only in spaces where the speed of light is spatially variable”. He also said “This means that a clock kept at this place would go at the rate zero. Further it is easy to show that both light rays and material particles take an infinitely long time (measured in “coordinate time”) in order to reach the point r = μ/2”. You’ve already said this:
.
“For example, an outside observer can never see anything enter a black hole, because, from an external perspective, anything falling into a black hole slows down to almost zero. Not quite, as, to get to zero would take eternity, it cannot happen, eternity is a limit forever out of reach. So, if nothing can go in, from the outside world, then nothing can be seen coming out of it.”.
.
That nearly matches what Einstein said. But now you’ve totally changed tack, and you’re flatly contradicting Einstein. That means the general relativity you think you know isn’t general relativity. Which isn’t surprising, since it’s peddled by the likes of Kip Thorne, who will tell you that a black hole is a time-machine tesseract wormhole that leads back to your bookcase.
“a metaphical argument.”
*metaphysical.
Furthermore, the idea of time slowing down is not all that satisfying anyway. We know that the 3D world is spacial, and we know that time seems dimension like, so we’re dealing with a 4D world, where any point at any moment is described by 4 coordinates. To discuss that 4D world as containing curvature, similar to the curvature of the surface of the world, is, to me, more satisfying than the rather awkward explanation of “time slowing down”. How many seconds per second is time slowing down? At what rate is time “running” anyway?
Jim Eadon 30 Jun 2021 Reply
” At what rate is time “running” anyway? ”
.
In GTR, “time” is the 4th stationary dimension of stationary space.
This being the only reason why in GTR you can travel in time,
in theory only, of course. Exactly, like Dr. Jack Sarfatti does it
in his pseudo-scientific theoretical propaganda videos.
.
.
I didn’t say time slows down. I said light slows down. It’s that simple. Don’t overthink it. Read my article on the nature of time. Time is merely a cumulative measure of local motion. It isn’t something you can move through. Once you know this, you know that when Kip Thorne waxes lyrical about time travel, he is talking out of his arse. You might find it satisfying to think that gravity is due to a 4D world containing curvature, but you shouldn’t, because you’re confusing the abstract mathematical model with reality. We live in a world of space and motion. Not in some 4D block universe comprised of space at all times. Which is therefore totally static. Google on there is no motion in spacetime.
C is constant, so, therefore “time” must be warped (“slowed down” to slow down “C”. The reason? Any observer measuring C always measures it as exactly C.
No, c is not constant. Optical clocks go slower when they’re lower. Because light goes slower when it’s lower. Just like Einstein said:
.
1912: “On the other hand I am of the view that the principle of the constancy of the velocity of light can be maintained only insofar as one restricts oneself to spatio-temporal regions of constant gravitational potential”.
.
1913: “I arrived at the result that the velocity of light is not to be regarded as independent of the gravitational potential. Thus the principle of the constancy of the velocity of light is incompatible with the equivalence hypothesis”.
.
1914: “In the case where we drop the postulate of the constancy of the velocity of light, there exists, a priori, no privileged coordinate systems.”
.
1915: “the writer of these lines is of the opinion that the theory of relativity is still in need of generalization, in the sense that the principle of the constancy of the velocity of light is to be abandoned”.
.
1916: “In the second place our result shows that, according to the general theory of relativity, the law of the constancy of the velocity of light in vacuo, which constitutes one of the two fundamental assumptions in the special theory of relativity and to which we have already frequently referred, cannot claim any unlimited validity”.
.
1920: “Second, this consequence shows that the law of the constancy of the speed of light no longer holds, according to the general theory of relativity, in spaces that have gravitational fields. As a simple geometric consideration shows, the curvature of light rays occurs only in spaces where the speed of light is spatially variable”.
.
As I’ve said before, what you’ve been taught flatly contradicts Einstein, so it isn’t general relativity. An observer always measures the local speed of light to be the same because he uses the local motion of light to define his metres and his seconds. Then he uses them to measure the local motion of light. Duh! That’s the tautology. I talked about it in https://physicsdetective.com/the-speed-of-light/, see https://arxiv.org/abs/0705.4507.
In fact, with time being a coordinate, the concept of time “slowing down” – (which is tautological, you measure how much something slows down using time) would lead to a “curved” spacetime anyway, in terms of how you would describe any point in physical space at any moment, and plot such points. So, back to square one.
If you’re going to play god, and say Einstein was right about this, but wrong about that, prove it. Go ahead and prove it with a mathematical law of physics that contradicts the Einstein equations. Otherwise, it’s just blah blah blah, much ado about nothing. You’re not doing physics, you’re doing philosophy.
Jim: the evidence proved it. Irwin Shapiro used that evidence to prove it. See Wikipedia and take note of this: “Because, according to the general theory, the speed of a light wave depends on the strength of the gravitational potential along its path…” So the theory you were taught, which says the speed of a light wave doesn’t depend on gravitational potential, is not general relativity. By the way, I referred to Irwin Shapiro in the article above. You haven’t even read this article, have you? Have you read any of them?. Methinks the answer is no, because you think you know better. So much so that you haven’t even looked at the Einstein digital papers. It’s called hubris, Jim. Intellectual arrogance. I am reminded of the quote from Avatar: “It is hard to fill a cup that is already full”. I am also reminded of Alexander Unzicker, who said we should stop all physics funding, because it’s getting in the way of scientific progress.
AMEN John !
Jim: the evidence proved it. Irwin Shapiro used that evidence to prove it. See Wikipedia and take note of this: “Because, according to the general theory, the speed of a light wave depends on the strength of the gravitational potential along its path…”
John, this depends on reference frame. Also, in addition, light “slows” in any material or energy field, because the photons are being destroyed, and recreated by that material / energy field. The photons themselves are ALWAYS moving at exactly C. You fail to make this distinction, and so you make sloppy statements that are misleading.
“So the theory you were taught, which says the speed of a light wave doesn’t depend on gravitational potential, is not general relativity.”
See my comment above.
“By the way, I referred to Irwin Shapiro in the article above. You haven’t even read this article, have you? Have you read any of them?”
John, I have a degree in this stuff. You don’t.
“Methinks the answer is no, because you think you know better.”
No I do not, you’re attacking a strawman. Again refer to my comment above.
“So much so that you haven’t even looked at the Einstein digital papers. It’s called hubris, Jim. Intellectual arrogance.”
Ha ha ha oh the irony! How self-unaware is our physics “detective”. John, once you stop saying imprecise, misleading or worse, statements about GR, THEN you can lecture me. Please learn the difference between the “speed of a light beam travelling through a medium, vs what C is. This is fundamental stuff, and you conflate the two, like uneducated amateurs are wont to do.
No, it doesn’t depend on the reference frame. Because a reference frame is an abstract thing that doesn’t actually exist. I can point up to the clear night sky and show you the Moon, or a star, or a laser beam. But you cannot show me a reference frame. Do not elevate abstract mathematical concepts that do not exist, above the things that do. Space exists, and light exists, as does the motion of that light through space. But a reference frame does not. It’s like what I was saying about spacetime: the map is not the territory.
.
No, photons are not being destroyed as they move through space. You are winging it again, and making up hand-waving fairy tales to fit your conviction, which doesn’t match the hard scientific evidence. See my previous comment. Photons move slower when they’re lower. Just like Shapiro proved. Just like Einstein said. Repeatedly, year after year after year: the curvature of light rays occurs only in spaces where the speed of light is spatially variable. When it comes to general relativity, you think you know better than Shapiro and Einstein, don’t you? I’ve got news for you: you don’t.
.
As for I have a degree in this stuff, I’ve spent far far longer researching this “stuff” than you. And I’ve got it from the horse’s mouth. Not third-hand parrot-fashion in some academic madrasa from some quack who contradicts Einstein whilst peddling nonsense about worm holes and time travel back to your book case. I’m not just some uneducated amateur. Because I’m with Einstein and the evidence, and you’re not. Sorry Jim, but when it comes to GR, your “education” is miseducation. Take a look at Misconceptions in gravitational physics to understand just how wrong your education is. Then do yourself a favour. Stand in front of your bathroom mirror, and repeat after me: “Everything I think I know about general relativity flatly contradicts Einstein and the evidence, and therefore is flat out wrong”. The penny will drop eventually, and you’ll be a better man for it. Then you will understand this: Do your own research and think for yourself.
JD “No, it doesn’t depend on the reference frame. Because a reference frame is an abstract thing that doesn’t actually exist. I can point up to the clear night sky and show you the Moon, or a star, or a laser beam. But you cannot show me a reference frame. Do not elevate abstract mathematical concepts that do not exist, above the things that do. Space exists, and light exists, as does the motion of that light through space. But a reference frame does not. It’s like what I was saying about spacetime: the map is not the territory.”
John, a reference frame is as “real” (this question is sounding like metaphysics, not physics) as any other aspect of the equations (“space”, “light” or whatever). Loosely speaking, It’s the state of the observer. If you do not know the state of the observer, then you cannot solve the equations regarding what is seen (or not seen) for typical physics problems. Because the equations give different answers for different observers, depending on their location and velocity (SR) and the local gravitational field and accelleration (GR).
JD “No, photons are not being destroyed as they move through space. You are winging it again, and making up hand-waving fairy tales to fit your conviction, which doesn’t match the hard scientific evidence.”
John, are you actually claiming that the Dirac Equation, and the standard model (a Quantum Field Theory) are wrong? Fascinating, gtiven they describe experiments to more than a dozen decimal places. I hope you have a proof of your wild claim, and win a nobel prize. There’s only one fellow “winging it” here, and it’s the guy without a physics degree.
JD “Photons move slower when they’re lower. Just like Shapiro proved.”
WRONG. Photons actually move at C. What is really happening is, a beam of light moves more slowly through an energy field than through a vaccuum. (In a pure, energy-field-free vaccume, there is nothing to absorb and re-emmit photons). But photons always move at the constant “C”. The slow-down of beam of light is entirely due to field interactions destroying, and, after a delay, re-emmitting photons. When the light arrives after passing through a medium or field, it’s not the same photons coming out as went in. See Dirac’s equation for details. I take your Einstein and raise you Dirac.
JD “Just like Einstein said. Repeatedly, year after year after year: the curvature of light rays”
John, see my comment about photons being absorbed and re-emmitted by energy and matter fields.
JD “When it comes to general relativity, you think you know better than Shapiro and Einstein, don’t you? I’ve got news for you: you don’t.”
John, you’re so high and mighty, aren’t you? Well, “detective”, I’ve got news for you. Your mistake is in interpreting what these men are saying about the equations. Observe ANY individual photon, and you’ll see it moving at C, the constant that is the speed of light in a vaccuum. Individual photons cannot “slow down”. Massless particles must move at C. Again, consider the reference frame, this time, of the photon. From such a reference frame, time does not exist at all. So, it cannot “slow down”, or you just gave it mass in effect. Which is impossible, at least for known physics.
JD “As for I have a degree in this stuff, I’ve spent far far longer researching this “stuff” than you”
John, the problem with this is, you do not have the correct scientific training to make sense of the equations. You’re just reading words, which are imperfect descriptions of the equations. And then you add 2 and 2 and declare it’s 3, because the 2’s “slow down”. Not so, because “2” is a constant.
“I’m not just some uneducated amateur. Because I’m with Einstein and the evidence, and you’re not. Sorry Jim, but when it comes to GR, your “education” is miseducation. Take a look at Misconceptions in gravitational physics to understand just how wrong your education is. Then do yourself a favour. Stand in front of your bathroom mirror, and repeat after me: “Everything I think I know about general relativity flatly contradicts Einstein and the evidence, and therefore is flat out wrong”. The penny will drop eventually, and you’ll be a better man for it. Then you will understand this: Do your own research and think for yourself.”
John, that’s a self-indulgent fantasy of the physics-uneducated amateur. You have no physics degree, you should show more humility, you’re inexpert.
In conclusion, let me say that you are using language in imprecise ways, and consequently, you’re making incorrect statements about the science by pushing things too far, mixing up different concepts, ignoring fundamental entities, such as reference frames, etc. You make claims like “a reference frame does not exist”. That’s a red flag right there! You throw reference frames in the bin, when “reference frames” are the heart, the “relativity” in SR and GR. When such garbage is written, and that is only one various bizarre examples, then one can rest assured that the writer does not understand the even the basic basics of SR and GR. This is an simply a salient case of Dunning Kruger syndrome.
Jim: no, a reference frame is not real. Nor is a world line, nor is a light cone. Whilst you might say that a reference frame is “the state of the observer”, that doesn’t change what’s there. For example, a black hole is a place where the speed of light is zero. That’s why it’s black. If you put an observer at that location, the speed of light is still zero at that location. It doesn’t change to 299,792,458 m/s. You might claim that “in his reference frame” that observer sees the speed of light at that location to be 299,792,458 m/s. He doesn’t. It’s a schoolboy error to think he does. The speed of light at that location is zero. So he sees nothing. Ever.
.
Re: John, are you actually claiming that the Dirac Equation, and the standard model (a Quantum Field Theory) are wrong? Fascinating, given they describe experiments to more than a dozen decimal places. I hope you have a proof of your wild claim, and win a Nobel prize. There’s only one fellow “winging it” here, and it’s the guy without a physics degree. I’m not winging it. Photons are not being destroyed and recreated as they move through space. See the black hole charlatans where you can read Svend Rugh and Henrik Zinkernagel’s 2002 paper on the quantum vacuum and the cosmological constant problem. They point out that photons do not scatter on the vacuum fluctuations of QED, saying that if they did, “astronomy based on the observation of electromagnetic light from distant astrophysical objects would be impossible”. Hence the QED vacuum energy concept is “an artefact of the formalism with no physical existence independent of material systems” Also read Something is rotten in the state of QED. Oliver Consa has investigated the claims that QED is the most accurate theory ever, and tells of theoreticians constantly changed their “predictions” to match experimental results. it’s scientific fraud, Jim. Sorry.
.
Re WRONG. Photons actually move at C. What is really happening is, a beam of light moves more slowly through an energy field than through a vaccuum. (In a pure, energy-field-free vacuum, there is nothing to absorb and re-emit photons). But photons always move at the constant “C”. The slow-down of beam of light is entirely due to field interactions destroying, and, after a delay, re-emitting photons. This simply isn’t true. You’re making things up to cling to conviction, and you’re contradicting Einstein, Shapiro, and the hard scientific evidence.
.
Re: John, you’re so high and mighty, aren’t you? Well, “detective”, I’ve got news for you. Your mistake is in interpreting what these men are saying about the equations. Observe ANY individual photon, and you’ll see it moving at C, the constant that is the speed of light in a vacuum. Individual photons cannot “slow down”. Massless particles must move at C. Again, consider the reference frame, this time, of the photon. From such a reference frame, time does not exist at all. So, it cannot “slow down”, or you just gave it mass in effect. Which is impossible, at least for known physics. As above. There is no way to misinterpret “the speed of light is spatially variable” or “the speed of a light wave depends on the strength of the gravitational potential”.
.
Re: John, the problem with this is, you do not have the correct scientific training to make sense of the equations. You’re just reading words, which are imperfect descriptions of the equations. And then you add 2 and 2 and declare it’s 3, because the 2’s “slow down”. Not so, because “2” is a constant. Your arrogance knows no bounds. I’m not the only one saying this. See The Speed of Light Everywhere the Same? by PhysicsFAQ editor Don Koks. The answer is no. Note this: “light speeds up as it ascends from floor to ceiling, and it slows down as it descends from ceiling to floor; it’s not like a ball that slows on the way up and goes faster on the way down. Light travels faster near the ceiling than near the floor. But where you are, you always measure it to travel at c; no matter where you place yourself, the mechanism that runs the clock you’re using to measure the light’s speed will speed up or slow down precisely in step with what the light is doing. If you’re fixed to the ceiling, you measure light that is right next to you to travel at c. And if you’re fixed to the floor, you measure light that is right next to you to travel at c. But if you are on the floor, you maintain that light travels faster than c near the ceiling. And if you’re on the ceiling, you maintain that light travels slower than c near the floor.”
.
Re: John, that’s a self-indulgent fantasy of the physics-uneducated amateur. You have no physics degree, you should show more humility, you’re inexpert. I know far more about this subject than you. I’m not showing humility to some guy who peddles the Kip Thorne pseudoscience that flatly contradicts Einstein, Shapiro, and the hard scientific evidence.
.
Re: In conclusion, let me say that you are using language in imprecise ways, and consequently, you’re making incorrect statements about the science by pushing things too far, mixing up different concepts, ignoring fundamental entities, such as reference frames, etc. It all starts with understanding one simple little thing. Here’s those quotes again: “the speed of light is spatially variable” or “the speed of a light wave depends on the strength of the gravitational potential”.
.
Re: You make claims like “a reference frame does not exist”. It doesn’t. That’s why you can’t show me one. It isn’t a fundamental entity at all. It’s a mathematical abstraction.
.
Re: That’s a red flag right there! You throw reference frames in the bin, when “reference frames” are the heart, the “relativity” in SR and GR. When such garbage is written, and that is only one various bizarre examples, then one can rest assured that the writer does not understand the even the basic basics of SR and GR. This is an simply a salient case of Dunning] Kruger syndrome. No it isn’t. Because I’m with Einstein, whilst you are not.
.
Edit 04/07/2021: Jim, whilst I’m all for free speech in science, you have overstepped the mark, and I have removed your latest abusive comments. End of conversation.
JD – “Jim: no, a reference frame is not real. Nor is a world line, nor is a light cone. Whilst you might say that a reference frame is “the state of the observer”, that doesn’t change what’s there.”
John, Regarding reference frames, if you are saying that the states of the observer, which I described, are not real, then you’re wrong. Observers have properties, attributes and states that are fundamental to SR and GR calculations. As I say, you do not even have a basic understanding.
JD “For example, a black hole is a place where the speed of light is zero.”
WRONG. Refer to my previous answers on this, I’m not going to repeat myself.
JD “That’s why it’s black.”
That does not explain why they are “black”, and, besides, blackholes do emit radiation, if Hawking’s theory is correct.
JD “If you put an observer at that location, the speed of light is still zero at that location.”
See my previous refutaiton to this myth.
“Photons are not being destroyed and recreated as they move through space.”
Yes, they are. I refer you to my previous explanation.
JD “See the black hole charlatans where you can read Svend Rugh and Henrik Zinkernagel’s 2002 paper on the quantum vacuum and the cosmological constant problem. They point out that photons do not scatter on the vacuum fluctuations of QED, saying that if they did, “astronomy based on the observation of electromagnetic light from distant astrophysical objects would be impossible”.
John, that a huge red herring. The cosmological constant problem is nothing to do with it. The CC is non-zero, and therefore photon absorbion and re-emmision occurs, obeying the Dirac equation.
“Hence the QED vacuum energy concept is “an artefact of the formalism with no physical existence independent of material systems” Also read Something is rotten in the state of QED. Oliver Consa has investigated the claims that QED is the most accurate theory ever, and tells of theoreticians constantly changed their “predictions” to match experimental results. it’s scientific fraud Jim Sorry.”
John, this is, shall we say, iffy. I’ve never heard of anyone in science is discussing the the issue this guy has raised. Red herring, red flag. In general, phycists surmise that QM is more fundamental than Relativity, and, they believe that Relativity is an approximation to a quantum field theory (quantum gravity).
JD “You’re making it up, you’re clutching at straws to cling to conviction, and you’re contradicting Einstein, Shapiro, and the hard scientific evidence.”
John,. that’s a nice bit of projection of your own faults. I’m not contradicting Einstein, nor Shapiro. I’m simply explaining them to you, who misunderstands the science, and says bullshit nonsense about it.
“There is no way to misinterpret “the speed of light is spatially variable” or “the speed of a light wave depends on the strength of the gravitational potential”.
Again, you confuse the speed of light through a medium with the constant “C”. No matter how often I point this out, you still get confused about it.
“No it isn’t. Because I’m with Einstein, whilst you are not.”
Keep kidding yourself. You’re an uneducated fellow, with zero scientific training, who cannot eventell the difference between the “speed of light” through a medium, such as an energy field, such as a gravitational field, or even the quantum vaccuum energy, and the constant “C” from E=MC^2. Seriously John, you are simply embarrassing yourself with your schoolboy errors. Many of which I have pointed out. You’re one of those men who thinks he understand modern physics using his intuition, instead of understanding the mathematics. Bad mistake.
I would like to make one more remark about the Einstein equations. For certain inputs, the equations give absurd answers. One of those absurd answers is the “singularity”, where matter is infinitely dense, squashed into a mathematical point. Physicists believe that this does not really happen. That, a new theory, quantum gravity, as yet undiscovered, will take over before that happens, showing that the singularity would not come into physical existence.
On a more subtle level, the “time stops here” solution to the GR equations also makes no physical sense. You cannot stop a massless boson, it’s as simple as that. To the physically and mathematically naive amateur, they see nothing wrong with that, when they should. So, how do we understand the Time-Stops solution? The answer is, you have to consider it a “limit”, analogous to considering infinities in calculus as “limits”, not actual (because the mathematics breaks down for calculus at infinity).
OK, so Time Stops is a limit. Next we turn to reference frames. From the POV of someone falling into the black hole, then time never stops, even though they cross the event horizon. That’s what the equations say. It’s only for an outside observer that the GR equations say Time can be zero. But, again, this is a limit, and it’s not physical. It NEVER happens. Photons always travel at C. As I explained before, from the outside reference frame. one sees matter approaching the event horizon, but NEVER reaching it. To get to the time stops limit, you would have to observe what happens for ETERNITY. (Besides, quantum graviational effects would probably prevent time “stopping” even then!).
So, John, your approach to GR is mathematically and physically naive. Beware using your layman’s intuition when it comes to modern physics!
Jim: say you trap a photon in a gedanken mirror box. That obviously doesn’t stop it, it keeps travelling back and forth at c. (Let’s disregard the fact that an outside observer will never detect it, which may or may not have relevance to the discussion of black holes.) But if we now move the mirrors closer until the distance between them is zero in the limit (or let’s say a Planck length to keep it physical) – does the photon actually cover a distance, even in its own reference frame?
.
Another point to ponder is the meaning of c. It is the velocity of light so by definition it is the only speed light will propagate at. But what if the meter is infinitely contracted and the second lasts an infinite amount of time? Is that not effectively “stopped”, i.e. zero speed?
If I can volunteer an answer, Anders:
.
I think the standing-wave photon is still moving at c. If it didn’t, the electron wouldn’t fall down, and charged particles wouldn’t move towards one another, or away from one another, or around one another. I say that because I think that the Williamson / van der Mark electron model, which says the electron is a double-wrapped photon, is right. What was a sinusoidal field variation now looks like a standing field, but it isn’t actually standing. See What charge is.
.
IMHO when the meter is infinitely contracted and the second is infinite, then yes, light is stopped. I think this is the situation at the black hole event horizon, and that’s why the black hole is black.
Jim Eadon 30 Jun 2021 Reply
” Otherwise, it’s just blah blah blah, much ado about nothing. You’re not doing physics, you’re doing philosophy. ”
.
Jim, please, do not insult philosophy.
.
You can call it a pseudo-scientific fantasy.
.
As a highest honor, Enstein was called : a Philosopher-Scientist :
.
https://www.amazon.com/Albert-Einstein-Philosopher-Scientist-Library-Philosophers/dp/0875481337
.
.
Hi Ziggy,
I wasn’t particularly denigrating philosophy. Einstein was a philosopher about Quantum Mechanics, but it turned out that Quantum Mechanics did not like his philosophy. Not one bit…
And that’s the problem for philosophy. 3000 years of thinkers failed to predict quantum mechanics. Newton was way ahead of his time, when science was “natural philosophy”, he practically invented physics.
Clifford, a British mathematician (inventor of the important Clifford Algebra), anticipated relativity about 30 years(?) before Einstein, describing how he thought cosmological physics would evolve along geometric lines. He was precient. Lorentz invented the mathematical equation of special relativity (a non-euclidian geometry basically) but failed to apply it to the real world, and become a celeb.
Those are the great thinkers of history, guys like that.
Black Holes & Curved SpaceTime
Most stars end their lives as white dwarfs or neutron stars. When a very massive star collapses at the end of its life, however, not even the mutual repulsion between densely packed neutrons can support the core against its own weight. If the remaining mass of the star’s core is more than about three times that of the Sun (MSun
), our theories predict that no known force can stop it from collapsing forever! Gravity simply overwhelms all other forces and crushes the core until it occupies an infinitely small volume. A star in which this occurs may become one of the strangest objects ever predicted by theory—a black hole.
for more info, go to :
https://quantxcer.com/display-high-energy-physics-news.php?file-name=high-energy-physics/black-holes-curved-spacetime
Pavan, I would urge you to read the Einstein digital papers, and then you will hopefully get an idea of how gravity works. A gravitational field is a place where the speed of light varies. At the black hole event horizon, the speed of light is zero, and it can’t go lower than that. Since there’s no local gradient in the speed of light, there’s no gravitational field, and so no more collapse.
https://www.inverse.com/science/novel-experiment-map-space-time-black-hole-movie-physicists
This link has a fascinating collection of the controversial computer enhanced photos/videos of black holes. Most of the explanations are SM based bollocks and the tired old “gravity curves space-time” argument of course. Also, the author doesn’t seem to have grasp that the entire universe is moving constantly and not static. Yes indeed, the map is not the country.
But look at all those beautiful vortices in each and every photo ! Everything appears to be in a constant state of rotation. Too bad they haven’t read Dr. Bernard Schaeffer, or about Quantum Knot theories, just for starts.